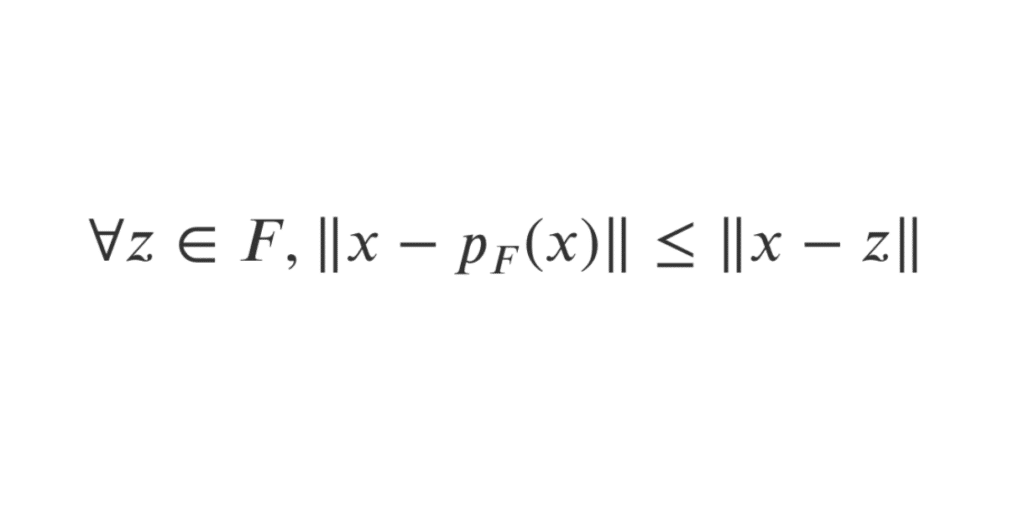Les notions hors programme se destinent surtout aux candidats qui visent les trois Parisiennes. Cet article te propose de décortiquer le théorème de caractérisation par minimisation de la norme et d’en comprendre une de ses utilisations, le problème des moindres carrés, assez récurrent dans les sujets de concours, pour mieux t’aider à comprendre comment trouver des pseudo-solutions d’un système qui n’a pas de solution.
Le théorème de caractérisation par minimisation de la norme est au programme de maths approfondies (attention, seulement le théorème, les pseudo-solutions n’y sont pas). En revanche, il n’est pas au programme de maths appliquées.
Théorème de caractérisation par minimisation de la norme
\(F\) est un sous-espace vectoriel d’un espace euclidien \(E\) et \(p_{F}\) est la projection orthogonale sur \(F\).
Soit \(x\) un élément de \(E\) :
\(\forall z\in F,\|x-p_{F}(x)\|\le\|x-z\|\) avec égalité si et seulement si \(z=p_{F}(x)\).
Autrement dit, \(\|x-p_{F}(x)\|\) est le minimum de l’ensemble {\(\|x-z\|,z\in{F}\)} et \(p_{F}(x)\) est l’unique élément de \(F\) qui réalise ce minimum.
La projection orthogonale de \(x\) sur \(F\) est la meilleure approximation de \(x\) par un élément de \(F\).
Démonstration
Soit \(x\in E\), soit \(y\in E\).
On sait que
\(p_{F}+p_{F^\perp}=\text{id}_{E}\), ainsi \(p_{F}(x)+p_{F^\perp}(x)=x\).
On a donc : \(\|x-z\|^2=\|p_{F}(x)-z+p_{F^\perp}(x)\|^2\).
Or, on a \((p_{F}(x)-z)\in F\) et \(p_{F^\perp}(x)\in F^\perp\).
On peut donc séparer, d’après le théorème de Pythagore et :
\(\begin{align}\|x-z\|^2&=\|p_{F}(x)-z\|^2+\|p_{F^\perp}(x)\|^2\\&=\|p_{F}(x)-z\|^2+\|x-p_{F}(x)\|^2\end{align}\)
Or, \(\|p_{F}(x)-z\|^2\ge0\) avec égalité si et seulement si \(p_{F}(x)=z\).
Ce qui donne alors que :
\(\forall z\in F,\|x-p_{F}(x)\|^2\le\|x-z\|^2\) avec égalité si et seulement si \(z=p_{F}(x)\).
En passant à la racine carrée (fonction croissante sur \(\mathbb{R}^{+}\)), on a donc finalement que :
\(\forall z\in F,\|x-p_{F}(x)\|\le\|x-z\|\) avec égalité si et seulement si \(z=p_{F}(x)\).
Remarque importante
Ce théorème vaut encore dans un espace préhilbertien réel \(E\) pourvu que \(F \oplus F^\perp=E\). Rappelle-toi que c’est le cas lorsque \(F\) est de dimension finie. D’où l’importance de connaître la démonstration que les concepteurs recyclent souvent lorsqu’ils souhaitent te faire travailler dans des espaces préhilbertiens réels quelconques.
Une utilisation de ce théorème : le problème des moindres carrés
Quand un système linéaire de la forme \(
\begin{cases}
a_{1,1}x_1+…+a_{1,p}=b_1\\
a_{2,1}x_1+…+a_{2,p}=b_2\\
…\\
a_{n,1}x_1+…+a_{n,p}=b_n\\
\end{cases}
\) n’admet pas de solution, on peut déterminer une pseudo-solution.
Il faut alors déterminer le ou les valeurs de \(x_1,x_2,…,x_p\) qui rendent minimale une somme de \(n\) carrés :
\(\begin{align}S&=(a_{1,1}x_1+…+a_{1,p}-b_1)^2+…+(a_{n,1}x_1+…+a_{n,p}-b_n)^2\\&=\displaystyle \sum_{i=1}^{n}(\displaystyle \sum_{j=1}^{p
}a_{i,j}x_j-b_i)^2\end{align}\)
Un exemple de résolution d’un problème
Soit \(S\) le système : \(
\begin{cases}
x+2y=1\\
x+y=1\\
x-y=-1\\
\end{cases}
\)
On vérifie facilement que \(S\) n’admet pas de solution. On peut alors chercher une pseudo-solution au système par la méthode des moindres carrés en cherchant :
\(\displaystyle \min_{(x,y)\in{\mathbb{R}^2}}(x+2y-1)^2+(x+y-1)^2+(x-y+1)^2\).
On pose :
\(u_1=(1,1,1)
u_2=(2,1,-1)
v=(1,1,-1)\).
On a donc :
\(xu_1+yu_2-v=(x+2y-1,x+y-1,x-y+1)\)
et ainsi :
\(\|xu_1+yu_2-v\|^2=(x+2y-1)^2+(x+y-1)^2+(x-y+1)^2\).
Ainsi :
\(\displaystyle \min_{(x,y)\in{\mathbb{R}^2}}\|xu_1+yu_2-v\|^2=\min_{w\in{vect(u_1,u_2)}}\|w-v|^2\).
On cherche donc désormais le minimum d’une norme, ce qui nous rapproche du théorème de caractérisation par minimisation de la norme.
On pose maintenant \(E=\mathbb{R}^{3}\) et son sous-espace vectoriel euclidien \(F=vect(u_1,u_2)\) (espaces euclidiens, car de dimension finie).
D’après le théorème de caractérisation par minimisation de la norme, le minimum cherché est trouvé quand \(w=p_F(v)\).
Ici, \(F\) est de dimension 2 et sous-espace vectoriel d’un espace de dimension 3, ainsi \(F^\perp\) est de dimension 1. On cherche donc la projection orthogonale sur \(F^\perp\) qui sera plus facile à trouver que celle sur \(F\), car la dimension est inférieure, puis on utilisera le fait que \(p_{F}+p_{F^\perp}=\text{id}_{E}\).
Explicitons alors \(F^\perp\) :
\(\begin{align}\forall t=(x,y,z)\in&{F^\perp},\begin{cases}
\langle t,u_1\rangle=0\\
\langle t,u_2\rangle=0\\
\end{cases}\\&\Leftrightarrow
\begin{cases}
x+y+z=0\\
2x+y-z=1\\
\end{cases}\\&\Leftrightarrow
\begin{cases}
x=2z\\
y=-3z\\
\end{cases}\\&\Leftrightarrow F^\perp=vect((2,-3,1)) \end{align}\).
On a
\((e=\frac{1}{\sqrt{14}}(2,-3,1))\) est une base orthonormée de \(F^\perp\) et ainsi, on peut calculer \(p_{F^\perp}(v)=\langle v,e\rangle e=\frac{1}{14}*(-2)*(2,-3,1)=\frac{-1}{7}(2,-3,1)\).
Ainsi,
\(p_F(v)=v-p_{F^\perp}(v)=\frac{1}{7}(9,4,-6)\).
On a donc finalement que la pseudo-solution du système de départ est \(x\) et \(y\) tels que \(xu_1+yu_2=\frac{1}{7}(9,4,-6)\).
C’est-à-dire \(\begin{cases}
x+2y=\frac{9}{7}\\
x+y=\frac{4}{7}\\
x-y=\frac{-6}{7}
\end{cases}\Leftrightarrow
\begin{cases}
x=\frac{-1}{7}\\
y=\frac{5}{7}\\
\end{cases}\).
Remarque
Cette méthode peut paraître longue et fastidieuse, mais c’est toujours la même, il est donc utile de la connaître. Une fois maîtrisée, elle ne pose aucun problème, tant que tu ne te trompes pas dans les systèmes intermédiaires.
N’hésite pas à consulter toutes nos ressources de mathématiques !