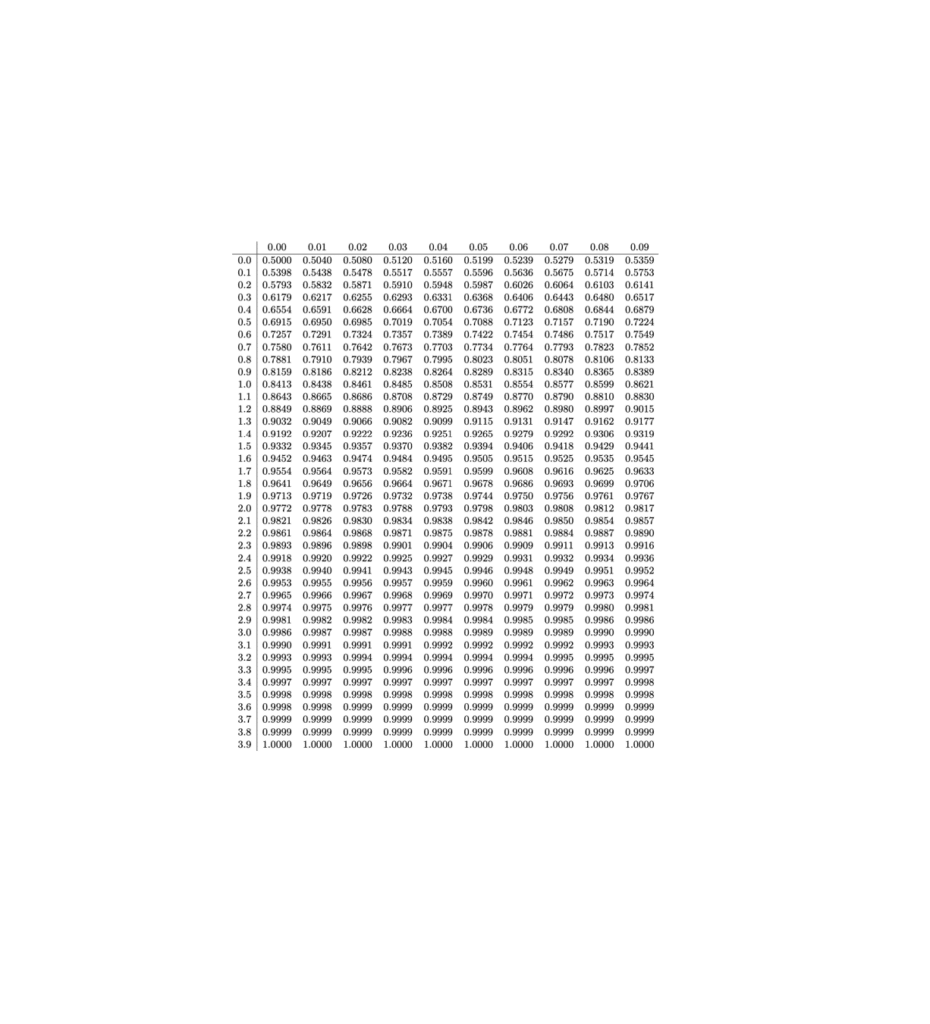La loi centrée réduite \(\mathcal{N}(0,1) \) a pour densité \( \phi : t \mapsto \frac{1}{\sqrt{2\pi}} e^{\frac{-t^2}{2}}\) . Il est impossible de trouver une primitive de \( \phi \) à l’aide des fonctions au programme, et il est donc impossible de déterminer la fonction de répartition d’une variable aléatoire \(X\) autrement qu’à l’aide d’une intégrale si \( X \hookrightarrow \mathcal{N}(0,1) \) . Ainsi, pour donner une valeur approchée de \( P(X \le x) \) , on doit utiliser une table de loi. Nous allons donc voir théoriquement, puis à l’aide d’exemples concrets, comment lire ce tableau de valeurs pour trouver ce que l’on recherche en fonction de la valeur de \(x\).
Interprétation globale de la table de loi

Voici comment se présente une table de loi \(\mathcal{N}(0,1) \). On lit dans la table de loi ci-dessus les différentes valeurs que peut prendre \(P(X \le x)\) lorsque \(x\) est positif.
Les différentes colonnes vont nous permettre de trouver le chiffre des centièmes de la valeur de \(x\) que l’on recherche, en s’incrémentant d’un centième par colonne. Les différentes lignes vont nous permettre de trouver les chiffres des dixièmes et des unités pour la valeur de \(x\) que l’on recherche, en s’incrémentant d’un dixième par ligne.
Cas 1
Je recherche \( P(X \le x)\) avec \( X \hookrightarrow \mathcal{N}(0,1) \).
Dans ce premier cas, il suffit de lire la table de loi comme présenté dans le cas général.
Prenons un exemple concret :
Je cherche \( P(X \le 3,14)\)
On commence par décomposer \(3,14\) entre unités et dixièmes d’un côté et centièmes de l’autre : \( \color{red}{3}, \color{red}{1} \color{DeepSkyBlue}{4} \)
On se réfère ensuite à la table de loi en regardant les unités et les dixièmes dans les lignes et les centièmes dans les colonnes.

Au final, on voit donc que \( P(X \le 3,14) = 0,9992 \).
Cas 2
Je recherche \( P(X > x)\) avec \( X \hookrightarrow \mathcal{N}(0,1) \).
Dans cette situation, il est judicieux de passer au complémentaire.
Par ailleurs, il est bon de rappeler que comme la loi normale centrée réduite est à densité, la valeur de sa fonction de répartition en un point est nulle et ainsi on a \( P(X > x) = P(X\ge x) \).
Prenons un exemple concret :
Je cherche \( P(X > 2,67) \)
On commence par décomposer \(2,67\) entre les dixièmes et les centièmes :
\( \color{red}{2}, \color{red}{6} \color{DeepSkyBlue}{7} \)
Puis, on se réfère à la table de loi comme dans le cas précédent.
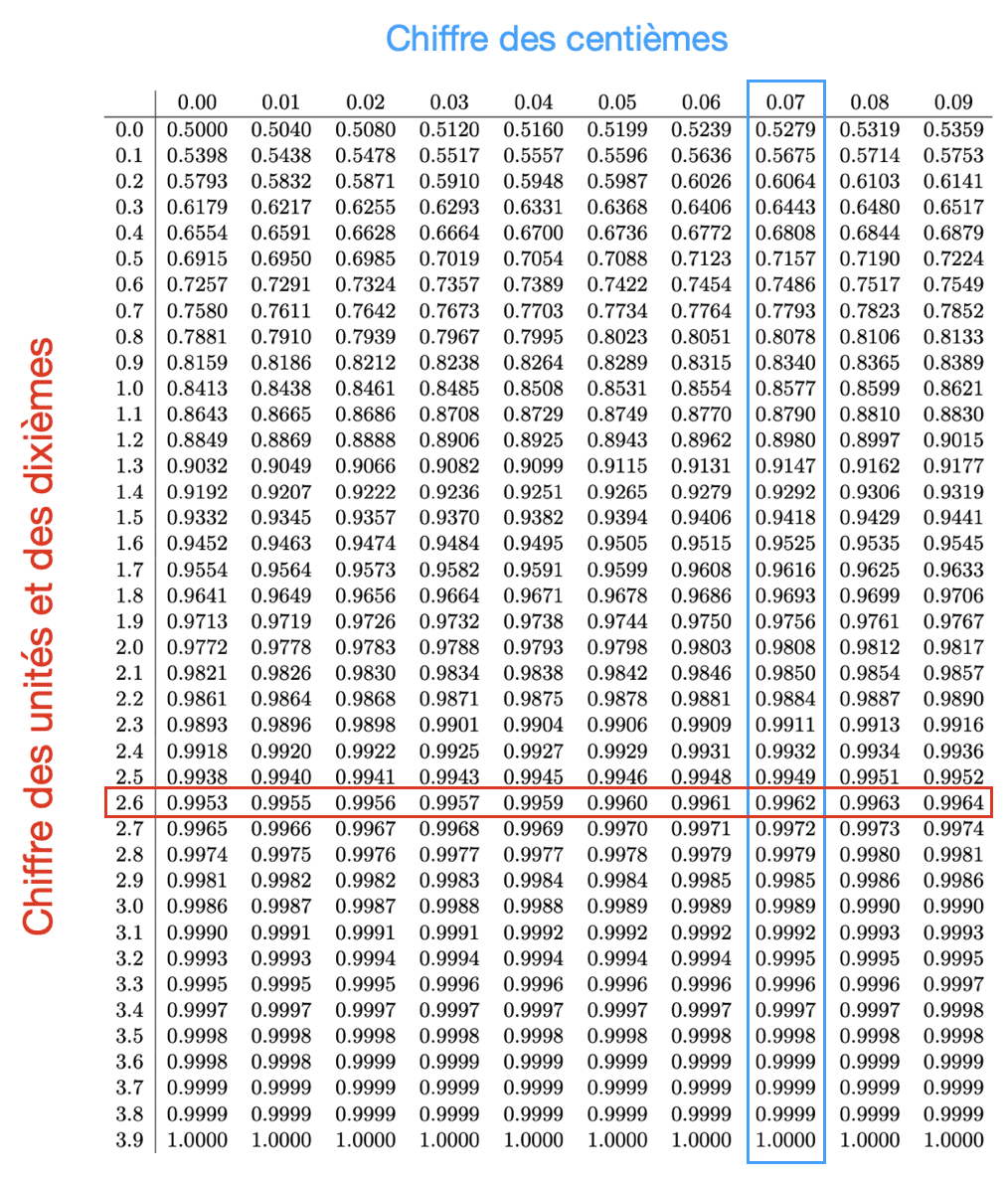
On passe ensuite au complémentaire :
\(\begin{align}
P(X>2,67) &= 1 \text{ }- P(X \le 2,67)\\
&= 1-0,9962 \\
&= 0,0038
\end{align} \)
Au final, on voit donc que \( P(X>2,67)= 0,0038\).
Cas 3
Je cherche \(P(x_{1} \le X \le x_{2})\) avec \( X \hookrightarrow \mathcal{N}(0,1) \).
Dans ce cas-là, on utilise les propriétés d’une fonction de répartition, soit \(P(x_{1} \le X \le x_{2}) = P(x_{2} \le X) \text{ }- P(x_{1} \le X)\).
Prenons un exemple concret :
Je cherche \( P( 2,67 \le X \le 3,14) \).
La recherche des valeurs de \( P(X \le 2,67)\) et de \( P(X \le 3,14)\) se fait comme dans le premier cas.
\( \begin{align}
P( 2,67 \le X \le 3,14) &= P(X \le 3,14) \text{ }- P(X \le 2,67)\\
&= 0,9992 – 0,9962 \\
&= 0,0030
\end{align} \)
Au final, on voit donc que \( P(2,67 \le X \le 3,14)= 0,0030\).
Cas 4
On me donne une valeur et je dois en trouver la probabilité.
Le tableau permet de nous donner une valeur approchée d’une probabilité, mais on peut aussi nous donner une valeur approchée d’une probabilité utilisant la loi normale centrée réduite et nous demander quelle probabilité a été calculée.
Il suffit alors de procéder comme pour le premier exercice, mais en commençant par la fin.
Prenons un exemple concret :
On me donne \(0,7673\) comme valeur et on me demande quelle probabilité correspond à cette valeur.

Je commence par trouver cette valeur dans le tableau (plus on va en bas à droite du tableau, plus les valeurs sont grandes, ce qui est logique car on a alors un \(x\) que l’on cherche plus grand).
Une fois que j’ai trouvé cette valeur, je me reporte à gauche de la ligne pour trouver les chiffres des unités et des dixièmes, puis en haut de la colonne pour trouver celui des centièmes.
Ici, on remarque que c’est \( P(X \le 0,73) \) qui donne \(0,7673\).
Remarque : On voit que certaines valeurs sont présentes plusieurs fois dans le tableau, on ne te donnera pas celles-là ou alors on te donnera un (ou plusieurs) indice(s) (chiffre des centièmes égal à 9, par exemple).
Cas 5
J’ai un tableau de valeurs positives et je cherche une probabilité négative.
Il est possible que l’on te donne à trouver \( P(X \le x)\) avec \(x \le 0\), alors que ta table de loi est construite pour des valeurs positives. Il ne faut pas paniquer et se servir de toutes les propriétés de la loi normale centrée réduite (un peu de maths quand même !).
Avoir en tête cette propriété : \(\forall x \in \mathbb R, \Phi(x)=1-\Phi(-x)\)
Petit rappel de sa démonstration :
Soit \( X \hookrightarrow \mathcal{N}(0,1) \). On sait que :
\(\begin{align}
\forall x \in \mathbb R, \Phi(x)&= P(X \le x) \\
&=\frac{1}{\sqrt{2\pi}}\displaystyle \int_{-\infty}^{x} e^{\frac{-t^2}{2}} \mathrm{d}t\\
&= \frac{1}{ \sqrt{2\pi}}\displaystyle \int_{-x}^{+\infty} e^{\frac{-u^2}{2}} \mathrm{d}u \text{ (changement de variable affine } t=-u)\\
&=1 – {\sqrt{2\pi}}\displaystyle \int_{-\infty}^{-x} e^{\frac{-u^2}{2}} \mathrm{d}u \\
&= 1- P(X \le -x) \\
&=1-\Phi(-x)
\end{align}\)
Prenons un exemple concret :
J’ai le tableau précédent et on me demande \( P(X \le -1,34)\)
D’après la propriété ou la démonstration précédente, \( P(X \le -1,34) = 1 – \Phi(1,34) = 1 – P(X\le 1,34)\).

On utilise toujours la même technique pour repérer que \( P(X \le \color{red}{1}, \color{red}{3} \color{DeepSkyBlue}{4})=0,9099 \)
\(\begin{align}
\text{Au final, on voit donc que : } P(X \le -1,34) &=1 – P(X \le 1,34) \\
&=1 -0,9099 \\
&=0,0901
\end{align}\)
Cas 6
La valeur de \(x\) que je cherche est trop précise pour la table de loi.
La table de loi donne généralement une valeur approchée au centième près, et il se peut que le sujet nous demande une valeur plus précise que cela.
Deux solutions s’offrent à nous et elles peuvent nous être imposées, ou on peut prendre nous-mêmes une initiative. Soit on arrondit au supérieur (ou à l’inférieur), soit on procède à un encadrement.
Pour ce qui est d’arrondir au supérieur ou à l’inférieur, il ne s’agit ni plus ni moins que d’enlever le chiffre des millièmes et d’utiliser la méthode du premier cas.
Pour ce qui est de réaliser un encadrement, voici la méthode
Prenons un exemple concret :
Je dois trouver \(P(X \le 2,892)\)
Je peux encadrer de cette façon au centième près : \(2,89 \le 2,892 \le 2,90\).
Il ne me reste alors plus qu’à calculer \(P(X \le 2,89)\) et \(P(X \le 2,90) \) en procédant comme dans le premier cas.

On trouve \(P(X \le 2,89)=0,9981\) et \( P(X \le 2,90)=0,9981\)
On ne peut alors pas encadrer \(P(X \le 2,892)\), mais on sait que \(0,9981\) est une bonne valeur approchée pour cette probabilité.
N’hésite pas à consulter toutes nos ressources de mathématiques.