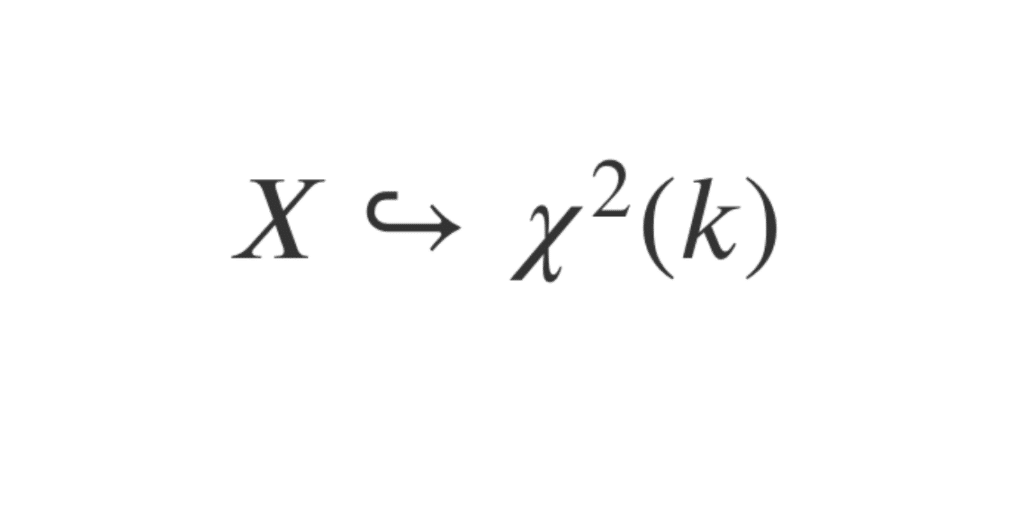
Aujourd’hui, nous allons nous intéresser à un classique des annales parisiennes : la loi du khi deux. Dans le domaine de la statistique, la prise de décision repose sur la capacité à tirer des conclusions à partir de données empiriques. Pour cela, il existe un grand nombre de tests et de méthodes, mais l’une des méthodes les plus puissantes est la loi du khi deux. Dans cet article, je te présente l’utilité de cette loi et plusieurs de ses propriétés, qui te seront utiles lors de ta préparation aux Maths I et II.
La loi du khi deux, expliquée en français
La loi du khi deux de paramètre \( k \in \mathbb{N}^* \) est la loi de la somme de carrés de \(k\) lois normales centrées réduites mutuellement indépendantes.
En statistiques, cette loi trouve de nombreuses applications, notamment pour les tests du \( \chi^2 \) qui permettent de calculer l’écart entre la distribution observée dans un échantillon avec une distribution théorique (test d’ajustement), de tester si les échantillons observés proviennent d’une même population (test d’homogénéité) et de tester si deux paramètres d’une population sont indépendants (test d’indépendance).
Définition de la loi du khi deux
Définition à l’aide de la loi normale
Soient \(k\) variables aléatoires mutuellement indépendantes, \(X_1, …, X_k, \) qui suivent une loi normale centrée réduite.
Posons \(X=\displaystyle \sum_{i=1}^k X_i^2, \) alors \( X \hookrightarrow \chi^2(k) \)
Définition à l’aide de la loi gamma
\( \forall k \in \mathbb{N}^*, X \) suit la loi du khi deux de paramètre k si la variable aléatoire \( \displaystyle \frac{X}{2} \) suit la loi gamma de paramètre \( \displaystyle \frac{k}{2}\).
Fonction de répartition et densité
\( X \hookrightarrow \chi^2(k) \)
Pour déterminer la fonction de répartition et la densité de \( X \), nous pouvons utiliser l’indication ci-dessus qui nous précise que \( \displaystyle\frac{X}{2} \) suit la loi gamma de paramètre \( \displaystyle \frac{k}{2}\).
Ainsi : \( \fbox{\(x \mapsto \begin{cases} \displaystyle\frac{x^{\frac{k}2-1}e^{-\frac{x}{2}}}{\Gamma(\frac{k}2)2^\frac{k}2} \; \; \; \text{si} \;x > 0\\
0 \; \; \; \text{sinon} \end{cases} \text{} \)} \) est une densité de \( X \).
De plus : \( \fbox{\(x \mapsto \begin{cases} \displaystyle\frac{\displaystyle\int_0^{\frac{x}2}t^{\frac{k}2-1}e^{-t}\mathrm{d}t}{\Gamma(\frac{k}2)} \; \; \; \text{si} \;x > 0\\
0 \; \; \; \text{sinon} \end{cases} \text{} \)} \) est la fonction de répartition de \( X \).
Espérance et variance
\( X \hookrightarrow \chi^2(k) \)
Pour le calcul de l’espérance et de la variance, il n’est pas nécessaire d’utiliser la densité, car la définition de la loi du khi deux suffit. En effet, \(X=\displaystyle \sum_{i=1}^k X_i^2 \) tel que \( \forall i \in [\![1,k]\!], X_i \hookrightarrow \mathcal{N}(0,1)\) avec l’indépendance mutuelle des \( (X_i)\).
\(
\begin{align}
\text{Donc :} \; \mathbb{E}(X)&=\mathbb{E}(\displaystyle \sum_{i=1}^k X_i^2 ) \\
&=\displaystyle \sum_{i=1}^k \mathbb{E}(X_i^2) \\
&=\displaystyle \sum_{i=1}^k \left ( V(X_i^2) +\mathbb{E}(X_i)^2 \right ) \\
&=\displaystyle \sum_{i=1}^k (1+0)\\
&=k
\end{align}
\)
\(
\begin{align}
\text{De même :} \; V(X)&= V\left ( \displaystyle \sum_{i=1}^k X_i^2 \right ) \\
&= \displaystyle \sum_{i=1}^k V(X_i^2)\; \;\text{(car les \( X_i^2\) sont mutuellement indépendantes)}\\
&=\displaystyle \sum_{i=1}^k \left (\mathbb{E}(X_i^4)-\mathbb{E}(X_i^2)^2 \right ) \ \\
&=\displaystyle \sum_{i=1}^k (3-1) \; \; \text{(le moment d’ordre 4 se trouve par IPP)}\\
&=2k
\end{align}
\)
D’où : \( \fbox{\( \mathbb{E}(X)=k \)} \; \;\text{et} \; \; \fbox{\( V(X)=2k \)} \)
Conclusion
En résumé, la loi du khi deux est une loi avec des applications diverses et des propriétés en lien avec de nombreuses lois au programme. Ainsi, bien que cette loi soit hors programme, sa compréhension approfondie enrichira ta préparation aux épreuves parisiennes, notamment aux Maths II !
Tu peux d’ailleurs t’entraîner sur des sujets (mathématiques approfondies) de concours abordant la loi du khi deux :
Tu peux retrouver ici toutes nos autres ressources mathématiques !
