L’algorithme de Dijkstra

L’algorithme de Dijkstra est une brique fondatrice du programme de CPGE en informatique, notamment en mathématiques appliquées. En effet, ce petit programme est le plus complexe qu’un élève aura à réaliser au cours de sa scolarité et représente le plus haut niveau de maîtrise du code Python, que ce soit en première année ou bien en deuxième année.

Cet article s’adresse aux étudiants aussi bien en première année qu’en deuxième année, étant donné que le programme de Dijkstra est abordé en première année, mais reste essentiel pour la deuxième année.

Pour ceux en première année, il ne faut pas paniquer si le programme semble complexe, étant donné que l’objectif sera de le comprendre en fin d’année. Cependant, si le programme n’est toujours pas compris en deuxième année, il faut impérativement reprendre les cours de première année bien avant de pousser Python plus loin.

Cet article s’adresse à ceux déjà à l’aise en Python.

Motivation du programme de l‘Algorithme de Dijkstra

Théorie des graphes

Comprendre la théorie des graphes est absolument essentiel pour saisir ce qu’on pourrait appeler le « concept de Dijkstra ». Cependant, que ce soit pour clarifier les choses, prendre de l’avance ou simplement réviser, voici un petit point de cours.

• Un graphe est défini par deux choses :
  • Une liste d’arêtes, généralement notée « A » en cursive
  • Une liste de sommets, généralement notée « S » en cursive
• Il faut se souvenir qu’un graphe ne veut pas dire une représentation graphique, loin de là
• Les arêtes d’un graphe peuvent avoir un « poids », indiqué sur le graphe comme sur la matrice d’adjacence, comme suit :

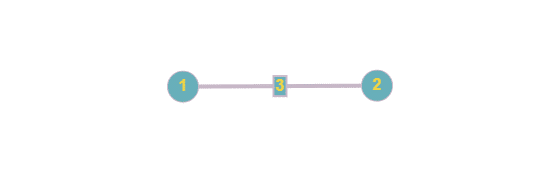
• Les arêtes du graphe peuvent être orientées, c’est-à-dire pointer d’un sommet vers un autre, comme suit (sinon on compte une arête non orientée comme allant dans les deux sens) :

• En informatique, le graphe est représenté par une matrice d’adjacence, qui comporte, au i-ème coefficient de la j-ème ligne, un « 1 » s’il y a une arête allant du sommet « i » au sommet « j », et un 0 sinon. Ci-dessous, on pourra trouver la matrice d’adjacence A du graphe ci-dessus

\[A=\begin{bmatrix}0&1\\0&0\end{bmatrix}\]

Spécificités de Dijkstra

Le concept relève d’un état d’esprit particulier concernant la recherche d’un plus court chemin dans le graphe, soit la recherche du plus court chemin de façon naïve en observant les chemins empruntés si l’on rejoint les sommets voisins. Il existe des programmes bien plus efficaces que celui-ci.

Ce programme ne renverra pas le chemin le plus court, mais une liste de type list, où chaque élément de la liste d’indice « i » est la longueur du chemin qui commence du sommet sélectionné pour le départ jusqu’au sommet « i ».

Prérequis

Pour réaliser ce programme, il faut au préalable avoir une bonne compréhension de la représentation des graphes en Python, avec notamment les matrices d’adjacence.

De plus, afin de modéliser les distances inconnues, on utiliser np.inf, soit l’attribut inf de la librairie numpy. Il ne faut ainsi pas avoir une maîtrise poussée de numpy, mais seulement raisonnable pour comprendre cette dernière commande.

Fonctionnement de l’algorithme de Dijkstra

Variables mises en jeu

• Arguments
  • « aretes » : la liste des arêtes présente dans le graphe
  • « sommets » : la liste des sommets, soit une liste de nombres, commençant à 0, pour rendre le programme plus lisible
  • « sommet_depart » : le sommet de départ, modélisé par un numéro

• Autres variables
  • « distances » : la liste des distances entre « sommet_depart » et les sommets du graphe, placés dans la liste à l’indice de leur numéro de sommet
  • « sommets_visites » : liste des sommets visités, avec les numéros de ces sommets

On peut ainsi voir qu’il n’y a que très peu de variables mises en jeu dans le programme. Sa complexité réside en fait dans deux petits algorithmes qu’il faudra implémenter à l’intérieur de l’algorithme global.

Fonctionnement

• On initialise les distances (« distances ») de tous les sommets à l’infini : on n’a aucune information les concernant
• On met le sommet de départ (« sommet_depart ») à une distance 0 puisque l’on part de ce sommet
• On n’a visité aucun sommet, donc on crée une liste de sommets visités (« sommets_visites ») qui est vide
•  Tant qu’il y a des distances infinies dans les sommets non visités (pour être sûr de ne pas manquer le chemin le plus court) :
  • On détermine le sommet le plus proche, non visité, du sommet où on est et on y voyage
  • On détermine les voisins du sommet où on arrive
    • Comparaison de la distance déjà calculée des voisins avec la distance obtenue si on passe par le sommet où l’on est
    • Si la distance, en passant par le sommet où l’on est, est plus petite que la distance en mémoire, on la met à jour pour obtenir la plus petite distance possible
  • On marque le sommet comme visité
• On retourne la liste des distances (« distances »)

On pourra faire un schéma pour s’aider, en utilisant un graphe quelconque.

Programme

Programme complet et commentaires

Trouver le sommet voisin le plus proche, non visité, d’un sommet (L6-L10)

Trouver le sommet le plus proche revient à trouver la valeur minimale de la liste de distances.

• On construit une variable « distance_minimale », la plus grande possible, donc avec inf, pour la réduire au fur et à mesure et ainsi trouver la distance minimale
• On parcourt la liste des distances aux autres sommets
  • Si le sommet n’est pas visité et que la distance à ce sommet est plus petite que la distance minimale, strictement
    • « distance_minimale » prend la valeur de la distance à ce sommet
    • On retient ce sommet

Déterminer les sommets voisins d’un sommet

• On définit une liste « voisins » en regardant les coefficients non nuls de la matrice d’adjacence
• On parcourt cette liste
  • Si la distance (« sommet_depart » – sommet voisin) est plus grande que la (distance du « sommet_depart » – sommet actuel) plus la distance (sommet actuel – sommet voisin), on met à jour la distance

Bilan

Pour comprendre ce programme déjà complexe, il ne faut surtout pas hésiter à faire un schéma quand cela est nécessaire pour se clarifier les idées. Dijkstra n’est que la première pièce du puzzle de cette catégorie d’algorithmes qui trouvent les chemins les plus courts pour nous permettre, dans la vie, d’utiliser un GPS (comme Waze, par exemple).

N’hésite pas à consulter toutes nos ressources en mathématiques !