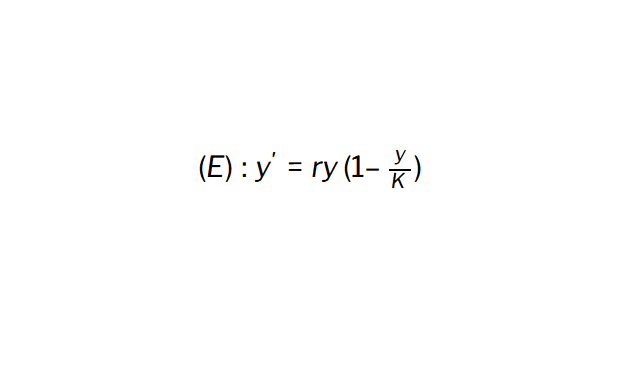L’équation différentielle logistique est un classique (bien qu’un peu complexe) du hors-programme ECG en maths appliquées. Il est à peu près certain que la résolution de cette équation différentielle tombera un jour au concours, probablement lors d’une épreuve parisienne. De fait, elle est en particulier liée au modèle de populations de Verhulst, que les professeurs de mathématiques affectionnent particulièrement.
Je vais donc ici te présenter cette équation différentielle, te montrer les différentes étapes de sa résolution. Pour finir, je t’expliquerai le lien entre cette équation différentielle et le modèle de Verhulst.
Présentation de l’équation différentielle logistique
L’équation différentielle dite « logistique » est une équation différentielle non linéaire : c’est là que réside toute la difficulté.
Elle se présente ainsi :
Soit \( (r, K) \in \mathbb{R}_{+}^{*} \times \mathbb{R}_{+}^{*} \).
On a alors l’équation différentielle logistique de paramètres \((r, K)\) définie par \((E) : y’ = ry\left(1 – \frac{y}{K}\right)\), d’inconnue \(y \in \mathcal{A}(\mathbb{R}_{+}, \mathbb{R}_{+}^{*})\). C’est-à-dire que l’inconnue est une fonction \(y\) partant de l’intervalle \(\mathbb{R}_{+}\) et arrivant dans l’intervalle \(\mathbb{R}_{+}^{*}\).
Cette équation modélise l’évolution d’une population en milieu fermé. Elle a été formulée pour la première fois en 1840 par Pierre-François Verhulst.
Le terme \(ry\) (obtenu en développant à droite) modélise le fait qu’il existe un accroissement naturel de la population (puisque \(r \in \mathbb{R}_{+}^{*} \)), tandis que le terme \( -rKy^{2} \) (que l’on obtient en développant encore une fois) donne une limite à cet accroissement (puisque \(r\) et \(K\) sont dans \(\mathbb{R}_{+}^{*}\)).
Voyons maintenant comment résoudre une telle équation malgré le fait qu’elle ne soit pas linéaire.
Résolution de l’équation différentielle logistique
Pour résoudre cette équation différentielle, il faut avoir une idée. C’est pour cette raison que sa résolution sera (peut-être) guidée dans un sujet de concours.
Néanmoins, il est important que tu connaisses l’astuce afin de ne pas perdre de temps pour le cas où la résolution serait guidée. Et surtout pour ne pas être bloqué(e) si elle venait à ne pas l’être.
Étape 1
L’astuce est la suivante : on va montrer que \(y\) est solution de \((E)\) si et seulement si \(\frac{1}{y}\) est solution d’une autre équation différentielle \((F)\) que l’on va déterminer.
On a alors l’équivalence suivante :
\(
\begin{align}
y \text{ est solution de } E &\Leftrightarrow \forall t \in \mathbb{R}, \ y'(t) = ry(t) \left(1 – \frac{y(t)}{K}\right) \\
&\Leftrightarrow \forall t \in \mathbb{R}, \ y'(t) = ry(t) – \frac{ry^2(t)}{K} \\
&\Leftrightarrow \forall t \in \mathbb{R}, \ -y'(t) = -ry(t) + \frac{ry^2(t)}{K} \\
&\Leftrightarrow \forall t \in \mathbb{R}, \ \frac{-y'(t)}{y^{2}(t)} = \frac{-r}{y(t)} + \frac{r}{K} \\
&\Leftrightarrow \forall t \in \mathbb{R}, \ (\frac{1}{y(t)})’ + r\frac{1}{y(t)} = \frac{r}{K} \\
&\Leftrightarrow \frac{1}{y} \text{ est solution de } (F) : x’ + rx = \frac{r}{K} \text{ et } \forall t \in \mathbb{R}^+, \ y(t) > 0 \ (\text{puisque} \ y \in \mathcal{A}(\mathbb{R}_{+}, \mathbb{R}_{+}^{*}))
\end{align}
\)
Étape 2
Il nous suffit maintenant de résoudre l’équation différentielle \( (F) : x’ +rx = \frac{r}{K} \). Ce que l’on peut faire relativement aisément avec les techniques classiques de résolution.
Tout d’abord, les solutions homogènes sont de la forme \( f : \begin{cases} R \to R \\x \mapsto C \times e^{-rt}, \ C \in \mathbb{R} \end{cases} \)
De plus, selon la formule classique permettant de trouver une solution particulière dans le cas d’un second membre qui est une fonction constante, on trouve qu’une solution particulière est la fonction \( g : \begin{cases} R \to R \\x \mapsto \frac{1}{K} + C \times e^{-rt}, \ C \in \mathbb{R} \end{cases} \)
Étape 3
Il est maintenant temps de résoudre (E).
Soit \( y \in \mathcal{A}(\mathbb{R}_{+}, \ \mathbb{R}_{+}^{*}) \) (c’est-à-dire que l’on prend une fonction \(y\) dans l’ensemble des fonctions ayant pour ensemble de départ \( \mathbb{R}_{+} \) et pour ensemble d’arrivée \( \mathbb{R}_{+}^{*}) \)
Alors, on a l’équivalence suivante :
\(
\begin{align}
y \text{ est solution de } (E) &\Leftrightarrow \frac{1}{y} \text{ est solution de } (F) : x’ + rx = \frac{r}{K} \text{ et } \forall t \in \mathbb{R}_{+}, y(t) > 0 \\
&\Leftrightarrow \exists C \in \mathbb{R}, \forall t \in \mathbb{R}_{+}, \frac{1}{y(t)} = Ce^{-rt} + \frac{1}{K}, \text{ et } \forall t \in \mathbb{R}_{+}, y(t) > 0 \\
&\Leftrightarrow \begin{cases}
\exists C \in \mathbb{R}, \forall t \in \mathbb{R}_{+}, \frac{1}{y(t)} = Ce^{-rt} + \frac{1}{K} \\
\frac{1}{y(0)} = Ce^{0} + \frac{1}{K} \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
&\Leftrightarrow \begin{cases}
\exists C \in \mathbb{R}, \forall t \in \mathbb{R}_{+}, \frac{1}{y(t)} = Ce^{-rt} + \frac{1}{K} \\
C = \frac{1}{y(0)} – \frac{1}{K} \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
&\Leftrightarrow \begin{cases}
\forall t \in \mathbb{R}_{+}, \frac{1}{y(t)} = (\frac{1}{y(0)} – \frac{1}{K}) \times e^{-rt} + \frac{1}{K} \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
&\Leftrightarrow \begin{cases}
\forall t \in \mathbb{R}_{+}, \frac{1}{y(t)} = \frac{1}{K} \times \left(\left(\frac{K}{y(0)} – 1\right) \times e^{-rt} + 1\right) \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
&\Leftrightarrow \begin{cases}
\forall t \in \mathbb{R}_{+}, y(t) = \frac{1}{\frac{1}{K} \times \left(\left(\frac{K}{y(0)} – 1\right) \times e^{-rt} + 1\right)} \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
&\Leftrightarrow \begin{cases}
\forall t \in \mathbb{R}_{+}, y(t) = \frac{K}{\left(\left(\frac{K}{y(0)} – 1\right) \times e^{-rt} + 1\right)} \\
\forall t \in \mathbb{R}_{+}, y(t) > 0 \\
\end{cases} \\
\end{align}
\)
Puisque l’on sait que \(r\) et \(K\) sont dans \( \mathbb{R}_{+}^{*} \times \mathbb{R}_{+}^{*} \), on peut montrer que : \( \forall t \in \mathbb{R}_{+}, y(t) > 0 \), ce qui nous permet d’enlever la dernière condition.
Démontrons-le
Premièrement,
Si l’expression \( \frac{K}{y(0)} – 1 \) est supérieure ou égale à 0, on a :
\(
\begin{align}
\frac{K}{y(0)} – 1 \ge 0 &\Rightarrow K \ge y(0)
\end{align}
\)
Dès lors, notre expression de \(y\) est bien positive pour tout \( t \in \mathbb{R}_{+} \), puisque exponentielle est une fonction positive sur \( \mathbb{R} \).
Deuxièmement,
Si l’expression \( \frac{K}{y(0)} – 1 \) est strictement inférieure à 0, on a :
\(
\begin{align}
\frac{K}{y(0)} – 1 < 0 &\Rightarrow K < y(0)
\end{align}
\)
Posons : \( \forall t \in \mathbb{R}_{+}, g(t) = \frac{K}{\left(\left(\frac{K}{y(0)} – 1\right) \times e^{-rt} + 1\right)} \)
Ensuite, il suffit d’étudier la fonction \(g\). Ce faisant, en dérivant, on obtient la stricte croissance de \(g\) sur \( \mathbb{R}_{+} \) par stricte positivité de la dérivée de \(g\) sur ce même intervalle. Je te laisse calculer la dérivée de \(g\), qui n’est pas compliquée à trouver.
Ceci nous donne que : \( \forall t \in \mathbb{R}_{+}, g(t) \ge g(0) \).
Or, \( g(0) = \frac{1}{y(0)} \)
Or, \( y(0) \in \mathcal{A}(\mathbb{R}_{+}, \ \mathbb{R}_{+}^{*}) \), c’est-à-dire que \(y\) est une fonction de \( \mathbb{R}_{+} \ \text{dans} \ \mathbb{R}_{+}^{*} \).
Donc, forcément, \( y(0) \in \mathbb{R}_{+}^{*} \)
Donc : \( \forall t \in \mathbb{R}_{+}, g(t) > 0 \)
Donc, dans tous les cas, notre fonction \(y\) est bien strictement positive. On peut enlever la dernière contrainte et se contenter de dire que l’ensemble solution de notre équation différentielle logistique est \( S_{E} : \begin{cases} \mathbb{R}_{+} \to \mathbb{R}_{+}^{*} \\t \mapsto \frac{K}{\left(\left(\frac{K}{y(0)} – 1\right) \times e^{-rt} + 1\right)}, \ C \in \mathbb{R} \end{cases} \)
Le lien avec le modèle d’évolution de population
Pour voir le lien entre cette équation différentielle et un modèle complexe d’évolution d’une population, il convient de s’intéresser au comportement asymptotique de la fonction \(y\), qui fait ici office de solution.
De fait, on a très simplement (par les opérations usuelles sur les limites) que \( \lim \limits_{t \to +\infty} y(t) = K \)
Or, on peut montrer que la fonction constante \( f : \begin{cases} \mathbb{R}_{+} \to \mathbb{R} \\t \mapsto K \end{cases} \) est bien solution de \((E)\).
De fait,
\(
\begin{align}
f \text{ est solution de } E &\Leftrightarrow \forall t \in \mathbb{R}_{+}, \ f'(t) = rf(t) \left(1 – \frac{f(t)}{K}\right) \\
&\Leftrightarrow \forall t \in \mathbb{R}_{+}, 0 = rK \left(1 – \frac{K}{K}\right) \\
&\Leftrightarrow \forall t \in \mathbb{R}_{+}, 0 = rK \times 0 \\
&\Leftrightarrow \forall t \in \mathbb{R}_{+}, 0 = 0
\end{align}
\)
Donc, \(K\) est bien un équilibre de \( (E) \).
Donc, par définition, toutes les solutions de \( (E) \) convergent vers un équilibre de \( (E) \) qui est \( f : \begin{cases} \mathbb{R}_{+} \to \mathbb{R} \\t \mapsto K \end{cases} \).
C’est pour cette raison que dans ce modèle, \(r\) est appelé le « taux de croissance », tandis que \(K\) est appelé la « capacité d’accueil ». Le modèle prévoit que la population finira forcément par converger vers \(K\), qui n’est rien d’autre que la capacité d’accueil asymptotique du milieu dans lequel évolue la population.
Conclusion
Voilà, tu sais maintenant tout ce qu’il y a à savoir sur l’équation différentielle logistique. Je peux te garantir que la résolution de cette équation différentielle tombera dans les prochaines années pour les maths appliquées. Je t’encourage donc à bien comprendre le cheminement de sa résolution pour être à l’aise si tu dois à un moment résoudre toi-même cette équation.
Sinon, tu peux retrouver toutes nos autres ressources mathématiques ici.