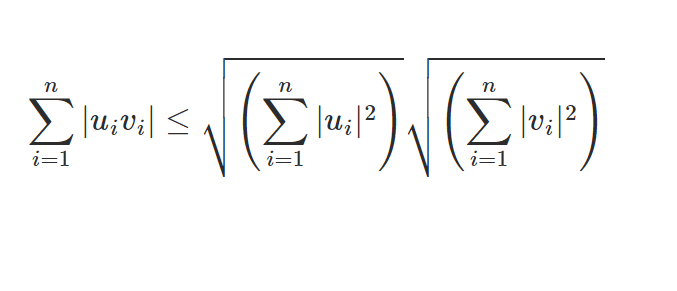Les notions hors programme sont à travailler en priorité par les candidats visant les trois Parisiennes. Cet article te propose de découvrir deux démonstrations de l’inégalité de Cauchy-Schwarz ainsi qu’une application intéressante. L’inégalité de Cauchy-Schwarz et les techniques qu’elle invoque sont assez récurrentes dans les sujets de concours. Cet article est là pour mieux t’aider à la comprendre et y être sensibilisé(e) afin de ne pas être pris(e) au dépourvu le jour J. Cela te simplifiera également la tâche pour ficher.
Énoncé du théorème
Soit E un espace vectoriel muni d’un produit scalaire \( \langle\cdot,\cdot\rangle \).
Pour tout couple \( (x,y) \) de vecteurs de \( E \), on a :
\[ \displaystyle \big| \langle x,y \rangle \big| \le \big\| x \big| \big\| y \big\| \hspace{2pt} \text{ ou } \hspace{2pt} \langle x,y \rangle^2 \le \big\| x \big\|^2\big\| y \big\|^2 \]
Avec égalité si, et seulement si, la famille (x,y) est liée.
Démonstrations de l’inégalité de Cauchy-Schwarz
Première méthode
Cette méthode repose sur l’utilisation d’un polynôme particulier.
Soit \( x \) et soit \( y \) deux vecteurs de \( E \).
- Si \( x=0 \), la famille \( (x,y) \) est liée et on a :
\[ \langle x,y \rangle = 0 \hspace{2pt} \text{ et } \hspace{2pt} \big\| x \big\| \big\| y \big\| = 0 \]
Donc, l’inégalité et l’égalité sont vraies.
On suppose dans la suite que \( x \) et \( y \) sont non nuls
- On peut remarquer que :
\[ \forall \lambda \in \mathbb{R}, \big\| \lambda x+y \big\|^2 = \big\| x \big\|^2 \lambda^2 + 2\langle x,y\rangle \lambda + \big\| y \big\|^2 \]
Donc, \( P : \lambda \mapsto \big\| \lambda x+y \big\|^2 \) est une fonction polynôme, de degré 2 et à coefficients réels. De plus, par définition de \( P \) et par positivité de la norme, on a :
\[ \forall \lambda \in \mathbb{R}, P(\lambda) \ge 0 \]
Comme \( P \) est un polynôme de degré 2 à coefficients réels, on en déduit que \( P \) admet au plus une racine réelle, donc que son discriminant est négatif ou nul, c’est-à-dire :
\[ 4\langle x,y\rangle^2 – 4\big\| x\big\|^2 \big\| y\big\|^2 \le 0 \]
Et donc :
\[ \langle x,y\rangle^2 \le \big\| x\big\|^2 \big\| y\big\|^2 \]
et comme la fonction \( t \mapsto \sqrt{t} \) est croissante sur \( \mathbb{R}^+ \) :
\[ \big| \langle x,y\rangle \big| \le \big\| x\big\| \cdot \big\| y\big\| \]
- Supposons maintenant que :
\[ \big| \langle x,y\rangle \big| = \big\| x\big\| \cdot \big\| y\big\| \]
On a alors :
\[ 4\langle x,y\rangle^2 – 4\big\| x\big\|^2 \big\| y\big\|^2 = 0 \]
Ce qui prouve que P admet une racine réelle \( \alpha \) , et alors :
\[ \big\| \alpha x + y \big\| = 0 \]
Et donc :
\[ \alpha x + y = 0 \]
Ce qui prouve que la famille \( (x,y) \) est liée.
- Supposons enfin que la famille \( (x,y) \) soit liée. Comme \( x \ne 0 \), il existe alors \( \alpha \in \mathbb{R} \) tel que : \( y=\alpha x \) et alors :
\[ \big| \langle x,y \rangle \big| = \big| \alpha \big| \big| \langle x,x \rangle \big| \hspace{2pt} \text{ et } \hspace{2pt} \big\| x \big\| \big\| y \big\| = \big| \alpha \big| \big\| x \big\|^2 \]
Et donc :
\[ \big| \langle x,y \rangle \big| = \big\| x \big\|\big\| y \big\| \]
Deuxième méthode
Soit \( (u,v) \in E^2 \).
Si \( u=0_{E} \) ou \( v=0_{E} \), alors l’inégalité est évidente.
Supposons \( u \) et \( v \) non nuls.
On a :
\begin{align} \bigg\| \frac{u}{\big\| u \big\|} \pm \frac{v}{\big\| v \big\|} \bigg\|^2 & = \bigg\| \frac{u}{\big\| u \big\|} \bigg\|^2 \pm 2\frac{\langle u,v\rangle}{\big\| u \big\| \cdot \big\| v \big\|} + \bigg\| \frac{v}{\big\| v \big\|} \bigg\|^2 \\ & = 1 \pm 2\frac{\langle u,v\rangle}{\big\| u \big\| \cdot \big\| v \big\|}\\ & = 2\left(1 \pm \frac{\langle u,v\rangle}{\big\| u \big\| \cdot \big\| v \big\|}\right). \end{align}
Comme :
\[ \bigg\| \frac{u}{\big\| u \big\|} \pm \frac{v}{\big\| v \big\|} \bigg\|^2 = 0 \]
On en déduit que :
\[ 1 \pm \frac{\langle u,v\rangle}{\big\| u \big\| \cdot \big\| v \big\|} \ge 0 \]
Soit :
\[ -1 \le \frac{\langle u,v\rangle}{\big\| u \big\| \cdot \big\| v \big\|} \le 1 \]
Ou encore :
\[ \big| \langle u,v \rangle \big| \le \big\| u \big\|\big\|v \big\|. \]
On a égalité si, et seulement si, on a :
\[ \bigg\| \frac{u}{\big\| u \big\|} \pm \frac{v}{\big\| v \big\|} \bigg\|^2 =0 \]
C’est-à-dire, si et seulement si :
\[ \frac{u}{\big\| u \big\|} = \pm \frac{v}{\big\| v \big\|} \]
Autrement dit, si, et seulement si, \( u \) et \( v \) sont liés.
Utilisation classique et intéressante de la méthode de démonstration
En réalité, le théorème de Cauchy-Schwarz ne s’applique pas seulement aux produits scalaires, mais également aux formes bilinéaires positives. Notamment, on peut montrer que l’inégalité de Cauchy-Schwarz est également vraie pour la covariance.
On utilisera pour cela la première méthode, dressée plus haut.
Démonstration
Soit \( (X,Y) \) un couple de variables aléatoires d’un espace probabilisé quelconque.
- Si \( X=0 \) :
\[ Cov(X,Y)=0 \text{ et } V(X) \times V(Y)=0\]
Donc, l’inégalité et l’égalité sont vraies.
On suppose dans la suite que \( X \) et \( Y \) sont non nulles.
- On peut remarquer que :
\[ \forall \lambda \in \mathbb{R}, V(\lambda X+Y )^2 = Cov(X)^2 \lambda^2 + 2Cov(X,Y) \lambda + V(Y)^2 \]
Donc, \( P : \lambda \mapsto V(\lambda X+Y )^2 \) est une fonction polynôme, de degré 2 et à coefficients réels. De plus, par définition de \( P \) et parce que la variance est toujours positive, on a :
\[ \forall \lambda \in \mathbb{R}, P(\lambda) \ge 0 \]
Comme \( P \) est un polynôme de degré 2 à coefficients réels, on en déduit que \( P \) admet au plus une racine réelle, donc que son discriminant est négatif ou nul, c’est-à-dire :
\[ 4Cov(X,Y)^2 – 4V(X)^2 V(Y)^2 \le 0 \]
Et donc :
\[ Cov(X,Y)^2 \le V(X)^2 V(Y)^2 \]
Et comme la fonction \( t \mapsto \sqrt{t} \) est croissante sur \( \mathbb{R}^+ \) :
\[ \big| Cov(X,Y)\big| \le V(X) \cdot V(Y) \]
- Supposons maintenant que :
\[ \big| Cov(X,Y) \big| = V(X) \cdot V(Y) \]
On a alors :
\[ 4Cov(X,Y)^2 – 4V(X)^2 V(Y)^2 = 0 \]
Ce qui prouve que P admet une racine réelle \( \alpha \), et alors :
\[ Cov(\alpha X + Y) = 0 \]
Et donc :
\[ \alpha X + Y = 0 \]
Ce qui prouve que la famille \( (X,Y) \) est liée.
- Supposons enfin que la famille \( (X,Y) \) soit liée. Comme \( X \ne 0 \), il existe alors \( \alpha \in \mathbb{R} \) tel que : \( Y=\alpha X \) et alors :
\[ \big| Cov(X,Y) \big| = \big| \alpha \big| Cov(X,Y) \hspace{2pt} \text{ et } \hspace{2pt} V(X) V(Y) = \big| \alpha \big| V(X)^2 \]
Et donc :
\[ \big| Cov(X,Y) \big| = V(X)V(Y) \]
N’hésite pas à consulter toutes nos ressources mathématiques.