Dans cet article, on va revenir sur les questions d’informatique du sujet de concours suivant : Maths 2 HEC-ESCP ECS 2022. Les questions de Scilab ont été traduites en Python pour te permettre de t’entraîner en informatique. Tu peux utiliser cet article comme traduction de la partie Scilab du sujet d’origine, ou bien comme un exercice sur les thèmes de Python abordés par le sujet, à savoir : approximation d’une limite, calcul d’une somme, simulation de variables aléatoires, liste, histogramme et tracé de courbes.
Question 2.e)
✅ Cette question est faisable en première année.
❓ Énoncé
Pour tout \(n\geq1\), on pose \(S_n=\sum_{k=1}^n\frac1{k^2}\) et on admet qu’alors \((S_n)_{n\geq1}\) converge vers un réel \(S\) et que :
\[\frac1{n+1}\leq S-S_n\leq\frac1n\]
En déduire un programme Python qui permet d’obtenir une valeur approchée de \(S\) à \(10^{-7}\) près.
✏️ Corrigé
L’approximation de limites avec Python est quelque chose de très courant dans les sujets de concours.
Le principe est toujours le même : « \(S_n\) est une approximation à \(\varepsilon\) près de \(S\) » signifie que :
\[|S-S_n|\leq\varepsilon\]
Dans le cadre de cet exercice, l’énoncé choisit la précision \(\varepsilon=10^{-7}\), mais le raisonnement aurait été le même avec n’importe quel \(\varepsilon\) strictement positif.
Ensuite, il faut très souvent se servir d’un encadrement précédemment démontré.
Ici, on a montré que pour tout \(n\in\mathbb N^*\), \(\frac1{n+1}\leq S-S_n\), donc en particulier \(S-S_n\) est positif.
On peut donc oublier la valeur absolue : on cherche simplement une valeur de \(n\) telle que \(S-S_n\leq 10^{-7}\).
C’est là qu’on utilise l’autre partie de l’encadrement admis : pour \(n=10^7\), on obtient exactement :
\[S-S_{10^7}\leq 10^{-7}\]
Donc, \(S_{10^7}\) est une valeur approchée de \(S\) à \(10^7\) près. On calcule donc \(S_{10^7}\) avec Python :
Question 11.a)
✅ Cette question est faisable en première année.
❓ Énoncé
Soit \(n\in\mathbb N^*\). Pour tout \(i\in[\![ 1,n]\!]\), on note \(X_i\) une variable aléatoire qui suit la loi géométrique de paramètre \(\frac{n-i+1}n\).
On pose \(C_n=\sum_{i=1}^nX_i\), et \(V_n=\frac{C_n}n-\ln n\).
Écrire une fonction d’en-tête def simulV(n) qui, pour un entier \(n\) fourni en entrée, renvoie une simulation de la variable \(V_n\).
✏️ Corrigé
On procède étape par étape : d’abord, on simule \(C_n\), puis, à partir de cette simulation, on calcule la valeur de \(V_n\).
Pour calculer \(V_n\), nous allons avoir besoin de la fonction logarithme népérien \(\ln\). Attention : en Python la fonction logarithme népérien est notée log et non pas ln ! On l’importe donc : « from math import log ». Nous aurons aussi besoin de la fonction rd.geometric pour simuler une loi géométrique, d’où le « import numpy.random as rd ».
La variable \(C_n\) est une somme : comme dans tous les calculs de somme, on initialise une variable C avec la valeur 0.
Ensuite, on rajoute chaque terme un par un, grâce à une boucle for. Le \(i^{\text{ème}}\) terme de la somme doit être une simulation de la loi géométrique de paramètre \(\frac{n-i+1}n\), donc on rajoute à chaque fois rd.geometric((n-i+1)/n).
⚠️ Attention : dans la boucle for, il est impératif d’utiliser range(1,n+1). En effet, dans la définition de \(C_n\), l’indice \(i\) varie de \(1\) à \(n\), or, range(1,n+1) ne prend pas en compte la dernière valeur (ici \(n+1\)).
Une fois le calcul de la somme terminé (c’est-à-dire après la boucle for), on calcule \(V_n\) avec la définition.
Question 11.b)
✅ Cette question est faisable en première année.
❓ Énoncé
À la suite de la fonction simulV, écrire un programme Python qui construit un vecteur ligne V contenant \(1000\) simulations indépendantes de la variable aléatoire \(V_n\) pour un certain entier \(n\) entré par l’utilisateur.
✏️ Corrigé
Tout d’abord, l’entier \(n\) est entré par l’utilisateur : la ligne « n=int(input(‘Entrer un entier n:’)) » permet en une ligne de demander le nombre, puis de convertir le résultat (stocké en Python sous la forme de chaîne de caractères) en un entier, grâce à la fonction int.
C’est LA ligne de code à utiliser lorsque le programme doit demander un entier à l’utilisateur (remplacer int par float si c’est un réel).
Ensuite, il y a deux méthodes courantes : la liste vide et la liste nulle.
Méthode 1 : avec la liste vide
On crée une liste V, destinée à contenir les 1 000 simulations de \(V_n\). On l’initialise avec V = [ ]. Autrement dit, au départ, V est une « liste vide » : elle ne contient au départ aucun élément.
On va alors lui rajouter une par une les 1 000 simulations de \(V_n\) grâce à une boucle for, et grâce à la commande V.append, qui permet de rajouter un élément à la liste V.
Méthode 2 : avec la liste nulle
Dans cette méthode, on initialise V comme étant un vecteur ligne contenant 1 000 zéros, avec la commande np.zeros(1000) (en ayant préalablement importé numpy). Et au lieu d’ajouter des simulations, on va remplacer l’élément de V à la position \(k\) par une simulation de \(V_n\), pour tout \(k\) grâce à une boucle for.
Question 11.c)
❌ Cette question n’est pas faisable en première année.
❓ Énoncé
On admet que la fonction \(f:x\mapsto e^{-x}e^{-e^{-x}}\) est une densité de probabilité sur \(\mathbb R\). Lorsqu’une variable aléatoire \(X\) a pour densité \(f\), on dit que \(X\) suit la loi de Gumbel.
On complète le programme des questions précédentes par le code suivant :
On obtient les sorties graphiques suivantes en exécutant le programme pour \(n=5\), \(n=10\) puis \(n=50\) :
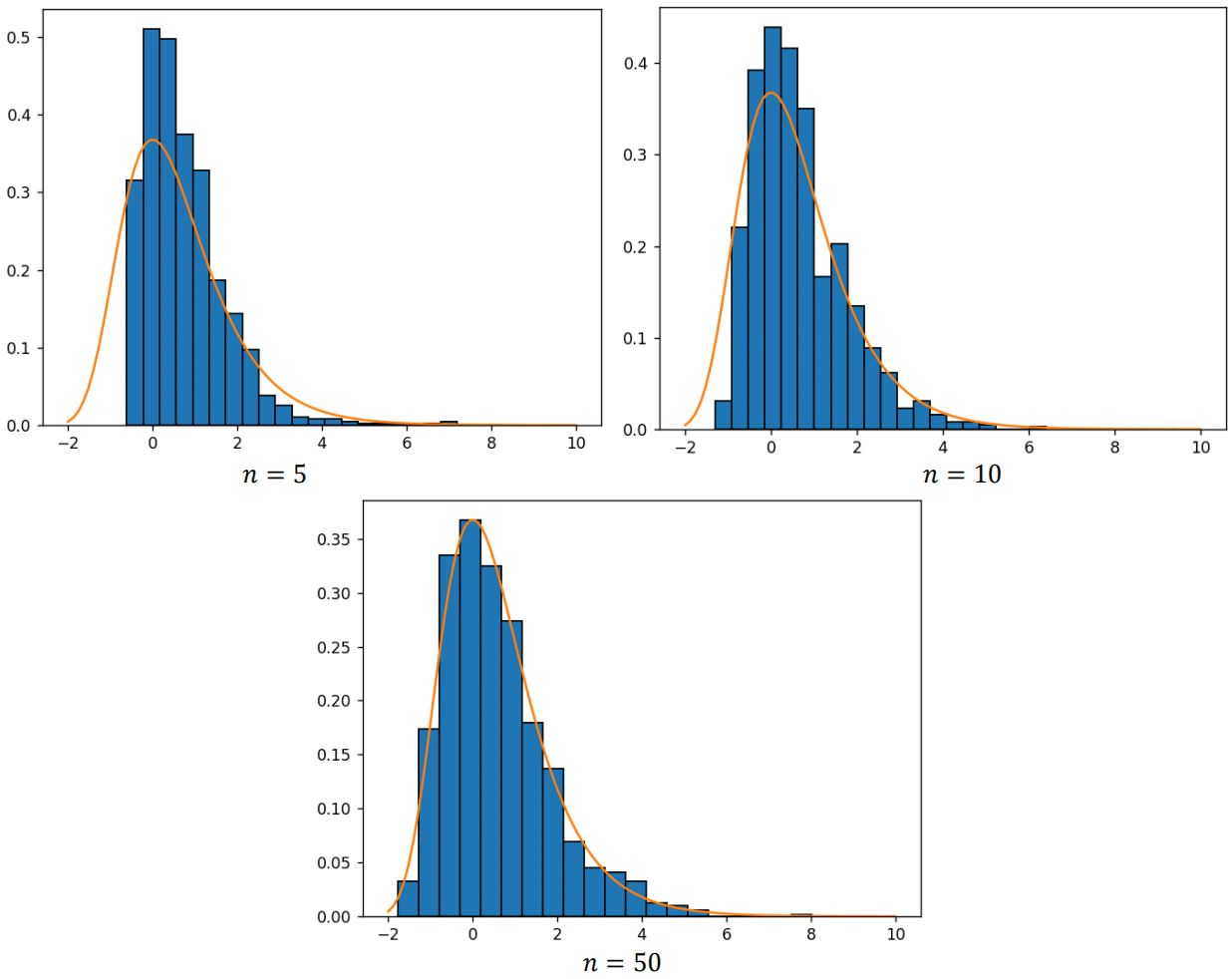
Que peut-on observer sur ces figures ? Quelle conjecture peut-on faire sur la suite \((V_n)_{n\geq 1}\) ?
✏️ Corrigé
Mis à part la ligne 4 qui construit l’histogramme, le reste du programme est un énorme classique. C’est LE programme pour tracer la courbe d’une fonction (ici : la fonction \(f\) sur l’intervalle \([-2,10]\)). Apprends-le par cœur !
Je t’explique dans le détail ce que fait ce programme, pour que tu puisses le reproduire :
- Lignes 1-3 : on importe l’exponentielle, le module pour tracer les courbes et les histogrammes, et le module numpy.
- Ligne 4 : on trace un histogramme en 20 classes représentant la répartition de V. L’option « density=True » permet que la hauteur de chaque bâton soit égale à la proportion des simulations de \(V_n\) qui sont dans cette classe (« edgecolor=’k’ » n’est pas très important, c’est juste pour que le contour des bâtons soit en noir).
- Lignes 5-6 : on crée la fonction \(f:x\mapsto e^{-x}e^{-e^{-x}}\).
- Ligne 7 : on construit un vecteur X qui va représenter les abscisses. La commande np.linspace(-2,10,100) renvoie un vecteur ligne contenant 100 réels équitablement répartis dans l’intervalle \([-2,10]\). Le nombre 100 est un nombre pensé comme un « grand » nombre. En effet, on ne peut pas vraiment représenter l’intervalle \([-2,10]\), car il contient une infinité de nombres. Donc, on crée un vecteur qui « ressemble » à cet intervalle, car il contient beaucoup de nombres, pour tracer la courbe avec ces nombres en abscisses.
- Ligne 8 : [f(x) for x in X] permet de créer une liste qui contient toutes les images des éléments de X par la fonction \(f\). Pour chaque élément x de X, on calcule son image par la fonction f et on le place dans la liste.
- Ligne 9 : on trace la courbe qui relie les points (X[k],Y[k]). Autrement dit, étant donné la façon dont on a construit Y, les points \((x,f(x))\) pour tout \(x\) appartenant à X. C’est donc la courbe de la fonction \(f\) qu’on est en train de tracer.
- Ligne 10 : on affiche, sur le même graphique, l’histogramme et la courbe.
Dans le cadre de cet exercice, une fois qu’on a compris qu’on affiche l’histogramme de V et la courbe de \(f\), c’est surtout les graphiques affichés qui nous intéressent.
On observe que plus \(n\) est grand, plus les bâtons ont une hauteur proche de la courbe de \(f\).
On conjecture donc que \(V_n\) converge en loi vers une loi de Gumbel.
Conclusion
Voici les techniques qu’il faut retenir à l’issue de ces quelques questions de Maths 2 2022 :
- Comprendre la théorie derrière l’approximation de la limite (que signifie « \(S_n\) est une approximation à \(\varepsilon\) près de \(S\) » ?) et également la façon dont on calcule cette approximation en Python, en exploitant l’encadrement de \(|S_n-S|\).
- Connaître les commandes pour simuler les lois de variables aléatoires classiques (loi géométrique, loi uniforme, loi de Poisson, etc.).
- Comprendre les deux méthodes pour créer un vecteur de simulations, et savoir reproduire au moins l’une des deux.
- Savoir reproduire le programme type pour afficher la courbe d’une fonction en Python.
- Savoir reconnaître, lorsqu’on superpose histogramme et courbe de densité, une convergence en loi.