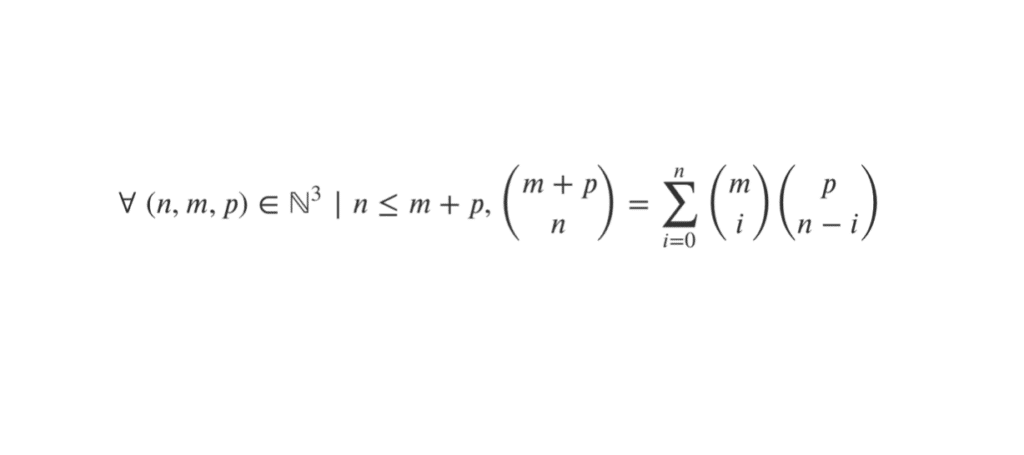Certaines formules mathématiques se démarquent par leur importance et leur utilité. L’une de ces égalités est la formule de Vandermonde, qui trouve des applications dans divers domaines tels que l’algèbre, la combinatoire et la théorie des probabilités. Dans cet article, je te présente cette formule remarquable ainsi que deux démonstrations hors programme qui te seront utiles aux épreuves parisiennes.
La formule de Vandermonde expliquée en français
Cette formule, développée par le mathématicien français Alexandre-Théophile Vandermonde, établit une égalité entre un coefficient binomial et une somme de produits de coefficients binomiaux.
Il existe de nombreuses manières de la démontrer, ce qui renforce son importance et son utilité.
La formule
Si \( n, m, p\) sont des entiers avec \( n \le m + p \), alors : \(\displaystyle {{m+p}\choose{n}}=\sum^n_{i=0} {{m}\choose{i}} {{p}\choose{n-i}}\)
Démonstration de la formule de Vandermonde par le calcul
La formule de Vandermonde peut être démontrée de manière algébrique en considérant le polynôme \( P=(1+X)^{m+p}=(1+X)^m(1+X)^p \) avec \( (m,p) \in \mathbb{N}^2 \)
\( \text{Premièrement : } (1+X)^{m+p}=\displaystyle \sum_{i=0}^{m+p} {{m+p}\choose{i}} X^i\) (application du binôme de Newton)\(
\begin{align}
\text{Deuxièmement : } (1+X)^m(1+X)^p &= \left ( \sum_{i=0}^{m} {{m}\choose{i}} X^i \right )\left ( \sum_{j=0}^{p} {{p}\choose{j}} X^j \right )\\
&=\ \sum^m_{i=0} \sum^p_{j=0} {{m}\choose{i}} {{p}\choose{j}} X^{i+j} \\
&=\sum^{m+p}_{k=0} \sum_{i+j=k} {{m}\choose{i}} {{p}\choose{j}} X^{i+j} \\
&= \sum^{m+p}_{k=0} \left( \sum_{i=0}^k {{m}\choose{i}} {{p}\choose{k-i}}\right)X^{k}
\end{align}
\)
N.B. : Si tu ne comprends pas le passage de la deuxième ligne à la troisième ligne au niveau des indices de sommation, va jeter un œil sur la huitième astuce de cet article sur les sommes.
Maintenant, étudions le coefficient en \( X^n \) de ces deux expressions. D’un côté, nous trouvons \( \displaystyle {{m+p}\choose{n}}\) et de l’autre, \( \displaystyle \sum_{i=0}^n {{m}\choose{i}} {{p}\choose{n-i}}\). Or, les coefficients d’un polynôme sont uniques.
D’où : \( \fbox{\(\displaystyle {{m+p}\choose{n}}=\sum^n_{i=0} {{m}\choose{i}} {{p}\choose{n-i}}\)} \)
Démonstration de la formule de Vandermonde par dénombrement
Premièrement, considérons un ensemble \( E \) à \( m + p \) éléments.
Le coefficient binomial \( \displaystyle {{m+p}\choose{n}} \) représente le nombre de façons de choisir \(n\) éléments distincts dans \(E\).
Cependant, nous pouvons calculer le nombre de façons de choisir \(n\) éléments distincts dans \(E\) avec une autre méthode. En effet, considérons un sous-ensemble de \(E\), qu’on notera \(M\) (avec \(m\) éléments), et son complémentaire, qu’on notera \(P\) (avec \(p\) éléments).
Nous pouvons fixer \(i\) dans \([\![0,m+p]\!]\) et choisir d’abord \(i\) éléments dans \(M\), puis \(n-i\) éléments dans \(P\). Ainsi, le nombre de façons de choisir \(n\) éléments distincts dans \(E\) vaut \( \displaystyle \sum_{i=0}^n {{m}\choose{i}} {{p}\choose{n-i}}\).
D’où : \( \fbox{\(\displaystyle {{m+p}\choose{n}}=\sum^n_{i=0} {{m}\choose{i}} {{p}\choose{n-i}}\)} \)
Un cas particulier de la formule de Vandermonde
Soit \( (n, m, p) \in \mathbb{N}^3 \; | \; n=m=p,\) en utilisant le fait que \( \forall i \in [\![0,n]\!], \; \displaystyle {{n}\choose{i}} = {{n}\choose{n-i}} \), nous obtenons une autre formule remarquable :
\[ \fbox{ \( \displaystyle {{2n}\choose{n}}=\sum^n_{i=0} {{n}\choose{i}}^2 \)} \]
Cette nouvelle égalité est étroitement liée à des problèmes de la théorie des nombres tels que les coefficients binomiaux centrés.
Conclusion
La formule de Vandermonde est un outil mathématique précieux avec des démonstrations diverses. Bien que hors programme, sa compréhension approfondie enrichira ta préparation aux épreuves des écoles parisiennes.
Tu peux retrouver ici toutes nos autres ressources mathématiques !