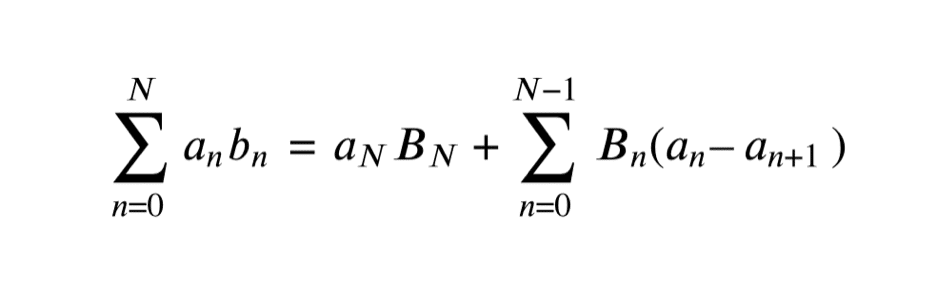La transformation d’Abel, également connue sous le nom de formule de sommation par parties, ou sommation d’Abel, est un instrument mathématique d’analyse particulièrement puissant. Cette méthode permet de convertir une somme de produits de suites finies en d’autres expressions, facilitant souvent les calculs et ouvrant la voie à l’estimation de divers types de sommes. C’est également une analogie discrète de l’intégration par parties qui est au programme d’ECG. Cette formule de sommation par parties trouve sa place fondamentale dans le critère d’Abel, qui offre une approche pour établir la convergence de certaines séries. Nous allons explorer plus en détail cette transformation ainsi que ce critère pour enrichir ta préparation aux épreuves parisiennes et aux oraux de mathématiques.
La transformation d’Abel
Soient \( (a_n)_{n \in \mathbb{N}} \; \text{et} \; (b_n)_{n \in \mathbb{N}} \; \text{dans} \; \mathbb{R}^{\mathbb{N}} \), la transformation d’Abel s’écrit sous la forme :
\[ \forall N \in \mathbb{N}, \;\displaystyle \sum_{n=0}^{N} a_n b_n = a_0 b_0 + a_N B_N – a_1 b_0 + \sum_{n=1}^{N-1} B_n ( a_n – a_{n+1} ) \; \text{où} \; B_N = \sum_{n=0}^Nb_n \]
Nous pouvons également écrire cette formule sous la forme suivante :
\[ \forall N \in \mathbb{N}, \;\displaystyle \sum_{n=0}^{N} a_n b_n = a_NB_N + \sum_{n=0}^{N-1} B_n ( a_n – a_{n+1} ) \; \text{où} \; B_N = \sum_{n=0}^Nb_n \]
Il existe également une dernière manière d’écrire cette propriété, qui peut s’avérer particulièrement utile dans certains exercices :
\[ \displaystyle \sum_{k=0}^{N-1} \left( a_{k+1} – a_k \right) b_k = (a_N b_N – a_0 b_0) – \sum_{k=0}^{N-1} a_{k+1} \left( b_{k+1} – b_k \right) \]
Démonstration
La démonstration de la transformation d’Abel, bien que hors programme, mérite un regard attentif pour en saisir toute la portée. En étoffant notre compréhension de la démonstration, nous renforçons notre capacité à appliquer cette puissante formule dans des contextes variés. La démonstration présentée précédemment offre un aperçu succinct.
Plongeons davantage dans les subtilités de chaque étape pour mieux appréhender la logique qui sous-tend cette transformation. De plus, si tu es amené(e) à utiliser cette propriété lors des écrits ou des oraux, il est fort probable que le sujet te fasse démontrer cette formule comme dans la question 9. b) du sujet Maths I 2014 (mathématiques approfondies). D’où l’intérêt de connaître cette démonstration.
Soit \( N \in \mathbb{N}, \)
\(
\begin{align}
\displaystyle \sum_{n=0}^N a_n b_n &= a_0 b_0 + \sum_{n=1}^N a_n b_n \\
&= a_0 b_0 + \sum_{n=1}^N a_n ( B_n – B_{n-1} ) \\
&= \displaystyle a_0 b_0 + \sum_{n=1}^N a_n B_n – \sum_{n=1}^N a_n B_{n-1} \\
&= \displaystyle a_0 b_0 + \sum_{n=1}^N a_n B_n – \sum_{n=0}^{N-1} a_{n+1} B_n \\
&= \displaystyle a_0 b_0 + a_N B_N + \sum_{n=1}^{N-1} a_n B_n – a_1 B_0 – \sum_{n=1}^{N-1} a_{n+1} B_n\\
&= \displaystyle a_0 b_0 + a_N B_N – a_1 B_0 + \sum_{n=1}^{N-1} B_n ( a_n – a_{n+1} ) \\
&= \displaystyle a_0 B_0 + a_N B_N – a_1 B_0 + \sum_{n=1}^{N-1} B_n ( a_n – a_{n+1} ) \\
&= \displaystyle a_N b_N + \sum_{n=0}^{N-1} B_n ( a_n – a_{n+1} )
\end{align}
\)
Exemple d’utilisation de la formule
Appliquons le résultat de la sommation par parties pour obtenir un résultat au programme. C’est-à-dire une expression de \( \displaystyle \sum_{k=0}^{n-1} k x^k : \)
\(
\begin{align}
\displaystyle ( x – 1 ) \sum_{k=0}^{n-1} k x^k &= \sum_{k=0}^{n-1} k ( x^{k+1} – x^k ) \\
&= \displaystyle \sum_{k=0}^N 1 \times x^k – n x^n \\
&= \displaystyle \frac{1 – x^{n+1}}{1-x} – n x^n \\
&= \displaystyle \frac{1 – x^{n+1} – n x^n + n x^{n+1}}{1-x} \\
&= \displaystyle \frac{ x^{n+1} ( n – 1 ) – n x^n + 1 }{ 1 – x }
\end{align}
\)
D’où : \( \displaystyle \sum_{k=0}^{n-1} k x^k = \frac{ x^{n+1} ( n – 1 ) – n x^n + 1 }{ ( 1 – x )^2 } \)
Il faut réussir à identifier les suites \( a \; \text{et} \; {b} \) qui ici sont respectivement les suites \( (x^n)_{n \in \mathbb{N}} \; \text{et} \; (1)_{n \in \mathbb{N}}. \)
L’analogie avec l’intégration par parties
L’analogie entre la transformation d’Abel et l’intégration par parties élargit notre vision des outils mathématiques. Alors que l’intégration par parties se concentre sur la continuité, la transformation d’Abel opère dans le domaine discret des séries. Comprendre cette relation nous offre une perspective plus holistique sur la manière dont ces méthodes s’influencent mutuellement.
La formule d’intégration par parties au programme s’écrit de cette manière : \( \displaystyle \int_{a}^{b} f'(x)g(x) \, \mathrm{d}x = \left[ f(x)g(x) \right]_{a}^{b} – \int_{a}^{b} f(x)g'(x) \, \mathrm{d}x \)
Ainsi, nous pouvons comprendre que l’intégration par parties consiste à intégrer une des deux fonctions présentes dans l’intégrale initiale et à dériver l’autre : on passe de \( f^{\prime} \; \text{à} \; f \) et de \( g \; \text{à} \; g^{\prime}. \) La transformation d’Abel consiste à réaliser une transformation analogue, mais discrète : on passe de \( a_{n+1} – a_n \; \text{à} \; a_n \) et de \( b_n \; \text{à} \; b_{n+1} – b_n.\)
Le critère d’Abel
Le critère de convergence d’Abel est un résultat qui se démontre à l’aide d’une majoration astucieuse dans la formule de la transformation d’Abel. Voici son énoncé :
Si la suite \( (a_n)_{ n \in \mathbb{N} } \) tend vers 0 et la suite \( (B_n)_{ n \in \mathbb{N} } \) est bornée, et si la série \( \displaystyle \sum ( a_{n+1} – a_{n} ) \) est absolument convergente, alors la série \( \displaystyle \sum ( a_n b_n ) \) est convergente.
Le théorème d’Abel
Il arrive souvent d’entendre parler du théorème d’Abel qui fait référence à un cas particulier du critère de convergence d’Abel.
Si la suite \( (a_n)_{ n \in \mathbb{N} } \) est monotone et de limite nulle et si la suite \( (B_n)_{ n \in \mathbb{N} } \) est bornée, alors la série \( \displaystyle \sum ( a_n b_n ) \) est convergente.
Conclusion
En somme, la transformation d’Abel se révèle être un outil mathématique d’une grande puissance analytique. Cette méthode, également appelée formule de sommation par parties ou sommation d’Abel, offre une approche discrète équivalente à l’intégration par parties, enrichissant ainsi notre compréhension des séries mathématiques.
L’introduction du critère d’Abel et du théorème associé apporte une dimension pratique en permettant d’établir la convergence de certaines séries, offrant ainsi une perspective essentielle pour les étudiants préparant les épreuves parisiennes et les oraux de mathématiques. En examinant de plus près la transformation d’Abel et ses applications, les mathématiciens sont équipés d’un outil élégant pour simplifier les calculs et explorer la convergence des séries, soulignant ainsi son importance dans le paysage mathématique.
Pour appliquer les résultats que nous venons d’étudier, tu peux t’entraîner sur le sujet Maths I 2014 (mathématiques approfondies) qui aborde la transformation d’Abel.
Tu peux retrouver ici toutes nos autres ressources mathématiques !