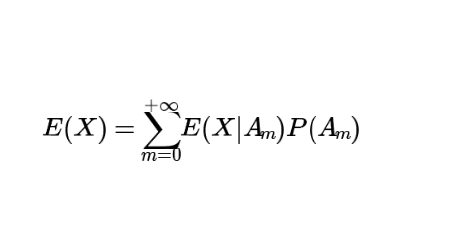L’espérance conditionnelle est un concept fondamental en probabilité et en statistique, particulièrement utile dans l’analyse des variables aléatoires dépendantes. Elle permet de calculer l’espérance d’une variable aléatoire en tenant compte de l’information partielle disponible. Cet article explore la notion de variables et d’espérance conditionnelle, en introduisant les concepts clés et en illustrant leur utilisation par des exemples concrets.
L’objectif de cet article est de découvrir la notion d’espérance conditionnelle, qui peut être très utile dans certains exercices. Elle peut être retrouvée dans des sujets de tous types. Cet article se limite à l’étude de l’espérance conditionnelle pour les variables aléatoires réelles. L’étude de l’espérance conditionnelle pour les variables aléatoires discrètes est bien au-delà du programme.
Espérance Mathématique
L’espérance mathématique, ou moyenne, d’une variable aléatoire \(X\), notée \(\mathbb{E}[X]\), est une mesure de la valeur moyenne que \(X\) prendrait si l’expérience aléatoire était répétée un grand nombre de fois. Pour une variable aléatoire discrète \(X\) prenant des valeurs \(x_1, x_2, \ldots\) avec des probabilités associées \(p_1, p_2, \ldots\), l’espérance est définie par :
\[ \mathbb{E}[X] = \sum_{i} x_i p_i \]
Pour une variable aléatoire continue avec une densité de probabilité \(f_X(x)\), l’espérance est donnée par :
\[ \mathbb{E}[X] = \int_{-\infty}^{\infty} x f_X(x) \, dx \]
Espérance Conditionnelle
Dans le cas discret, l’espérance conditionnelle d’une variable aléatoire \(X\) notée \(\mathbb{E}[X \mid \mathcal{G}]\), est une variable aléatoire qui représente la meilleure estimation de \(X\) compte tenu de l’information contenue dans \(\mathcal{G}\). Plus précisément, si \(\mathcal{G}\) est générée par une partition \(\{A_1, A_2, \ldots, A_n\}\) de l’espace \(\Omega\), alors l’espérance conditionnelle de \(X\) donnée \(\mathcal{G}\) est définie par :
\[ \mathbb{E}[X \mid \mathcal{G}](\omega) = \sum_{i=1}^n \mathbb{E}[X \mid A_i] \mathbf{1}_{A_i}(\omega) \]
où \(\mathbf{1}_{A_i}\) est la fonction indicatrice de l’événement \(A_i\), et \(\mathbb{E}[X \mid A_i]\) est l’espérance conditionnelle de \(X\) sur l’événement \(A_i\).
Cette approche permet de décomposer l’espérance conditionnelle en une somme pondérée des espérances conditionnelles sur les événements de la partition, reflétant ainsi l’information disponible dans \(\mathcal{G}\).
Définition
L’espérance conditionnelle d’une variable aléatoire réelle donne la valeur moyenne de cette variable quand un certain événement est réalisé. L’espérance de la variable aléatoire \(X\) conditionnée par l’événement \(B\) se note \(E(X|B)\). On peut également définir l’espérance conditionnelle d’une variable aléatoire \(X\) par rapport à une autre variable aléatoire \(Y\), on notera de même \(E(X|Y)\).
Soit \(X\) une variable aléatoire discrète, on note \(X(\Omega)={x_k}\) avec \(k\) un entier naturel.
Si \(B\) est un événement de probabilité non nulle, sous réserve d’absolue convergence, on appelle « espérance conditionnelle de \(X\) » : \(E(X|B)=\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)\)
Exemples d’Espérance Conditionnelle
Considérons un exemple simple où nous avons une variable aléatoire discrète \(X\) prenant des valeurs \(1, 2, 3\) avec des probabilités respectives \(0.2, 0.5, 0.3\), et une autre variable aléatoire \(Y\) définie par :
\[ Y = \begin{cases}
1 & \text{si } X \in \{1, 2\} \\
2 & \text{si } X = 3
\end{cases} \]
Pour déterminer l’espérance conditionnelle de \(X\) donnée \(Y\), notée \(\mathbb{E}[X \mid Y]\), nous utilisons la définition et les propriétés des probabilités conditionnelles :
- \(\mathbb{E}[X \mid Y = 1] = \mathbb{E}[X \mid X \in \{1, 2\}] = 1 \cdot \frac{0.2}{0.7} + 2 \cdot \frac{0.5}{0.7} = \frac{0.2 + 1}{0.7} = \frac{1.2}{0.7} \approx 1.71\)
- \(\mathbb{E}[X \mid Y = 2] = \mathbb{E}[X \mid X = 3] = 3\)
Ainsi, nous avons :
\[ \mathbb{E}[X \mid Y] = \begin{cases}
\frac{1.2}{0.7} \approx 1.71 & \text{si } Y = 1 \\
3 & \text{si } Y = 2
\end{cases} \]
Propriétés de l’Espérance Conditionnelle
L’espérance conditionnelle possède plusieurs propriétés importantes :
Linéarité : Pour des variables aléatoires \(X\) et \(Y\) et des constantes \(a\) et \(b\), \(\mathbb{E}[aX + bY \mid \mathcal{G}] = a\mathbb{E}[X \mid \mathcal{G}] + b\mathbb{E}[Y \mid \mathcal{G}]\).
Loi de l’Espérance Totale : \(\mathbb{E}[\mathbb{E}[X \mid \mathcal{G}]] = \mathbb{E}[X]\).
Prise en compte de l’information : Si \(X\) ne dépend pas de \(\mathcal{G}\), alors \(\mathbb{E}[X \mid \mathcal{G}] = \mathbb{E}[X]\).
Invariance par rapport aux événements de \(\mathcal{G}\) : Pour tout \(A \in \mathcal{G}\), \(\mathbb{E}[X \mathbf{1}_A \mid \mathcal{G}] = \mathbf{1}_A \mathbb{E}[X \mid \mathcal{G}]\).
Démonstrations des propriétés
1 – L’espérance conditionnelle est linéaire : Soit \((a,b)\) un couple de réel et soit \((X,Y)\) un couple de variables aléatoires réelles. Soit \(B\) un événement. \(E(aX+bY|B)=aE(X|B)+bE(Y|B)\)
Démonstration
Soit \(X\) une variable aléatoire réelle, \(a\) un réel et \(B\) un événement de probabilité non nulle. \(E(aX|B)=\displaystyle \sum_{k=0}^{+\infty}
ax_kP_B(X=x_k)=a\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)=aE(X|B)\)
2 – Si \(X\) est indépendant de l’événement \(B\), alors \(E(X|B)=E(X)\)
Démonstration
Soit \(X\) une variable aléatoire réelle et \(B\) un événement de probabilité non nulle tel que \(X\) et \(B\) soient indépendants. \(E(X|B)=\displaystyle \sum_{k=0}^{+\infty}
x_kP_B(X=x_k)=\displaystyle \sum_{k=0}^{+\infty}
x_kP(X=x_k)=E(X)\)
3 – L’espérance conditionnelle est croissante : si \(X\le Y\), alors \(E(X|B) \le E(Y|B)\)
Calcul de l’Espérance Conditionnelle dans un Cas Discret
Pour illustrer le calcul de l’espérance conditionnelle dans un cas discret, considérons un exemple concret avec deux variables aléatoires discrètes \(X\) et \(Y\) définies sur un espace probabilisé \((\Omega, \mathcal{F}, \mathbb{P})\). Supposons que \(X\) prenne les valeurs \(\{1, 2, 3\}\) et \(Y\) prenne les valeurs \(\{A, B\}\). La probabilité jointe de \(X\) et \(Y\) est donnée par :
- \(\mathbb{P}(X = 1 \cap Y = A) = 0.1\)
- \(\mathbb{P}(X = 2 \cap Y = A) = 0.3\)
- \(\mathbb{P}(X = 3 \cap Y = A) = 0.2\)
- \(\mathbb{P}(X = 1 \cap Y = B) = 0.2\)
- \(\mathbb{P}(X = 2 \cap Y = B) = 0.1\)
- \(\mathbb{P}(X = 3 \cap Y = B) = 0.1\)
Nous voulons calculer l’espérance conditionnelle de \(X\) donnée \(Y\), c’est-à-dire \(\mathbb{E}[X \mid Y]\). Pour cela, nous devons d’abord déterminer la distribution conditionnelle de \(X\) sachant \(Y = A\) et \(Y = B\). Utilisons les définitions des probabilités conditionnelles :
Pour \(Y = A\), les probabilités conditionnelles de \(X\) sont :
\[ \mathbb{P}(X = 1 \mid Y = A) = \frac{\mathbb{P}(X = 1 \cap Y = A)}{\mathbb{P}(Y = A)} = \frac{0.1}{0.6} = \frac{1}{6} \]
\[ \mathbb{P}(X = 2 \mid Y = A) = \frac{0.3}{0.6} = \frac{1}{2} \]
\[ \mathbb{P}(X = 3 \mid Y = A) = \frac{0.2}{0.6} = \frac{1}{3} \]
où \(\mathbb{P}(Y = A) = 0.1 + 0.3 + 0.2 = 0.6\).
Pour \(Y = B\), les probabilités conditionnelles de \(X\) sont :
\[ \mathbb{P}(X = 1 \mid Y = B) = \frac{\mathbb{P}(X = 1 \cap Y = B)}{\mathbb{P}(Y = B)} = \frac{0.2}{0.4} = \frac{1}{2} \]
\[ \mathbb{P}(X = 2 \mid Y = B) = \frac{0.1}{0.4} = \frac{1}{4} \]
\[ \mathbb{P}(X = 3 \mid Y = B) = \frac{0.1}{0.4} = \frac{1}{4} \]
où \(\mathbb{P}(Y = B) = 0.2 + 0.1 + 0.1 = 0.4\).
Ensuite, nous utilisons ces probabilités conditionnelles pour calculer l’espérance conditionnelle de \(X\) donnée \(Y\). Pour \(Y = A\), nous avons :
\[ \mathbb{E}[X \mid Y = A] = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{2} + 3 \cdot \frac{1}{3} = \frac{1}{6} + 1 + 1 = \frac{1}{6} + \frac{6}{6} + \frac{6}{6} = \frac{13}{6} \approx 2.17 \]
Pour \(Y = B\), nous avons :
\[ \mathbb{E}[X \mid Y = B] = 1 \cdot \frac{1}{2} + 2 \cdot \frac{1}{4} + 3 \cdot \frac{1}{4} = \frac{1}{2} + \frac{2}{4} + \frac{3}{4} = \frac{1}{2} + \frac{5}{4} = \frac{2}{4} + \frac{5}{4} = \frac{7}{4} = 1.75 \]
Ainsi, l’espérance conditionnelle de \(X\) donnée \(Y\) est :
\[ \mathbb{E}[X \mid Y] = \begin{cases}
\frac{13}{6} \approx 2.17 & \text{si } Y = A \\
1.75 & \text{si } Y = B
\end{cases} \]
Cette méthode montre comment l’espérance conditionnelle peut être calculée en utilisant les probabilités conditionnelles et les valeurs de la variable aléatoire \(X\) dans le cas discret. Elle illustre également l’importance de connaître les distributions conjointes et conditionnelles pour réaliser ces calculs de manière précise.
Espérance Conditionnelle et Processus de Markov
Les processus de Markov constituent une autre application importante de l’espérance conditionnelle. Un processus stochastique \((X_t)_{t \geq 0}\) est un processus de Markov si, pour tout \(s < t\) et pour toute fonction \(g\), nous avons :
\[ \mathbb{E}[g(X_t) \mid \mathcal{F}_s] = \mathbb{E}[g(X_t) \mid X_s] \]
En d’autres termes, la distribution conditionnelle de \(X_t\) étant donné le passé \(\mathcal{F}_s\) ne dépend que de l’état actuel \(X_s\). Cette propriété de Markov, appelée propriété d’absence de mémoire, simplifie considérablement l’analyse des processus stochastiques et est utilisée dans de nombreux domaines, y compris les chaînes de Markov, les processus de Poisson et les modèles de file d’attente.
Par exemple, considérons une chaîne de Markov à temps discret avec des états \(\{1, 2, 3\}\) et une matrice de transition :
\[ P = \begin{pmatrix} 0.1 & 0.6 & 0.3 \\ 0.4 & 0.4 & 0.2 \\ 0.2 & 0.3 & 0.5 \end{pmatrix} \]
Si l’état actuel est \(X_0 = 2\), l’espérance conditionnelle de l’état au temps \(t=1\) est donnée par :
\[ \mathbb{E}[X_1 \mid X_0 = 2] = \sum_{j=1}^3 j P_{(2,j)} = 1 \cdot 0.4 + 2 \cdot 0.4 + 3 \cdot 0.2 = 1.8 \]
Formule de l’espérance totale
Connaître l’espérance conditionnelle d’une variable aléatoire peut nous permettre de trouver son espérance.
Soit \(X\) une variable aléatoire discrète, on note \(X(\Omega)={x_k}\) avec \(k\) un entier naturel.
Soit \({A_m}\) avec \(m \in \mathbb{N}\) un système complet d’événement de \(\Omega\) tel que \(\forall m \in
\mathbb{N}, P(A_m) \le 0\)
Alors, \(X\) admet une espérance si et seulement si la série \(\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\) converge absolument. Dans ce cas, on a \(E(X)=\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\)
Démonstration
\(\begin{align}
E(X) \; \text{existe} & \Leftrightarrow \sum_{n \ge 0} x_nP(X=x_n) \; \text{converge absolument} \\
&\Leftrightarrow \sum_{n \ge 0} x_n(\sum_{m \ge 0} P(A_m)P_{A_m}(X=x_n) ) \;\text{converge absolument} \\
&\Leftrightarrow \sum_{n \ge 0} \sum_{m \ge 0} x_nP(A_m)P_{A_m}(X=x_n) \; \text{converge absolument}\\
&\Leftrightarrow \sum_{m \ge 0} \sum_{n \ge 0} x_nP_{A_m}(X=x_n)P(A_m) \; \text{converge absolument} \\
&\Leftrightarrow \sum_{m \ge 0} E(X|A_m)P(A_m) \;\text{converge absolument}
\end{align}\)
Ainsi en cas d’absolue convergence, on retrouve bien : \(E(X)=\displaystyle \sum_{m=0}^{+\infty}
E(X|A_m)P(A_m)\)
Exemple avec un dé
On lance un dé équilibré à six faces. On considère deux variables aléatoires \(A\) et \(B\) telles que \(A\) vaut \(1\) quand le résultat du lancer est pair (\(A(\Omega)=(2,4,6)\)) et \(0\) sinon. \(B\) vaut \(1\) quand le résultat est un nombre premier \((B(\Omega)=(2,3,5))\) et \(0\) sinon.

L’espérance (non conditionnelle) de \(A\) vaut \(E(A)=\frac{3}{6}=\frac{1}{2}\)
L’espérance de \(A\) conditionnée à l’événement \([B=1]\) vaut \(E(A|B=1)=(1+0+0)/3=1/3\)
L’espérance de \(B\) conditionnée à l’événement \([A=0]\) vaut \(E(B|A=0)=(0+1+1)/3=2/3\)
Exemple avec des lois classiques
On lance un dé équilibré, le résultat est une variable aléatoire \(X\). \(X \hookrightarrow
\mathcal{U}([\![1,6]\!])\). On pose alors \(Y \hookrightarrow
\mathcal{U}([\![1,X]\!])\). Déterminons \(E(Y)\).
\(E(Y)=\displaystyle \sum_{n=1}^{6}E(Y|X=n)P(X=n)=\displaystyle \sum_{n=1}^{6}\displaystyle \sum_{k=1}^{n}kP_{X=n}(Y=k)P(X=n) =\displaystyle \sum_{n=1}^{6}\displaystyle \sum_{k=1}^{n} k\frac{1}{n}\frac{1}{6}=\displaystyle \sum_{n=1}^{6} \frac{1}{6n}\frac{n(n+1)}{2}=\frac{27}{12}\).
Conclusion
L’espérance conditionnelle est un outil puissant qui permet d’affiner notre compréhension des variables aléatoires en fonction de l’information disponible. En offrant une manière de calculer des espérances en tenant compte de nouvelles informations, elle est essentielle pour de nombreuses applications pratiques en statistique, en finance et en sciences. Maîtriser ce concept permet d’approfondir l’analyse probabiliste et d’améliorer les modèles prédictifs dans divers domaines. Ainsi, bien que cette notion soit hors programme, une compréhension approfondie de ses propriétés te permettra de te préparer aux épreuves parisiennes et notamment au Maths II.
Pour t’entrainer sur cette notion tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies)
- Maths II 2009 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !