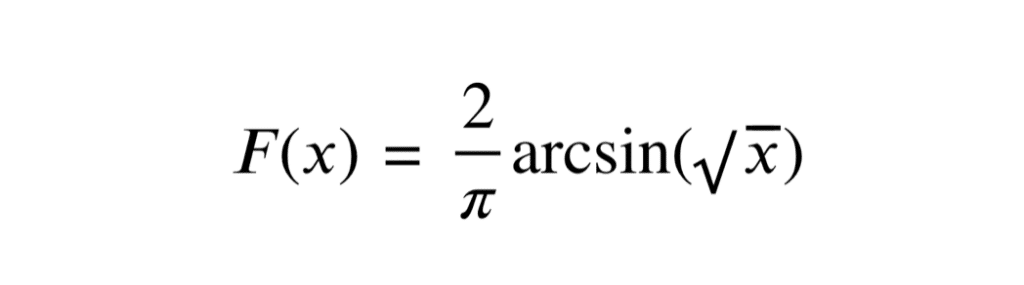Nous allons étudier la loi arc sinus standard. Elle constitue une distribution de probabilité essentielle dans le domaine des probabilités et en analyse. Caractérisée par une fonction de répartition avec une fonction trigonométrique, elle offre une perspective unique sur la modélisation de marches aléatoires. Cette loi correspond également à un cas particulier de la loi Bêta, un classique dans le domaine des probabilités. Dans cet article, nous explorerons les propriétés fondamentales de la loi arc sinus standard, de sa densité à son espérance, en mettant en lumière son lien intéressant avec la loi uniforme, tout en considérant une généralisation de cette loi à support borné. Bien que cette notion soit hors programme, il te sera particulièrement utile de maîtriser les propriétés ci-dessous pour les épreuves parisiennes ainsi que pour les oraux de mathématiques.
La loi arc sinus standard
Une variable aléatoire \(X\) suit la loi arc sinus standard à condition que sa fonction de répartition soit donnée par : \( \displaystyle \fbox{ \( \forall x \in [0,1], \; F(x) = \displaystyle \frac{2}{\pi} \arcsin(\sqrt{x}). \)} \)
Notons que le support de cette variable est \([0,1].\)
Il est particulièrement important et utile de savoir retrouver la densité à partir de la fonction de répartition, car c’est une question classique aux écrits et aux oraux de mathématiques. De plus, la démonstration fait intervenir plusieurs propriétés trigonométriques fondamentales. L’une des propriétés est la dérivée de \(\arcsin\), que nous allons maintenant calculer à l’aide de la formule de dérivée de la réciproque d’une fonction.
\( \forall x \in ]-1,1[, \; \arcsin^{\prime}(x) =\displaystyle \frac{1}{\sin^{\prime}(\arcsin(x))} =\frac{1}{\cos(\arcsin(x))} \)
Il faut désormais réussir à calculer \( \cos(\arcsin(x)), \), une question très classique dans les sujets HEC. Il faut utiliser l’identité : \( \cos^2(x)+\sin^2(x) = 1. \)
Ainsi \( \cos^2(\arcsin(x))+\sin^2(\arcsin(x)) = 1 \; \text{i.e.} \; \cos^2(\arcsin(x)) + x^2 = 1 \; \text{i.e.} \; \displaystyle \cos(\arcsin(x))=\sqrt{1-x^2} \)
D’où \( \forall x \in ]-1,1[, \; \displaystyle f(x) = F^{\prime}(x) = \frac{2}{2\pi\sqrt{x}}\frac{1}{\displaystyle\sqrt{1-x}} = \frac{1}{\pi\sqrt{x(1-x)}} \) une densité de \(X.\)
L’espérance
La démonstration de l’existence de l’espérance ainsi que le calcul pour parvenir à sa valeur est un incontournable, car ce sera l’une des premières questions posées dans un sujet.
Après avoir soigneusement démontré la convergence de l’intégrale, il faut utiliser quelques astuces dans nos calculs :
On a : \( \mathbb{E}(X) = \displaystyle \int_0^1 tf(x) \mathrm{d}t = \int_0^1 (1-u)f(1-u) \mathrm{d}u \) avec le changement de variable \( t = 1 – u. \)
Or \( \forall u \in [0,1], \; f(1-u)=f(u) \; \text{donc} \; \mathbb{E}(X) = \displaystyle \int_0^1 f(u) \mathrm{d}u \; – \int_0^1 uf(u) \mathrm{d}u = 1 – \mathbb{E}(X) \; \text{i.e.} \; 2\mathbb{E}(X)=1 \)
Donc : \( \fbox{\( \mathbb{E}(X) = \displaystyle \frac{1}{2} \) } \)
La variance et la médiane
Contrairement à l’espérance, il n’est généralement pas exigé dans les sujets de savoir retrouver la valeur de la variance et de la médiane, mais il peut être bien de les connaître : \( \fbox{ \( V(X) = \displaystyle \frac{1}{8} \)} \)
De plus, la médiane est ici égale à l’espérance et vaut donc \( \displaystyle \frac{1}{2}. \)
Le lien entre la loi uniforme et la loi arc sinus
Soit \(U\) une variable aléatoire à densité suivant la loi uniforme sur [0,1], alors \( X =\sin^2(\displaystyle \frac{\pi}{2}U) \) suit la loi arc sinus standard.
En effet : \( \forall x \in [0,1], \; P( X \le x) = P(\sin^2(\displaystyle \frac{\pi}{2}U) \le x) = P(\sin(\displaystyle \frac{\pi}{2}U) \le \sqrt{x}) \; \text{car} \; \sin(\displaystyle \frac{\pi}{2}U) \) est à valeurs dans \( \mathbb{R}^+. \)
Donc : \( P( X \le x) = P(\displaystyle \frac{\pi}{2}U \le \arcsin(\sqrt{x})) = P(U \le \displaystyle \frac{2}{\pi} \arcsin(\sqrt{x})) = P( U \le F(x)) = F(x). \) Donc \(X\) suit une loi arc sinus standard.
La loi arc sinus à support borné
Tu t’es peut-être demandé pourquoi la loi que nous venons d’étudier s’appelle la loi arc sinus « standard ». Cela s’explique en étudiant la loi arc sinus à support borné, qui correspond à une généralisation de la loi que nous venons d’aborder.
La loi arc sinus standard peut être étendue à tout support de la forme \( [a,b], \) en considérant la variable aléatoire à densité \(X\) dont la fonction de répartition est : \( \forall x \in [a,b], \; F(x) = \displaystyle{2}{\pi} \arcsin \left( \displaystyle \sqrt{\frac{x-a}{b-a}} \right). \)
Ainsi, la fonction \(f\) telle que \( \forall x \in ]a,b[, \; f(x)= \displaystyle \frac{1}{\sqrt{(x-a)(b-x)}} \) est une densité de \(X.\)
Espérance, variance et médiane
Soit \(X\) une variable aléatoire à densité suivant une loi arc sinus à support borné de paramètres \(a \; \text{et} \; b,\) alors \( \fbox{\( \mathbb{E}(X)= \displaystyle \frac{a + b}{2} \; \text{et} \; V(X)= \frac{1}{8} (b-a)^2\)} \)
De plus, la médiane est ici égale à l’espérance.
La loi arc sinus et la marche aléatoire
Rappelons qu’une marche aléatoire continue généralise le modèle de marche aléatoire discrète, c’est-à-dire des déplacements qui se font par des incréments discrets. Le modèle de marche aléatoire continue permet des déplacements continus. À chaque instant, l’objet peut changer de position de manière continue selon une distribution de probabilité spécifiée.
Il existe un lien entre les marches aléatoires et la loi arc sinus standard qui s’explique à travers l’une des propriétés que nous venons d’étudier. Si l’on considère la variable aléatoire uniforme \(U\) sur \([0,1]\), alors \(=\sin^2(\displaystyle \frac{\pi}{2}U) \) suit la loi arc sinus standard. En effet, \(U\) peut être interprétée comme une représentation des pas aléatoires dans la marche. De plus, la non-linéarité introduite par la fonction sinus dans cette transformation offre un exemple intéressant de la manière dont des concepts simples de probabilité, comme les marches aléatoires, peuvent être liés à des distributions de probabilité plus complexes.
La trigonométrie expliquée dans une vidéo très complète
Si des paroles sont mieux que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette merveilleuse vidéo explicative de Ambroise réalisée sur notre chaîne youtube, il détaille vraiment tout sur tout de la trigonométrie dans les moindres détails…
Aller plus loin
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes nos ressources de trigonométrie sur Major Prépa, que ce soit aussi bien en termes de notions de cours comme de notions hors programme :
| Contenu de trigonométrie au programme et hors programme ECG | |
| Trigo au programme | Trigo hors programme |
| Tout sur les fonctions de trigonométrie cos et sin | Les fonctions de trigonométrie cosh et sinh (cosinus hyperbolique et sinus hyperbolique) |
| Fiche récapitulative des formules de trigo | Trigonométrie et nombres complexes |
| Démonstrations des formules trigonométriques | La loi arcsinus standard et à support borné |
| Zoom sur la fonction Arctangente (Arctan et toutes ses méthodes associées) | Les intégrales de Wallis |
| Vidéo explicative de la trigonométrie | L’intégrale de Dirichelet |
| La trigonométrie (du point de vue du lycée, trigo troisième, trigonométrie en seconde…) | Transformée de Fourier (mais il y a des nombres complexes…) |
| Tout comprendre sur le cercle trigonométrique | |
Conclusion
La loi arc sinus émerge comme une distribution de probabilité particulièrement importante. Son lien avec la loi uniforme et sa généralisation à des supports bornés soulignent à quel point cette notion est vaste, ce qui la rend intéressante pour un sujet de Maths II. À travers l’étude de ses propriétés fondamentales, de la densité à l’espérance, cet article te permet de connaître et de démontrer toutes les propriétés de la loi arc sinus standard ainsi que celles de sa généralisation. Cette diversité de propriétés met en lumière le rôle significatif de cette loi dans les épreuves mathématiques écrites et orales.
Pour maîtriser cette loi de probabilité, tu peux faire le sujet de concours Maths II 2023 (mathématiques approfondies) qui aborde la loi arc sinus standard et qui te fait redémontrer toutes les propriétés que tu viens d’apprendre.
Tu peux retrouver ici toutes nos autres ressources mathématiques !