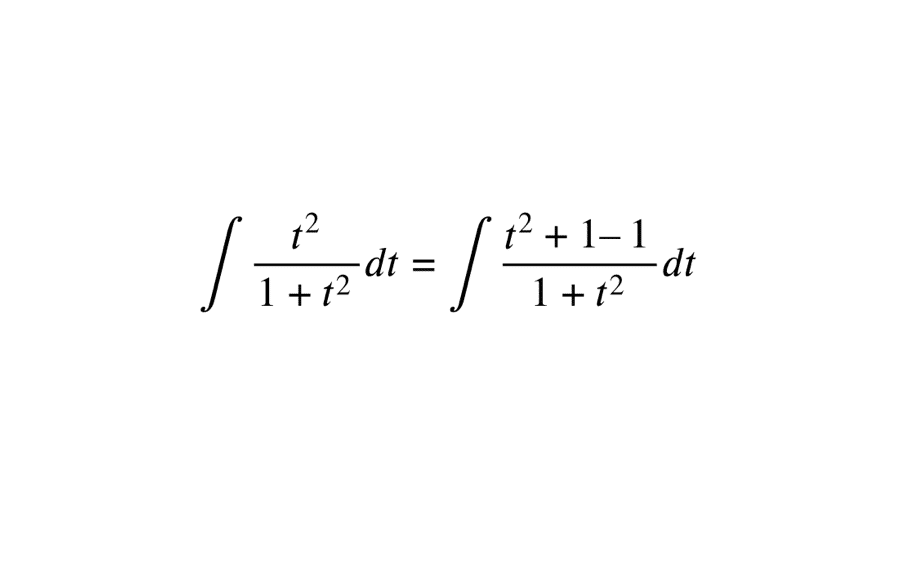L’intégration est une compétence fondamentale en mathématiques, essentielle non seulement pour préparer toutes les épreuves écrites, mais aussi dans de nombreux autres domaines tels que la physique, l’ingénierie et, bien sûr, l’économie elle-même. Cet article vise à dévoiler neuf astuces cruciales pour maîtriser les intégrales, en mettant l’accent sur des calculs détaillés et des techniques efficaces pour simplifier tes efforts d’intégration.
La technique du « +1 -1 »
Considérons l’intégrale \(\displaystyle \int \frac{t^2}{1+t^2} dt\). À première vue, cette intégrale peut sembler complexe. Cependant, en utilisant la technique du « +1 -1 », nous pouvons la simplifier :
\[
\int \frac{t^2}{1+t^2} dt = \int \frac{t^2 + 1 – 1}{1+t^2} dt = \int \frac{t^2 + 1}{1+t^2} dt – \int \frac{1}{1+t^2} dt
\]
Le premier terme est simplement \(\displaystyle \int 1 dt = t\), et le second terme est une intégrale bien connue, \(\displaystyle \int \frac{1}{1+t^2} dt = \arctan(t)\).
Ainsi, l’intégrale initiale devient \(t – \arctan(t) + C\), où \(C\) est la constante d’intégration.
L’intégration de fonctions trigonométriques
L’intégration de produits de fonctions trigonométriques peut parfois paraître délicate, mais avec les bonnes techniques, elle devient bien plus abordable.
Prenons l’exemple de l’intégrale \(\displaystyle \int_0^1 \cos(t)\sin(t) dt\) pour illustrer une méthode efficace. Une approche courante consiste à utiliser les identités trigonométriques pour simplifier l’expression avant d’intégrer.
Dans ce cas, nous pouvons utiliser l’identité trigonométrique \( \displaystyle \sin(2t) = 2\sin(t)\cos(t)\) pour transformer l’intégrale initiale. Cela donne :
\[
\int_0^1 \cos(t)\sin(t) dt = \frac{1}{2}\int_0^1 \sin(2t) dt
\]
Cette simplification transforme le produit de deux fonctions trigonométriques en une seule fonction, rendant l’intégration directe. L’intégrale de \(\sin(2t)\) est plus facile à calculer :
\[
\frac{1}{2}\int_0^1 \sin(2t) dt = -\frac{1}{4}(\cos(2) – \cos(0))
\]
Étant donné que \(\cos(0) = 1\), le résultat final de notre intégrale est \(\displaystyle -\frac{1}{4}(\cos(2) – 1)\). Cette méthode montre comment l’utilisation d’identités trigonométriques pour réécrire les intégrales de produits de fonctions trigonométriques peut simplifier considérablement le processus d’intégration.
Le changement de variable
Le changement de variable est une stratégie d’intégration essentielle, particulièrement efficace pour les intégrales contenant des racines carrées. Un exemple illustratif est l’intégrale \(\displaystyle \int_0^1 \sqrt{1-t^2} dt\), qui apparaît fréquemment dans les problèmes impliquant des géométries circulaires ou des fonctions trigonométriques. Pour aborder cette intégrale, un changement de variable judicieux est nécessaire.
En choisissant le changement de variable \(\displaystyle t = \sin(\theta)\), où \(\displaystyle 0 \leq \theta \leq \frac{\pi}{2}\) pour couvrir l’intervalle de \(0\) à \(1\) dans les termes de \(t\), nous exploitons l’identité trigonométrique fondamentale \(\displaystyle 1 – \sin^2(\theta) = \cos^2(\theta)\) pour simplifier le radical. Avec cette substitution, \(dt = \cos(\theta) d\theta\), transformant l’intégrale originale en :
\[
\int_0^{\frac{\pi}{2}} \cos^2(\theta) d\theta
\]
Cette nouvelle intégrale est plus accessible grâce à l’utilisation des identités trigonométriques, telles que la formule de puissance réduite, \(\displaystyle \cos^2(\theta) = \frac{1 + \cos(2\theta)}{2}\), qui simplifie davantage l’intégration :
\[
\frac{1}{2} \int_0^{\frac{\pi}{2}} (1 + \cos(2\theta)) d\theta
\]
Cette intégrale se résout plus facilement pour finalement donner \(\displaystyle \frac{\pi}{4}\).
L’interprétation géométrique
Rappelons que l’intégrale d’une fonction positive correspond à l’aire entre l’axe des abscisses et la représentation graphique de la fonction. Ainsi, dans certains cas, il peut être intéressant d’étudier directement cette aire.
Reprenons l’exemple précédent, \(\displaystyle \int_0^1 \sqrt{1-t^2} dt\). Ici, l’aire correspond à la surface d’un quart de cercle unitaire, c’est-à-dire \( \displaystyle \frac{\pi}{4}. \) Ce résultat offre une compréhension plus profonde des relations entre les formes géométriques et leurs propriétés algébriques.
L’intégration par parties
L’intégration par parties est une méthode qui découle directement de la formule de dérivation du produit de deux fonctions. Elle est donnée par \(\displaystyle \int_{a}^{b} u v’ dx = \left[ u v \right]_{a}^{b} – \int_{a}^{b} u’ v dx\). Cette technique est particulièrement utile pour intégrer le produit de deux fonctions lorsque l’intégrale directe est complexe ou inconnue.
Prenons l’exemple de l’intégrale \(\displaystyle \int_{0}^{1} t\cos(t) dt\). Pour l’appliquer, nous choisissons \(u = t\) et \(v^{\prime} = \cos(t) \).
En substituant dans la formule d’intégration par parties, nous obtenons : \( \displaystyle \int_{0}^{1} t\cos(t) dt = \left[ t\sin(t) \right]_{0}^{1} – \int_{0}^{1} \sin(t) dt \)
Le calcul de ces intégrales donne : \( \displaystyle \left[ t\sin(t) \right]_{0}^{1} = \sin(1) – 0 = \sin(1) \) et \(
– \int_{0}^{1} \sin(t) dt = \left[ \cos(t) \right]_{0}^{1} = \cos(1) – \cos(0) = \cos(1) – 1 \)
En combinant ces résultats, l’intégrale initiale devient \(\sin(1) + \cos(1) – 1 \).
Cette approche démontre comment l’intégration par parties transforme une intégrale initialement complexe en une somme de termes plus simples à calculer, facilitant ainsi la résolution d’intégrales impliquant des produits de fonctions.
Fractionner les fractions complexes
Considérons \(\displaystyle \int \frac{1}{x^2 – 1} dx\). Cette intégrale peut être simplifiée en utilisant la décomposition en fractions partielles :
\[
\frac{1}{x^2 – 1} = \frac{1}{2(x-1)} – \frac{1}{2(x+1)}
\]
L’intégration donne alors \( \displaystyle \frac{1}{2} \ln |x-1| – \frac{1}{2} \ln |x+1| + C\) où \(C\) est la constante d’intégration.
L’utilisation des symétries
Si une fonction est paire, c’est-à-dire \(f(-x) = f(x)\), alors \( \displaystyle \int_{-a}^{a} f(x) dx = 2\int_{0}^{a} f(x) dx\). Cette propriété peut considérablement simplifier les calculs.
Remarque : Si \(f\) est une fonction impaire, c’est-à-dire \(f(-x) = -f(x)\), alors \( \displaystyle \int_{-a}^{a} f(x) dx = 0 \) avec \(a\) un réel.
L’intégration par parties itérée
L’intégration par parties itérée est une stratégie avancée pour décomposer des intégrales complexes. Cette technique étend le principe de l’intégration par parties standard en appliquant successivement la même formule à l’intégrale résultante de l’application précédente. En répétant ce processus, d’où l’adjectif « itérée », il est possible de décomposer progressivement des intégrales compliquées en des formes plus simples et plus gérables, facilitant ainsi leur résolution.
Soient \( f : [a,b] \to \mathbb{R}\) et \( g : [a,b] \to \mathbb{R}\), deux fonctions de classe \( C^n \) avec \(a < b\) deux réels et \( n \in \mathbb{N}^* \). Alors :
\[ \displaystyle\int_a^bf^{(n)}(t)g(t) \, \mathrm{d}t = \sum_{k=0}^{n-1}(-1)^k \left [ f^{(n-k-1)}(t)g^{(k)}(t)\right]_a^b + (-1)^n\int_a^bf(t)g^{(n)}(t) \, \mathrm{d}t \]
L’astuce de l’intégrale de Riemann
Une astuce fondamentale pour maîtriser les intégrales concerne la compréhension de l’intégrale de Riemann, qui est au cœur du concept d’intégration. L’intégrale de Riemann formalise l’idée d’accumuler des quantités infiniment petites pour calculer l’aire sous une courbe. La formule de base de l’intégrale de Riemann est donnée par :
\[
\int_a^b f(x) dx = \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i^*) \Delta x
\]
Où \([a, b]\) est l’intervalle d’intégration, \(n\) est le nombre de subdivisions de cet intervalle, \(x_i^*\) est un point quelconque dans la \(i\)-ème subdivision, et \( \displaystyle \Delta x = \frac{b-a}{n}\) est la largeur de chaque subdivision.
Conclusion
L’intégration est un outil puissant en mathématiques, et maîtriser ses techniques peut grandement faciliter la résolution de problèmes complexes. En utilisant ces neuf astuces, tu seras mieux équipé(e) pour aborder les intégrales lors des écrits et aux oraux. La pratique régulière et l’application de ces techniques dans différents contextes t’aideront à devenir plus agile et précis(e) dans tes calculs d’intégrales.
Pour t’entraîner sur des calculs d’intégrales, tu peux réaliser les sujets suivants :
- Maths I 2023 (mathématiques approfondies)
- Maths II 1995 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !