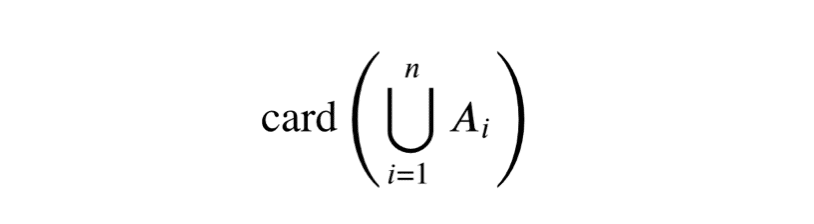La formule du crible de Poincaré est un outil puissant en combinatoire, un domaine des mathématiques qui étudie les arrangements possibles dans des ensembles finis. Elle est particulièrement utile pour déterminer le nombre d’éléments dans l’union de plusieurs ensembles, en tenant compte de leurs intersections multiples. Cet article vise à décomposer et à expliquer la formule itérée du crible de Poincaré et à démontrer son application pratique dans le calcul du nombre de dérangements. Bien que cette notion soit hors programme, il est particulièrement important pour les élèves qui préparent les épreuves parisiennes de la maîtriser.
Théorème de la formule du crible de Poincaré
Le théorème peut être énoncé comme suit : Soit \( E \) un ensemble fini et \( (A_i)_{1 \leq i \leq n} \) une famille de parties de \( E \).
Le cardinal de l’union de ces ensembles est donné par :
\[
\text{card} \left( \bigcup_{i=1}^{n} A_i \right) = \sum_{i=1}^{n} \text{card}(A_i) – \sum_{1 \leq i_1 < i_2 \leq n} \text{card}(A_{i_1} \cap A_{i_2}) + \sum_{1 \leq i_1 < i_2 < i_3 \leq n} \text{card}(A_{i_1} \cap A_{i_2} \cap A_{i_3}) + \cdots + (-1)^{n+1} \text{card}(A_1 \cap \cdots \cap A_n).
\]
La formule est une application du principe d’inclusion-exclusion. Chaque terme corrige les comptes précédents, soit en ajoutant, soit en soustrayant les cardinalités des intersections multiples pour garantir que chaque élément de l’union soit compté exactement une fois.
Application de la formule aux calculs du nombre de dérangements
Un dérangement d’un ensemble fini \( E \) est une permutation sans point fixe, c’est-à-dire une bijection de \( E \) dans lui-même telle que chaque élément est placé dans une position différente de sa position initiale. Pour un ensemble \( E = \{1, …, n\} \), le nombre de dérangements est symbolisé par \( D_n \). La question est : combien y a-t-il de telles permutations, c’est-à-dire de dérangements de \( E \) ?
Soit \( A_i \) l’ensemble des permutations qui laissent l’élément \( i \) dans sa position originale. Le nombre de dérangements est donc le complément du nombre d’arrangements où au moins un élément est fixe :
\[ \text{card}(\overline{A}_1 \cap … \cap \overline{A}_n) = n! – \text{card}(A_1 \cup … \cup A_n) \]
Application de la formule du crible de Poincaré
Pour calculer \( \text{card}(A_1 \cup … \cup A_n) \), nous utilisons la formule du crible de Poincaré : \( \displaystyle \text{card}(A_1 \cup … \cup A_n) = \sum_{k=1}^{n} (-1)^{k-1} S_k. \)
Où \( S_k \) est le nombre de façons de fixer \( k \) éléments parmi \( n \), et se calcule comme : \( \displaystyle S_k = \sum_{1 \leq i_1 < … < i_k \leq n} \text{card}(A_{i_1} \cap … \cap A_{i_k}). \)
Chaque ensemble \( A_{i_1} \cap … \cap A_{i_k} \) correspond aux permutations qui fixent un ensemble spécifique de \( k \) éléments, et donc, le nombre de telles permutations est \( (n-k)! \), le nombre de façons d’arranger les \( n-k \) éléments restants.
En combinant ces informations, nous avons :
\[ S_k = {{n}\choose{k}}(n-k)! = \frac{n!}{k!} \]
Calcul du nombre de dérangements
Le nombre total de dérangements \( D_n \) peut être obtenu en soustrayant le nombre de permutations avec au moins un point fixe du nombre total de permutations de \( E \), soit \( n! \). La formule du crible fournit le nombre de permutations avec des points fixes : \( D_n = n! – \text{card}(A_1 \cup … \cup A_n) \)
En utilisant la formule du crible de Poincaré, nous avons : \( \displaystyle D_n = n! – \sum_{k=1}^{n} (-1)^{k-1} S_k \)
En substituant \( S_k \) par sa valeur, nous obtenons : \( \displaystyle D_n = n! – \sum_{k=1}^{n} (-1)^{k-1} \frac{n!}{k!} \)
Enfin, pour inclure le terme où aucun élément n’est fixe (qui est le dérangement lui-même), on ajoute \( (-1)^n \frac{n!}{n!} \), ce qui donne la formule des dérangements :
\[ D_n = n! \left( \sum_{k=0}^{n} \frac{(-1)^k}{k!} \right) \]
Cette expression représente le nombre de façons de permuter \( n \) éléments sans aucun élément dans sa position initiale. Les termes successifs \( \displaystyle \frac{(-1)^k}{k!} \) ajoutent ou soustraient les permutations avec un nombre croissant de points fixes, assurant que chaque élément est comptabilisé correctement.
La version probabiliste de la formule du crible de Poincaré
La version probabiliste de la formule du crible de Poincaré, aussi connue sous le nom de principe d’inclusion-exclusion en probabilité, permet de déterminer la probabilité de l’union d’événements, qu’il s’agisse de deux événements ou de plusieurs.
Entre deux événements
Considérons deux événements \( A \) et \( B \) issus d’un espace probabilisé. La probabilité que \( A \) ou \( B \) (ou les deux) se produisent est donnée par la somme des probabilités de chaque événement moins la probabilité de leur intersection, pour éviter de compter deux fois les cas où \( A \) et \( B \) se produisent simultanément. La formule est la suivante :
\[ P(A \cup B) = P(A) + P(B) – P(A \cap B) \]
Cette formule est la base de la version probabiliste de la formule du crible et peut être visualisée à l’aide d’un diagramme de Venn. Elle montre que pour deux événements, le calcul des probabilités combine l’addition et la soustraction pour corriger le chevauchement.
Entre n événements
Lorsqu’il y a plus de deux événements, le principe d’inclusion-exclusion devient plus complexe, mais suit la même logique. Pour \( n \) événements \( A_1, A_2, \ldots, A_n \), la probabilité qu’au moins un des événements se produise est donnée par une série alternant des sommes et des soustractions des probabilités des intersections de ces événements :
\[
P\left(\bigcup_{i=1}^{n} A_i\right) = \sum_{i=1}^{n} P(A_i) – \sum_{1 \leq i < j \leq n} P(A_i \cap A_j) + \sum_{1 \leq i < j < k \leq n} P(A_i \cap A_j \cap A_k) – \ldots + (-1)^{n+1}P(A_1 \cap A_2 \cap \ldots \cap A_n)
\]
Cette expression commence par additionner les probabilités de chaque événement individuellement, puis soustrait les probabilités des intersections de chaque paire d’événements pour corriger le double comptage, puis ajoute les probabilités de l’intersection de trois événements, et ainsi de suite. Le signe alterne avec chaque étape supplémentaire de l’intersection, reflétant la correction des surcomptages précédents.
Conclusion
La formule du crible de Poincaré itérée est un outil mathématique d’une grande utilité en dénombrement et en probabilité. Bien qu’elle puisse sembler complexe au premier abord, une compréhension approfondie et une application méthodique révèlent sa capacité à simplifier et à résoudre des problèmes de comptage complexes.
Pour les étudiants préparant les épreuves parisiennes, maîtriser cette formule ouvre la porte à une compréhension plus profonde des probabilités et de la combinatoire, et offre des compétences essentielles pour la réussite de ces épreuves. Pour t’entraîner sur cette notion, tu peux réaliser les sujets ci-dessous qui te feront utiliser la formule du crible :
- Maths II 2014 (mathématiques approfondies)
- Ecricome 2010 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !