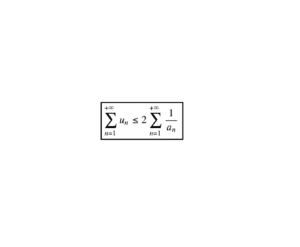Tu vas enfin pouvoir découvrir l’analyse des maths ESCP ECT 2024 ! L’épreuve est très difficile par rapport aux autres épreuves de maths en ECT, mais il est tout de même possible d’avoir une très bonne note ! En effet, il n’est pas nécessaire de finir le sujet pour avoir 20 (comme dans la plupart des épreuves de maths !). Retrouve dans cet article l’analyse du sujet de maths ESCP 2024 pour les ECT ! Retrouvez toutes les informations sur le concours BCE dans notre rubrique Inside Concours BCE 2024 ! Rejoins nous en live tous les soirs de concours dans notre live inside concours BCE pour un débrief rapide de l’épreuve. Tu peux consulter les coefficients détaillés de cette épreuve et voir pour quelles écoles elle compte !
Analyse du sujet des maths ESCP ECT 2024
L’épreuve de maths ESCP compte pour 11 écoles, avec un coefficient qui varie de 4 à 6. C’est un sujet particulièrement attendu.
Commentaires généraux sur le sujet
Cette épreuve présente des notions classiques sous des formes inhabituelles. L’ordre d’apparition des thèmes change également, avec une place importante pour les probabilités et les variables aléatoires. Originalité donc, avec, dès le premier exercice, une densité qui n’est pas nulle là où elle l’est habituellement, et dans le dernier exercice, des suites à traiter de façon différente. Pour t’aider à te positionner, à t’entraîner ou pour te rassurer, voici les principaux points que Major-Prépa a relevés.
Exercice 1
Là où l’on attend habituellement un exercice sur les matrices, c’est une loi exponentielle revisitée qui est présentée. C’est ainsi nouveau d’imaginer cette densité nulle pour \( x\) positif. L’exercice s’appuie sur une bonne connaissance du cours, les questions sont emboîtées, jusqu’à la toute dernière, qui revient sur la toute première question.
Exercice 2
Les matrices, enfin!, avec un exercice relativement classique : l’étude d’une matrice diagonalisable. Si la recherche de vecteurs propres peut te poser quelques problèmes, avec la résolution de \( AX =6X\), les données des questions suivantes te permettent de vérifier tes calculs. On trouve aussi deux inversions de matrices, la première à l’aide de la relation entre \( A, A^2\) et \(I\), la deuxième avec une matrice suggérée, puisque le calcul proposé, qui donne \( PQ = 4I\), permet de déduire que \( P^{-1} = \frac14 Q\). La récurrence demandée en 3.(c) fait partie des récurrences attendues. En application des calculs, un problème avec des chaînes de Markov est proposé. On retrouve le lien habituel entre \( X_{n+1}\), \(A\) et \( X_{n}\), puis l’utilisation de \(A^n\) et des coefficients de la matrice \(X_n\) pour obtenir l’expression de \( d_n\), avant de terminer sur la limite de cette suite. Un grand classique.
Exercice 3
Il s’agit d’un “jeu”, avec deux versions que l’on va comparer, pour savoir quelle est celle qui donne le plus de points. On ne pourra finalement pas les départager. La première version permet de travailler sur la loi Uniforme sur \(([\![1,n]\!]) \) pour \( X\) et la loi de Bernoulli de paramètre \( \frac12 \) pour \( Y\) ; ces deux variables sont alors indépendantes. Dans cette partie sont aussi placées les premières questions Python : un script à compléter et une interprétation à donner. Dans la deuxième et dernière version, les variables ne sont plus indépendantes. La formule des probabilités totales permet de retrouver les mêmes lois pour \( X\) et \( Y\) : le résultat du jeu n’est pas modifié, le nombre moyen de points reste paradoxalement identique.
Exercice 4
Les surprises arrivent avec ce tout dernier exercice, qui t’a mis beaucoup d’étoiles et de petit \( n\) devant les yeux! La première question, avec sa longue relation de récurrence, ses premières hypothèses et son petit calcul tiré de la voie générale (question 1.(c)), cette première question te rappelle vite que c’est bien le sujet ESCP que tu es en train de traiter. Les question suivantes, bien que techniques, se rapprochent de questions plus classiques. Petite remarque : pour la 4.(b), il est préférable de passer par le rapport \( \frac{w_{n+1}}{w_n}\) pour montrer que la suite \( (w_n)\) est constante, ce qui n’est pas habituel. C’est aussi dans ces dernières questions que se trouvent les derniers calculs de dérivation. Des dernières questions qui associent les sommes, avant les séries et les intégrales impropres. En bref, c’est un sujet qui sait présenter des thèmes classiques par des voies originales : un futur “grand classique” ?
Retrouve le sujet de maths ECT ESCP 2024 ici.
Retrouve toutes nos ressources mathématiques.