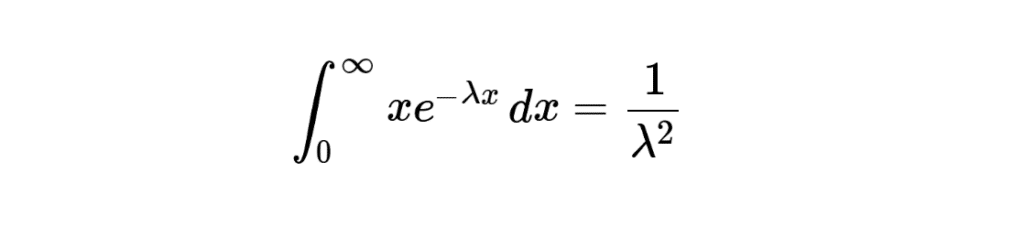Les lois de probabilité sont des outils essentiels en mathématiques, statistiques et probabilités. Elles permettent de modéliser des phénomènes aléatoires et de calculer des probabilités et des espérances. Dans cet article, nous allons explorer quelques astuces pour travailler avec les lois usuelles en faisant des liens entre elles et en utilisant certaines de leurs propriétés pour simplifier des calculs.
1. Le lien entre la loi uniforme et la loi exponentielle
La loi uniforme continue \( U(a, b) \) est une distribution fondamentale en probabilité, où chaque valeur entre \( a \) et \( b \) a une probabilité égale. Cette loi est souvent utilisée comme point de départ pour générer d’autres lois de probabilité. Voici comment la loi exponentielle peut être dérivée de la loi uniforme, en utilisant des transformations appropriées.
Si \( U \) suit une loi uniforme \( U(0, 1) \), alors la variable aléatoire \( -\lambda \ln(U) \) suit une loi exponentielle de paramètre \(\lambda\). En effet, la fonction de répartition \( F(x) \) de la loi exponentielle de paramètre \(\lambda\) est donnée par :
\[ F(x) = 1 – e^{-\lambda x} \]
Pour trouver la variable aléatoire correspondant à cette loi à partir de \( U \), on résout :
\[ U = 1 – e^{-\lambda x} \]
En isolant \( x \), nous obtenons :
\[ x = -\frac{\ln(1-U)}{\lambda} \]
Comme \( 1-U \) suit également une loi uniforme \( U(0, 1) \), nous pouvons simplifier et écrire :
\[ x = -\frac{\ln(U)}{\lambda} \]
Par conséquent, si \( U \sim U(0, 1) \), alors \( X = -\frac{\ln(U)}{\lambda} \) suit une loi exponentielle de paramètre \( \lambda. \)
2. La méthode de Box-Muller
La méthode de Box-Muller est une technique bien connue pour générer des variables aléatoires suivant une loi normale \( N(0, 1) \) à partir de deux variables aléatoires uniformes indépendantes. Supposons \( U_1 \) et \( U_2 \) sont deux variables indépendantes suivant la loi \( U(0, 1) \). La méthode de Box-Muller donne deux variables aléatoires indépendantes \( Z_0 \) et \( Z_1 \) suivant \( N(0, 1) \) par les transformations suivantes :
\[ Z_0 = \sqrt{-2 \ln(U_1)} \cos(2\pi U_2) \]
\[ Z_1 = \sqrt{-2 \ln(U_1)} \sin(2\pi U_2) \]
Ces transformations exploitent les propriétés de la loi uniforme pour générer des variables suivant une loi normale.
3. Utiliser la loi normale pour évaluer des intégrales gaussiennes
Les intégrales impliquant des exponentielles quadratiques, appelées intégrales gaussiennes, apparaissent fréquemment en mathématiques, physique et statistiques. La loi normale est particulièrement utile pour évaluer ces intégrales de manière analytique.
Propriété de la loi normale
La densité de probabilité de la loi normale \( N\left(0, \frac{1}{2}\right) \) est donnée par :
\[ f(x) = \sqrt{\frac{1}{\pi}} e^{-x^2} \]
Nous pouvons utiliser cette propriété pour évaluer des intégrales de la forme :
\[ \int_{-\infty}^{\infty} e^{-x^2} \, dx \]
Exemple pratique
Considérons l’intégrale suivante :
\[ I = \int_{-\infty}^{\infty} e^{-x^2} \, dx \]
Pour évaluer cette intégrale, reconnaissons qu’elle est liée à la densité de probabilité de la loi normale \( N\left(0, \frac{1}{2}\right) \). En fait, la densité de la loi normale \( N\left(0, \frac{1}{2}\right) \) intégrée sur toute la ligne réelle est égale à 1 :
\[ \int_{-\infty}^{\infty} \sqrt{\frac{1}{\pi}} e^{-x^2} \, dx = 1 \]
Nous pouvons sortir le facteur \(\sqrt{\frac{1}{\pi}}\) de l’intégrale et la réécrire comme suit :
\[ \sqrt{\frac{1}{\pi}} \int_{-\infty}^{\infty} e^{-x^2} \, dx = 1 \]
En multipliant les deux côtés par \(\sqrt{\pi}\), nous obtenons :
\[ \int_{-\infty}^{\infty} e^{-x^2} \, dx = \sqrt{\pi} \]
Ce qui montre que l’intégrale de Gauss est :
\[ \int_{-\infty}^{\infty} e^{-x^2} \, dx = \sqrt{\pi} \]
Utiliser la loi normale pour évaluer des intégrales gaussiennes simplifie grandement les calculs et permet d’obtenir des résultats précis et rapides. Cette méthode est particulièrement utile dans les domaines de la physique, de la statistique et de l’analyse mathématique.
4. Calculer des intégrales grâce à l’espérance d’une loi exponentielle
La loi exponentielle est souvent utilisée pour simplifier le calcul des intégrales. Si \( X \) suit une loi exponentielle de paramètre \(\lambda\), alors son espérance est donnée par :
\[ \mathbb{E}[X] = \frac{1}{\lambda} \]
Cette propriété peut être utilisée pour calculer des intégrales. Par exemple, considérons l’intégrale :
\[ \int_{0}^{\infty} x e^{-\lambda x} \, dx \]
En reconnaissant que cette intégrale représente l’espérance de \( X \) sous une loi exponentielle de paramètre \(\lambda\), tu n’as pas plus besoin de réaliser une IPP ce qui te simplifie les calculs, nous obtenons ainsi :
\[ \int_{0}^{\infty} x e^{-\lambda x} \, dx = \frac{1}{\lambda^2} \]
5. Utiliser la loi Gamma pour calculer des intégrales impliquant des puissances
La loi Gamma est particulièrement utile pour évaluer des intégrales impliquant des puissances de variables, en particulier celles qui apparaissent fréquemment en théorie des probabilités et en statistiques.
Propriété de la loi Gamma
Si \( X \) suit une loi Gamma \(\text{Gamma}(\alpha, \beta)\) avec les paramètres \(\alpha\) et \(\beta\), alors sa densité de probabilité est donnée par :
\[ f_X(x) = \frac{\beta^\alpha x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)} \quad \text{pour } x > 0 \]
Cette propriété peut être utilisée pour calculer des intégrales de la forme :
\[ \int_{0}^{\infty} x^{\alpha-1} e^{-\beta x} \, dx \]
Exemple pratique
Considérons l’intégrale suivante :
\[ I = \int_{0}^{\infty} x^3 e^{-2x} \, dx \]
Nous reconnaissons que l’intégrande \( x^3 e^{-2x} \) est liée à la densité de probabilité de la loi Gamma avec \(\alpha = 4\) et \(\beta = 2\). En effet, si \( X \) suit une loi Gamma \(\text{Gamma}(4, 2)\), alors :
\[ f_X(x) = \frac{2^4 x^{4-1} e^{-2x}}{\Gamma(4)} = \frac{16 x^3 e^{-2x}}{6} = \frac{8}{3} x^3 e^{-2x} \]
L’intégrale peut donc être réécrite en termes de la densité de la loi Gamma. Pour trouver \( I \), nous utilisons la propriété de la loi Gamma qui nous dit que :
\[ \int_{0}^{\infty} x^{\alpha-1} e^{-\beta x} \, dx = \frac{\Gamma(\alpha)}{\beta^\alpha} \]
En substituant les valeurs \(\alpha = 4\) et \(\beta = 2\), nous avons :
\[ I = \int_{0}^{\infty} x^3 e^{-2x} \, dx = \frac{\Gamma(4)}{2^4} \]
Nous savons que \(\Gamma(4) = 3! = 6 \)
Ainsi, l’intégrale devient : \( \displaystyle I = \frac{6}{2^4} = \frac{6}{16} = \frac{3}{8} \)
Donc, \( \displaystyle \int_{0}^{\infty} x^3 e^{-2x} \, dx = \frac{3}{8} \)
Utiliser la loi Gamma pour évaluer des intégrales de cette forme simplifie grandement les calculs et permet d’obtenir des résultats précis de manière efficace. Cette méthode est particulièrement utile dans les domaines de la théorie des probabilités, de la statistique et de l’analyse mathématique.
6. Utiliser la loi de Poisson pour approximer la loi binomiale
Lorsque le nombre d’essais \( n \) est grand et que la probabilité de succès \( p \) est petite, la loi de Poisson peut être utilisée pour approximer une loi binomiale. Cette approximation est particulièrement utile pour simplifier les calculs dans les cas où \( n \) est grand et \( p \) est petit.
Formule de l’approximation
Si \( X \) suit une loi binomiale \( B(n, p) \), alors pour \( n \) grand et \( p \) petit tel que \( \lambda = np \) reste constant, \( X \) peut être approximée par une loi de Poisson de paramètre \( \lambda \):
\[ X \sim \text{Poisson}(\lambda) \]
Exemple pratique
Supposons que nous avons un très grand nombre \( n \) de balles (par exemple, \( n = 1000 \)), et que chaque balle a une petite probabilité \( p \) de réussite (par exemple, \( p = 0.002 \)). Le nombre moyen de succès attendu est \( \lambda = np \):
\[ \lambda = 1000 \times 0.002 = 2 \]
Nous voulons calculer la probabilité d’obtenir exactement 3 succès. Utiliser directement la formule de la loi binomiale pour un grand \( n \) serait compliqué, mais nous pouvons utiliser l’approximation de Poisson.
Pour la loi de Poisson de paramètre \( \lambda = 2 \), la probabilité d’obtenir exactement 3 succès est :
\[ P(X = 3) = \frac{2^3 e^{-2}}{3!} \]
Calculons cela étape par étape : \( 2^3 = 8 \; \text{et} \; e^{-2} \approx 0.1353 \; \text{et} \; 3! = 6 \)
Ainsi, \( P(X = 3) = \frac{8 \times 0.1353}{6} \approx 0.1804 \)
Cette approximation montre comment la loi de Poisson peut simplifier les calculs de probabilités dans des situations où la loi binomiale serait autrement complexe à manipuler. En utilisant cette méthode, nous pouvons facilement gérer des problèmes impliquant de grands \( n \) et de petits \( p \), rendant les calculs plus pratiques et accessibles.
Conclusion
Les lois de probabilité, en particulier les lois usuelles telles que les lois uniforme, exponentielle, normale, gamma, et beta, offrent une variété d’outils puissants pour simplifier et résoudre des problèmes complexes en probabilités et en statistiques. En comprenant les relations entre ces lois et en utilisant leurs propriétés uniques, on peut transformer des calculs difficiles en solutions plus gérables. Les astuces présentées dans cet article montrent comment tirer parti de ces propriétés pour dériver des distributions, évaluer des intégrales, et simplifier des expressions.
Pour t’entrainer à utiliser ces astuces tu peux réaliser les sujets suivants :
- Maths II 2023 (mathématiques approfondies)
- Maths EML 2024 (mathématiques approfondies)
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !