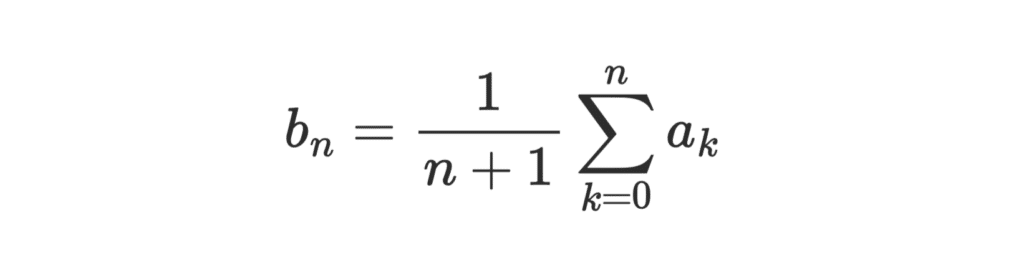Les suites sont un outil fondamental en mathématiques, utilisées pour modéliser et analyser des séquences de nombres. Leur étude permet de comprendre des concepts clés tels que la convergence, la divergence et les comportements asymptotiques. Dans cet article, nous allons explorer quelques astuces avancées mais accessibles pour travailler avec les suites, en mettant en évidence des techniques qui peuvent simplifier les calculs et améliorer la compréhension des séquences.
1. Utiliser le critère des sous-suites (suites extraites) pour démontrer la convergence
Une méthode puissante pour démontrer la convergence d’une suite est d’examiner ses sous-suites (aussi appelées suites extraites). Si toutes les sous-suites convergent vers le même réel, alors la suite entière converge vers ce même réel.
Exemple pratique
Considérons une suite \( (a_n) \) dont nous soupçonnons qu’elle converge vers un réel \( L \). Pour appliquer ce critère, nous devons montrer que toutes les sous-suites de \( (a_n) \) convergent vers \( L \).
1. Identifier des sous-suites :
Supposons que \( (a_{n_k}) \) soit une sous-suite de \( (a_n) \) et que les indices des sous-suites couvrent l’ensemble des entiers naturels \( \mathbb{N} \). Par exemple, les sous-suites des termes pairs \( (a_{2k}) \) et des termes impairs \( (a_{2k+1}) \) partitionnent \( \mathbb{N} \).
2. Montrer que chaque sous-suite converge vers \( L \) :
Par exemple, si nous pouvons démontrer que pour toute sous-suite \( (a_{n_k}) \), nous avons \( \lim \limits_{k \to +\infty} a_{n_k} = L \), alors il en résulte que \( \lim \limits_{n \to +\infty} a_n = L \).
Ce critère est particulièrement utile dans des situations où la suite elle-même peut être compliquée à analyser directement, mais où ses sous-suites sont plus faciles à étudier. En démontrant que toutes les sous-suites convergent vers le même réel, nous pouvons établir la convergence de la suite entière de manière rigoureuse.
2. Utiliser les suites adjacentes pour démontrer la convergence
Les suites adjacentes sont deux suites qui se rapprochent l’une de l’autre et convergent vers la même limite. Cette méthode est souvent utilisée pour démontrer la convergence de suites définies de manière complexe.
Énoncé
Deux suites \((a_n)\) et \((b_n)\) sont dites adjacentes si \((a_n)\) est croissante, \((b_n)\) est décroissante, et \(a_n \leq b_n\) pour tout \(n\). Si \((a_n)\) et \((b_n)\) sont adjacentes et convergent, elles convergent vers la même limite.
Exemple pratique
Considérons les suites \((S_n)\) et \((S’_n)\) définies par :
\[ S_n = \sum_{k=1}^{n} \frac{1}{k^2} \]
\[ S’_n = S_n + \frac{1}{n} \]
Nous voulons montrer que \((S_n)\) et \((S’_n)\) sont adjacentes et convergent vers la même limite.
1. Montrer que \((S_n)\) est croissante et \((S’_n)\) est décroissante :
– Pour \((S_n)\), nous avons \( S_{n+1} = S_n + \frac{1}{(n+1)^2} \). Donc, \( S_{n+1} – S_n = \frac{1}{(n+1)^2} \geq 0 \), ce qui signifie que \((S_n)\) est croissante.
– Pour \((S’_n)\), nous avons \( S’_{n+1} = S_{n+1} + \frac{1}{n+1} = S_n + \frac{1}{(n+1)^2} + \frac{1}{n+1} \). Donc, \( \displaystyle S’_{n+1} – S’_n = \left(S_n + \frac{1}{(n+1)^2} + \frac{1}{n+1}\right) – \left(S_n + \frac{1}{n}\right) = \frac{1}{(n+1)^2} + \frac{1}{n+1} – \frac{1}{n} \)
Or, \( \frac{1}{(n+1)^2} + \frac{1}{n+1} – \frac{1}{n} \leq 0. \) Donc \( S’_{n+1} \leq S’_n \), ce qui signifie que \((S’_n)\) est décroissante.
2. Montrer que \((S_n)\) et \((S’_n)\) sont adjacentes :
Par construction, \( S_n \leq S’_n \) pour tout \( n \), et nous avons montré que \((S_n)\) est croissante et \((S’_n)\) est décroissante. De plus la différence des deux suites converge vers 0. Donc, \((S_n)\) et \((S’_n)\) sont adjacentes.
Étant donné que \((S_n)\) et \((S’_n)\) sont adjacentes, par le théorème des suites adjacentes, elles convergent vers la même limite \( L \).
3. Étudier la convergence des suites géométriques
Une suite géométrique est une suite de nombres où le rapport entre deux termes consécutifs est constant. Si \( v_n \) est le \( n \)-ième terme de la suite, alors : \( v_n = v_0 \cdot q^n \) où \( v_0 \) est le premier terme et \( q \) est la raison de la suite. La raison de cette suite nous permet de conclure quant à la convergence de la suite étudiée.
Exemple pratique
Pour déterminer si une suite géométrique converge, nous examinons la raison \( q \). Si \( |q| < 1 \), alors la suite converge vers 0. Si \( |q| \geq 1 \) et si le premier terme n’est pas nul, la suite diverge.
Considérons une suite géométrique où \( v_0 = 10 \) et \( q = \frac{1}{2} \). Les premiers termes sont 10, 5, 2.5, 1.25, … Puisque \( |q| = \frac{1}{2} < 1 \), cette suite converge vers 0.
4. Utiliser le lemme de Cesaro pour les suites convergentes
Le lemme de Cesaro est une technique puissante en analyse des suites et séries, qui permet de simplifier l’étude de la convergence des suites. Il stipule que si une suite est convergente, alors la suite de ses moyennes arithmétiques est également convergente et converge vers la même limite.
Énoncé du lemme de Cesaro
Si \( (a_n) \) est une suite convergente de limite \( L \), alors la suite des moyennes arithmétiques de \( (a_n) \), définie par :
\[ b_n = \frac{1}{n+1} \sum_{k=0}^{n} a_k \]
converge également vers \( L \).
Exemple pratique
Considérons une suite \( (a_n) \) définie par \( a_n = \frac{1}{n} \). Nous savons que cette suite converge vers 0. Appliquons le lemme de Cesaro pour démontrer que la suite des moyennes arithmétiques de \( a_n \) converge également vers 0.
La suite des moyennes arithmétiques \( (b_n) \) est définie par :
\[ b_n = \frac{1}{n+1} \sum_{k=0}^{n} \frac{1}{k+1} \]
Pour montrer que \( b_n \) converge vers 0, nous utiliserions le lemme de Cesaro. Intuitivement, nous savons que puisque chaque terme \( a_n \) devient de plus en plus petit, la moyenne arithmétique de ces termes tend également vers 0.
Utiliser le lemme de Cesaro est particulièrement utile lorsque tu travailles avec des suites définies par des moyennes ou lorsque tu souhaites démontrer la convergence de suites complexes en les ramenant à l’étude de suites plus simples.
5. Utiliser la méthode des différences finies pour analyser les suites
La méthode des différences finies est une technique utile pour étudier les suites, en particulier pour comprendre leur comportement asymptotique et pour détecter des modèles ou des régularités. Cette méthode consiste à examiner les différences entre termes successifs d’une suite.
La première différence finie d’une suite \( (a_n) \) est définie par :
\[ \Delta a_n = a_{n+1} – a_n \]
De même, la seconde différence finie est définie par :
\[ \Delta^2 a_n = \Delta a_{n+1} – \Delta a_n \]
Exemple pratique
Considérons une suite \( (a_n) \) définie par \( a_n = n^2 \). Nous pouvons utiliser la méthode des différences finies pour analyser cette suite.
1. Calculer la première différence finie :
\[ \Delta a_n = a_{n+1} – a_n = (n+1)^2 – n^2 = n^2 + 2n + 1 – n^2 = 2n + 1 \]
2. Calculer la seconde différence finie :
\[ \Delta^2 a_n = \Delta a_{n+1} – \Delta a_n = (2(n+1) + 1) – (2n + 1) = 2n + 2 + 1 – 2n – 1 = 2 \]
Nous voyons que la seconde différence finie est constante. Ce qui est cohérent avec notre définition initiale d’une forme quadratique.
La méthode des différences finies est particulièrement utile pour :
– Détecter des tendances linéaires, quadratiques, ou plus complexes dans les suites.
– Analyser les suites récurrentes et comprendre leur comportement asymptotique.
– Simplifier des suites complexes en les transformant en suites de différences plus faciles à manipuler.
6. Analyser la convergence des suites définies par une fonction du terme précédent
Les suites définies par une relation de récurrence \( u_{n+1} = f(u_n) \) sont courantes en mathématiques et apparaissent dans divers domaines tels que les équations différentielles et les systèmes dynamiques. Voici les étapes pour analyser leur convergence :
1. Trouver les points fixes de \( f \) :
Un point fixe \( L \) de la fonction \( f \) est une valeur telle que \( f(L) = L \). Pour trouver les points fixes, on résout l’équation : \( f(x) = x. \)
2. Étudier la stabilité des points fixes :
Pour déterminer si un point fixe \( L \) est stable (attractif), on examine la dérivée \( f’ \) au point fixe. Si \( |f'(L)| < 1 \), alors \( L \) est un point fixe attractif et la suite \( (u_n) \) convergera vers \( L \) si elle est initialement proche de \( L \).
3. Analyser le comportement initial :
La convergence de la suite dépend de la valeur initiale \( u_0 \). Si \( u_0 \) est suffisamment proche d’un point fixe attractif, la suite \( (u_n) \) convergera vers ce point fixe.
Utiliser ces techniques permet d’aborder les suites récurrentes avec plus d’efficacité et de déterminer leur comportement asymptotique de manière rigoureuse.
7. Utiliser le théorème de Bolzano-Weierstrass pour les suites
Le théorème de Bolzano-Weierstrass est un résultat fondamental en analyse, qui stipule que toute suite bornée dans \( \mathbb{R} \) possède une sous-suite convergente. Ce théorème est très utile pour démontrer l’existence de limites et comprendre le comportement des suites.
Idée intuitive de la démonstration
1. Suite bornée :
Si une suite \( (a_n) \) est bornée, cela signifie qu’il existe des bornes \( m \) et \( M \) telles que \( m \leq a_n \leq M \) pour tout \( n \).
2. Subdivision de l’intervalle :
On peut subdiviser l’intervalle \([m, M]\) en deux sous-intervalles de longueurs égales. Au moins un de ces sous-intervalles contiendra une infinité de termes de la suite \( (a_n) \) en raison de la nature infinie de la suite.
3. Choix récursif d’intervalles :
En répétant le processus de subdivision sur le sous-intervalle contenant une infinité de termes, on obtient une suite d’intervalles emboîtés dont les longueurs tendent vers zéro.
4. Extraction de la sous-suite :
À chaque étape de subdivision, on choisit un terme de la suite \( (a_n) \) appartenant à l’intervalle contenant une infinité de termes. Cette sélection garantit que la sous-suite ainsi formée est convergente, car les intervalles se resserrent autour d’un point limite.
5. Convergence de la sous-suite :
La sous-suite obtenue converge vers un certain réel \( L \), qui est le point commun à tous les intervalles emboîtés.
8. Utiliser la méthode de Stolz-Cesaro pour les limites de suites
La méthode de Stolz-Cesaro est un outil puissant pour évaluer les limites de suites lorsque la forme de la suite est complexe. Elle est particulièrement utile pour les suites de type quotient.
Théorème de Stolz-Cesaro
Soit \( (a_n) \) et \( (b_n) \) deux suites réelles telles que \( (b_n) \) est strictement croissante et tend vers l’infini. Si \( \lim_{n \to \infty} \frac{a_{n+1} – a_n}{b_{n+1} – b_n} = L \), alors :
\[ \lim_{n \to \infty} \frac{a_n}{b_n} = L \]
Exemple pratique
Considérons la suite \( u_n = \sum_{k=1}^{n} \frac{1}{k} \) et \( v_n = \ln(n) \). Nous voulons trouver la limite de \( \frac{u_n}{v_n} \) lorsque \( n \to \infty \).
Nous appliquons le théorème de Stolz-Cesaro avec \( a_n = \sum_{k=1}^{n} \frac{1}{k} \) et \( b_n = \ln(n) \). Calculons les différences :
\[ a_{n+1} – a_n = \frac{1}{n+1} \]
\[ b_{n+1} – b_n = \ln(n+1) – \ln(n) \sim \frac{1}{n} \]
En utilisant ces différences, nous obtenons :
\[ \lim_{n \to \infty} \frac{a_{n+1} – a_n}{b_{n+1} – b_n} = \lim_{n \to \infty} \frac{\frac{1}{n+1}}{\frac{1}{n}} = \lim_{n \to \infty} \frac{n}{n+1} = 1 \]
Donc, par le théorème de Stolz-Cesaro :
\[ \lim_{n \to \infty} \frac{u_n}{v_n} = 1 \]
Cela montre que :
\[ \lim_{n \to \infty} \frac{\sum_{k=1}^{n} \frac{1}{k}}{\ln(n)} = 1 \]
9. Utiliser les suites de Cauchy pour démontrer la convergence
Les suites de Cauchy sont un concept central en analyse réelle et servent souvent à démontrer la convergence d’une suite sans connaître explicitement sa limite.
Définition
Une suite \( (a_n) \) est une suite de Cauchy si, pour tout \(\epsilon > 0\), il existe un entier \( N \) tel que pour tout \( m, n \geq N \), nous avons :
\[ |a_n – a_m| < \epsilon \]
Exemple pratique
Considérons la suite définie par : \[ a_n = \frac{1}{n} \] Pour démontrer que \( (a_n) \) est une suite de Cauchy, nous montrons que pour tout \(\epsilon > 0\), il existe un entier \( N \) tel que pour tout \( m, n \geq N \), nous avons :
\[ \left| \frac{1}{n} – \frac{1}{m} \right| < \epsilon \]
Puisque \( \frac{1}{n} \to 0 \) et \( \frac{1}{m} \to 0 \) lorsque \( n, m \to \infty \), nous pouvons trouver un \( N \) tel que pour tout \( n, m \geq N \), les termes de la suite sont arbitrairement proches de zéro. En fait, nous pouvons choisir \( N \) tel que :
\[ \frac{1}{N} < \epsilon \]
Ainsi, pour tout \( m, n \geq N \), nous avons :
\[ \left| \frac{1}{n} – \frac{1}{m} \right| \leq \left| \frac{1}{n} \right| + \left| \frac{1}{m} \right| < \epsilon \]
Donc, \( (a_n) \) est une suite de Cauchy et par conséquent, elle converge.
Conclusion
Les suites, en tant qu’outil fondamental en mathématiques, offrent de nombreuses possibilités d’analyse et de compréhension des comportements des séquences de nombres. Grâce aux astuces présentées dans cet article, tu as pu explorer différentes méthodes pour analyser et démontrer la convergence des suites.
Pour t’entrainer à utiliser ces astuces tu peux réaliser les sujets suivants :
- Maths EDHEC 2017 (mathématiques approfondies)
- Maths EML 2021 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !