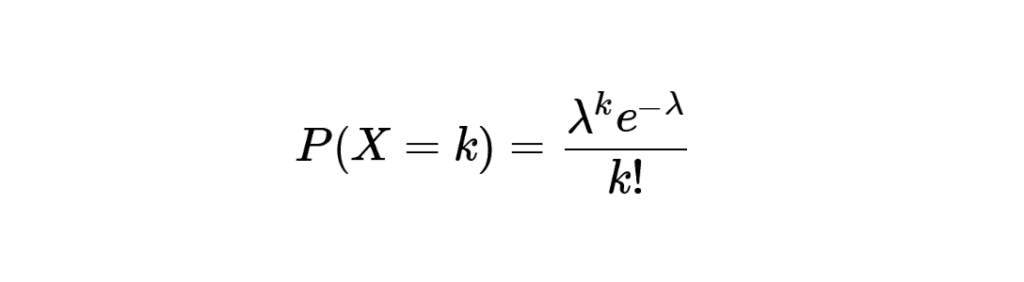La loi de Poisson est une distribution de probabilités discrète qui exprime la probabilité qu’un certain nombre d’événements se produisent dans un intervalle de temps fixe, lorsque ces événements se produisent avec une moyenne connue et indépendamment du temps écoulé depuis l’événement précédent. Dans cette article tu découvriras plusieurs notions hors programme liées à cette distribution qui te permettront de te préparer au mieux aux épreuves parisiennes et aux oraux de mathématiques.
Situtation Concrète
De nombreuses situations de la vie courante peuvent être modélisées par une loi de Poisson. Par exemple, le nombre de clients arrivant à un guichet de banque en une heure, le nombre de pannes d’un réseau informatique en une année, ou le nombre de malades arrivant aux urgences d’un hôpital en une nuit. Ces phénomènes sont appelés des phénomènes d’attente. Pour décrire ces événements, on peut soit chercher le nombre de réalisations de l’événement dans un intervalle de temps donné (ce qui suit une loi de Poisson), soit chercher le temps entre deux réalisations successives de l’événement (ce qui suit une loi exponentielle).
La Distribution de Poisson
La distribution de Poisson est définie par la formule suivante :
\[ P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \]
où \( \lambda \) est le nombre moyen d’événements se produisant dans un intervalle de temps donné, \( k \) est le nombre d’événements.
Propriétés de la Loi de Poisson
Quelques propriétés importantes de la distribution de Poisson incluent :
Moyenne et Variance : La moyenne et la variance sont toutes deux égales à \( \lambda \).
Additivité : Si \( X_1 \) et \( X_2 \) sont deux variables aléatoires indépendantes suivant des lois de Poisson de paramètres \( \lambda_1 \) et \( \lambda_2 \), alors \( X_1 + X_2 \) suit une loi de Poisson de paramètre \( \lambda_1 + \lambda_2 \). Cela peut donc se généraliser pour une somme de \(n\) variables aléatoires
Moment Généralisé : Le \( k \)-ième moment d’une distribution de Poisson peut être calculé en utilisant la formule des moments. Pour une variable \( X \) suivant une loi de Poisson de paramètre \( \lambda \), le \( k \)-ième moment est donné par :
\[ \mathbb{E}(X^k) = \sum_{i=0}^{\infty} i^k \frac{\lambda^i e^{-\lambda}}{i!} \]
Bien que cette formule puisse être complexe à calculer directement pour des valeurs élevées de \( k \), elle démontre l’intérêt théorique des moments dans l’étude de la distribution.
Modes de la Distribution Poissonienne
Le mode d’une distribution de Poisson est la valeur de \( k \) qui maximise la probabilité \( P(X = k) \). Pour déterminer le mode, nous devons trouver le \( k \) qui maximise la fonction de probabilité :
\[ P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \]
Pour ce faire, nous considérons le ratio des probabilités consécutives :
\[ \frac{P(X = k+1)}{P(X = k)} = \frac{\frac{\lambda^{k+1} e^{-\lambda}}{(k+1)!}}{\frac{\lambda^k e^{-\lambda}}{k!}} = \frac{\lambda^{k+1}}{(k+1)!} \cdot \frac{k!}{\lambda^k} = \frac{\lambda}{k+1} \]
Nous trouvons le \( k \) pour lequel ce ratio est inférieur ou égal à 1, c’est-à-dire :
\[ \frac{\lambda}{k+1} \leq 1 \]
Ce qui implique :
\[ \lambda \leq k+1 \]
Ainsi, \( k \geq \lambda – 1 \). Étant donné que \( k \) doit être un entier, nous avons :
\[ k = \lfloor \lambda \rfloor \text{ ou } k = \lfloor \lambda \rfloor + 1 \]
où \( \lfloor \cdot \rfloor \) représente la fonction partie entière. Autrement dit, le mode est la partie entière de \( \lambda \) ou la partie entière de \( \lambda \) plus un.
En résumé, pour une loi de Poisson de paramètre \( \lambda \), le mode est une valeur critique qui maximise la probabilité de la distribution, et peut être déterminée analytiquement en étudiant les ratios de probabilités consécutives. Cela nous permet de comprendre et de prédire les valeurs les plus probables dans un ensemble de données modélisées par une distribution de Poisson.
Approximation de la Loi Binomiale
La loi de Poisson peut être interprétée comme un cas limite de la loi binomiale. Lorsque le nombre d’essais \( n \) est très grand et que la probabilité de succès \( p \) est très petite, tout en gardant le produit \( np \) constant, la loi binomiale \( B(n, p) \) peut être approximée par une loi de Poisson de paramètre \( \lambda = np \).
Preuve. Si \( Y \) suit une loi \( B(n, \lambda/n) \), on sait que :
\[ P(Y = k) = {{n}\choose{k}} \left( \frac{\lambda}{n} \right)^k \left(1 – \frac{\lambda}{n} \right)^{n-k} \]
Cette équation peut être réécrite comme suit :
\[ = (1 – \frac{\lambda}{n})^{n-k} \frac{\lambda^k}{k!} \frac{n(n-1) \cdots (n-k+1)}{n^k} \]
Ensuite, on peut simplifier l’expression :
\[ = (1 – \frac{\lambda}{n})^n \frac{\lambda^k}{k!} (1 – \frac{\lambda}{n})^{-k} \left[ \frac{n}{n} \times \frac{n-1}{n} \times \cdots \times \frac{n-k+1}{n} \right] \]
Chaque terme du produit entre crochets tend vers 1 lorsque \( n \) tend vers l’infini. Il y a \( k \) termes, c’est-à-dire un nombre fini, donc le crochet tend vers 1. De même, \( (1 – \frac{\lambda}{n})^{-k} \) tend vers 1. De plus,
\[ \ln((1 – \frac{\lambda}{n})^n) = n \ln(1 – \frac{\lambda}{n}) \sim n \times (-\frac{\lambda}{n}) \]
Cette simplification nous montre que l’expression tend vers \( -\lambda \) lorsque \( n \) tend vers l’infini. Par conséquent, \( \displaystyle (1 – \frac{\lambda}{n})^n \) tend vers \( e^{-\lambda} \). Ainsi, en combinant toutes ces observations, on conclut que \( P(Y = k) \) tend vers \( e^{-\lambda} \frac{\lambda^k}{k!} \).
Cela montre clairement comment la loi binomiale, sous certaines conditions, converge vers une loi de Poisson. Cette approximation est particulièrement utile dans des situations où \( n \) est grand et \( p \) est petit, comme dans les exemples de phénomènes d’attente mentionnés précédemment. Cette démonstration est fondamentale pour comprendre les liens entre ces deux distributions et leur utilisation pratique en statistiques et en probabilité.
Diagramme de la Distribution Poissonienne
Un diagramme de distribution de Poisson est souvent représenté sous la forme d’un histogramme où l’axe des abscisses représente le nombre d’événements \( k \) et l’axe des ordonnées représente la probabilité \( P(X = k) \). La forme du diagramme dépend du paramètre \( \lambda \). Pour de petites valeurs de \( \lambda \), la distribution est fortement asymétrique avec une queue longue à droite. À mesure que \( \lambda \) augmente, la distribution devient plus symétrique et se rapproche d’une distribution normale.
Conclusion des modes de distribution poissonnienne
La loi de Poisson est un outil puissant et flexible pour modéliser des événements discrets se produisant dans un intervalle de temps. Sa capacité à approximer la loi binomiale dans certains cas en fait une distribution essentielle en statistiques et en probabilité. En comprenant ses propriétés, sa forme et ses modes, tu pourras mieux appréhender les phénomènes d’attente et appliquer ces concepts à des situations concrètes.
Pour t’entrainer sur cette notion tu peux réaliser les sujets suivants :
- Ecricome 2018 (mathématiques approfondies)
- EML 2018 (mathématiques approfondies)
- EDHEC 2013 (mathématiques approfondies)
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !