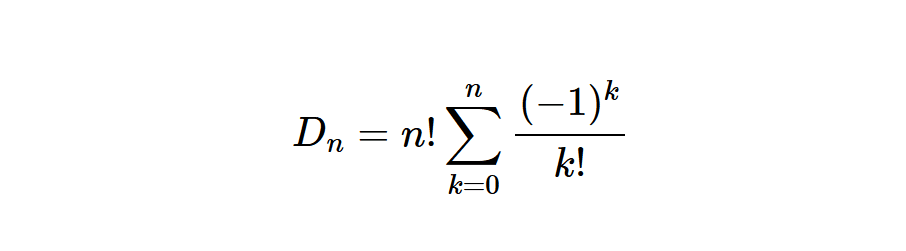Dans chaque sujet de Parisienne, il n’est pas rare de retrouver des notions hors programme. Puisque Maths II s’oriente plutôt vers les probabilités, il n’est pas inutile de découvrir quelques notions hors programme de dénombrement afin de se trouver plus à l’aise devant sa copie le jour J. Étudions alors les dérangements, une notion voisine des arrangements qui, elle, est pourtant dans le programme.
Concept de dérangement en mathématiques
Définition d’un dérangement
On appelle dérangement d’un ensemble fini \(\mathbb{E}\) toute permutation de \(\mathbb{E}\) sans point fixe. Dit autrement, un dérangement de \(\mathbb{E}\) désigne toute bijection \(\eta\) de \(\mathbb{E}\) dans \(\mathbb{E}\) telle que, \(\forall x \in\mathbb{E} \) , \(\eta\) (x) est différent de x.
En notant \( n = \text{Card}{(E)} \), puisque \(\mathbb{E}\) est en effet un ensemble fini, c’est-à-dire admettant un cardinal, il est légitime de se demander quel est le nombre de dérangements dans \(\mathbb{E}\).
Un premier cas particulier
Approchons déjà le problème pour n = 3 afin de bien comprendre le rôle de la bijection notée ici \(\eta\).
Supposons que l’on ait \(\eta [1,2,3] = [3,2,1]\), alors \(\eta\) n’est pas une permutation sans point fixe, car le chiffre 2 est resté en deuxième dans les valeurs d’arrivée. À l’inverse, si \(\eta [1,2,3] = [3,1,2]\), alors \(\eta\) est bien un dérangement, car le chiffre 1 n’est plus en première position, idem pour 2 et 3. Il faut donc être conscient que, de la même manière que lorsque l’on travaille avec les arrangements, il s’agit de listes ordonnées.
En réalité, on remarque que pour cette liste \([1,2,3]\), il n’y a que deux dérangements possibles : \([2,3,1] \) et \([3,1,2] \). En effet, pour placer le premier chiffre dans la première case, il s’agit nécessairement d’un 2 ou d’un 3 (car pas de point fixe). Si on a choisi un 2, le chiffre de la deuxième case est nécessairement un 3 pour que le 3 ne soit pas sur la troisième case (pour éviter le point fixe). Donc, le 1 se retrouve à la fin. En commençant par 2, il n’y a donc qu’une seule possibilité et idem en commençant par 3. Soit exactement deux dérangements dans un ensemble de cardinal 3.
Mais qu’en est-il dans le cas général d’un ensemble de cardinal \(n\) ?
Calcul du nombre de dérangements dans le cas général du dénombrement
Soit \(\mathbb{E}\) un ensemble fini tel que \( \text{Card}{(E)}=n \). Dans ce cas général, on peut appréhender le problème de la manière suivante (appelé problème de Montmort et posé par le mathématicien Eugène Charles Catalan) : n personnes laissent leur chapeau au vestiaire ; lorsqu’elles viennent les chercher, chacune d’entre elles prend un chapeau au hasard ; quelle est la probabilité qu’aucune d’entre elles ne porte son chapeau à la sortie ?
Pour comprendre la preuve, il est nécessaire d’introduire la formule du crible généralisé. La formule du crible de Poincaré est au programme pour deux ensembles, mais ne l’est pas pour \(n\). Il n’est pas nécessaire de connaître par cœur cette formule, mais il peut être intéressant de la comprendre.
Notons \(\forall i \in [\![1,n]\!] , A_i\) l’ensemble des permutations qui laissent \(i\), le \(i\)-ème élément du vecteur de E invariant (\(i\) est donc un point fixe).
Alors, d’après la formule du crible généralisé, on a : \[\text{Card}(\displaystyle\bigcup_{k=1}^{n} A_{k}) = \displaystyle \sum_{k=1}^{n} (-1)^{(k-1)}\displaystyle \sum_{1\le i_1\le i_2\le …\le i_k\le n}\text{Card} (\displaystyle\bigcap_{j=1}^{k} {(A_i)}_j)\]
Ensuite, étant donné que l’on ne veut aucun point fixe, on cherche : \(\text{Card}(\displaystyle\bigcap_{k=1}^{n} \overline{A_{k}}) = n! – \text{Card}(\displaystyle\bigcup_{k=1}^{n} A_{k})\). En effet, le nombre de permutations sans aucun point fixe est égal au nombre total de permutations (qui vaut \(n!\) d’après le cours) soustrait au nombre de permutations admettant au moins un point fixe. Aidons-nous à présent de la formule du crible généralisé pour calculer ce second terme !
Notons par souci de simplification : \(S_k = \displaystyle \sum_{1\le i_1\le i_2\le …\le i_k\le n}\text{Card} (\displaystyle\bigcap_{j=1}^{k} {(A_i)}_j)\).
Dans \(\text{Card} (\displaystyle\bigcap_{j=1}^{k} {(A_i)}_j)\), on fixe les éléments de la liste jusqu’au \(k\)-ième élément et on permute les autres (c’est-à-dire ceux compris entre \(k\) et \(n\)). D’après le cours, il y a \(n-k\) façons de permuter un ensemble à \(n-k\) éléments.
Ainsi, \(\text{Card}(\displaystyle\bigcup_{k=1}^{n} A_{k}) = \displaystyle \sum_{k=1}^{n} (-1)^{(k-1)}\displaystyle \sum_{1\le i_1\le i_2\le …\le i_k\le n} (n-k)!\)
Par linéarité de la somme, puisque \((n-k)!\) ne dépend pas de l’indice \(i\), on a alors :
\(\text{Card}(\displaystyle\bigcup_{k=1}^{n} A_{k}) = \displaystyle \sum_{k=1}^{n} (-1)^{(k-1)}(n-k)!\displaystyle \sum_{1\le i_1\le i_2\le …\le i_k\le n} 1\).
Or, \(\sum_{1\le i_1\le i_2\le …\le i_k\le n} 1 = {{n}\choose{k}} \) et comme \({{n}\choose{k}} \times (n-k)! = \frac{n!}{k!}\), on conclut que :
\(\text{Card}(\displaystyle\bigcup_{k=1}^{n} A_{k}) = n! \times \displaystyle \sum_{k=1}^{n} \frac{(-1)^{(k-1)}}{k!} \)
En remobilisant l’expression de départ qui donne le nombre de dérangements, on a :
\(\text{Card}(\displaystyle\bigcap_{k=1}^{n} \overline{A_{k}}) = n! – n! \times \displaystyle \sum_{k=1}^{n} \frac{(-1)^{(k-1)}}{k!} = n! \times ( 1 +\displaystyle \sum_{k=1}^{n} \frac{(-1)^{k}}{k!}) \)
Et comme le terme de la somme pour \( k = 0\) vaut 1, on obtient finalement que le nombre de dérangements dans un ensemble \(\mathbb{E}\) de cardinal \(n\) vaut :
\[\large { n! \displaystyle \sum_{k=0}^{n} \frac{(-1)^{k}}{k!}} \]
Notion de sous-factorielle
On peut également exprimer ce résultat à l’aide de la notion de sous-factorielle. En effet, le nombre de dérangements dans un ensemble à n éléments vaut \(!n = n! \displaystyle \sum_{k=0}^{n} \frac{(-1)^{k}}{k!} \) (attention à la place du point d’exclamation). Voilà pour le point de culture mathématique !
Conséquences de ce résultat en probabilité/dénombrement
En notant \({(D_n)}_{n \in\mathbb{N}}\) le nombre de dénombrements, il est possible d’étudier la probabilité qu’une permutation soit en fait un dérangement (évènement noté ici \(\delta_n\)). Par équiprobabilité, une telle probabilité est égale au nombre de dérangements sur le nombre total de permutations. Autrement dit, cette probabilité vaut :
\(P(\delta_n)= \frac{n!\displaystyle \sum_{k=0}^{n} \frac{(-1)^{k}}{k!}}{n!} = \displaystyle \sum_{k=0}^{n} \frac{(-1)^{k}}{k!}\)
Quelle est dès lors la limite d’une telle probabilité ?
\(\lim \limits_{n \to +\infty} P(\delta_n) =\displaystyle \sum_{k=0}^{+\infty} \frac{(-1)^k}{k!} = e^{-1} \) (on reconnaît en effet une série exponentielle toujours convergente de somme \(e^{-1}\) ici).
Interprétation
Réutilisons le cadre du problème de Montmort. Si une infinité de personnes posent leur chapeau dans un vestiaire et que tout le monde repart à la fin avec un chapeau au hasard, la probabilité que personne ne reparte avec son propre chapeau tend vers \(\frac{1}{e}\). Très beau résultat n’est-ce pas ?
Un problème annexe aux dérangements en Python
Comment peut-on vérifier à partir de deux listes de nombres que l’une est bien une permutation de l’autre ? En supposant que les deux listes soient issues d’un même ensemble de cardinal n ?
Supposons ici que l’on dispose de deux listes (vecteurs en Python), notées A et B, d’un même ensemble E et que l’on cherche à savoir si l’une est un dérangement de l’autre. On compare alors chaque valeur des deux listes pour savoir si un chiffre se répète à un moment dans les deux listes. On a donc le code suivant :
Ici, on réalise un test pour chaque élément des deux vecteurs. Si à un moment, la valeur de rang k du vecteur A est identique à celle du vecteur B, alors il ne s’agit pas réellement d’un dérangement et donc on demande de retourner False. Si ce n’est jamais le cas, le code renvoie True.
Retrouve une application de cette notion de dérangement sur le sujet ESSEC Maths II 2004 (ECS).
Conclusion
La notion de dérangement est donc assez complexe à appréhender et permet d’aller plus loin en vue de la préparation des Parisiennes. Elle fait en effet intervenir une compréhension fine des notions de dénombrement, avec de longs calculs. Avant tout, il convient de s’assurer de la parfaite maîtrise des notions de dénombrement présentes dans le programme afin de pouvoir aborder la notion de dérangement. Voici un lien vers un article qui permet de s’exercer sur ces notions plus classiques.
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !