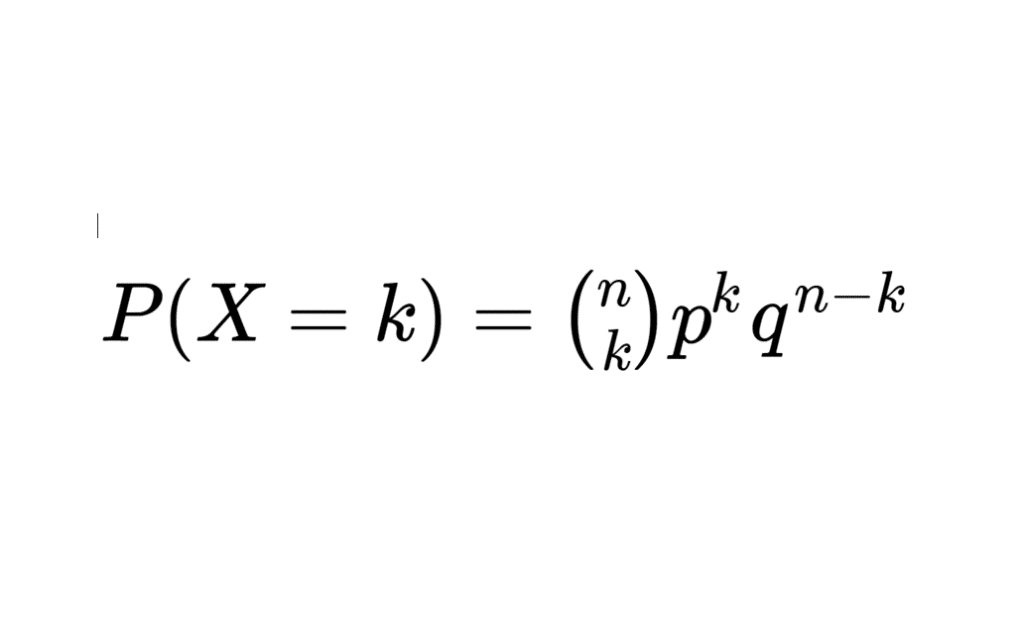La loi binomiale est un grand classique du concours. Il est donc nécessaire de maîtriser les bases, mais aussi les plus fines subtilités de cette notion. Major-Prépa est là pour t’aider. Voici ce qu’il y a à savoir. On prendra pour tout le long de cet article \( n \in \mathbb{N}\)et \( p \in \mathbb{[0,1]}\).
La loi binomiale expliquée en français
Dans un énoncé, la loi binomiale est souvent très explicitement énoncée. Il est donc facile de la repérer. En effet, la loi binomiale se définie ainsi : si X suit une loi binomiale de paramètres n et p, alors X compte le nombre de succès lors de n épreuves de Bernoulli indépendantes de paramètre p.
Exemple concret
Prenons une pièce truquée qui donne pile avec une probabilité de 1/3. Soit X la variable aléatoire qui compte le nombre de piles lors de 47 lancers de cette pièce. Alors, \(X \hookrightarrow\mathcal{B}(47,1/3)\).
La définition mathématique
On pose q = 1 – p. Soit X une variable aléatoire. On dit que X suit une loi binomiale de paramètres n et p, et l’on note \(X \hookrightarrow\mathcal{B}(n,p)\) lorsque : \(X (\Omega) = [\![0,n]\!] \; et \; \forall k \in [\![0,b]\!], P(X = k) = {{n}\choose{k}} p^{k}q^{n-k}\).
Quelques propriétés sur la loi binomiale
Démonstration de l’espérance et de la variance
Le support de la loi binomiale étant fermé, elle admet des moments de tous ordres.
\begin{align}
\text{On a :} \quad \mathbb{E}(X) &= \sum_{k=1}^{n} k P(X=k) \\
&= \sum_{k=1}^{n} k \binom{n}{k} p^{k} (1-p)^{n-k} \\
&= \sum_{k=1}^{n} n \binom{n-1}{k-1} p^{k} (1-p)^{n-k} \quad \text{par la formule du capitaine} \\
&= n \sum_{k=0}^{n-1} \binom{n-1}{k} p^{k+1} (1-p)^{n-1-k} \quad \text{par changement de variable} \\
&= np \sum_{k=0}^{n-1} \binom{n-1}{k} p^{k} (1-p)^{n-1-k} \\
&= np (p + (1-p))^{n-1} \\
&= np \\
\end{align}
Donc : \( \fbox{\(E(X) = np\)}\)
Soit \(n \geq 2\).\begin{align}
\text{On a :} \quad \mathbb{E}(X^2) &= \sum_{k=0}^{n} k^2 P(X=k) \\
&= \sum_{k=0}^{n} k^2 \binom{n}{k} p^{k} (1-p)^{n-k} \\
&= \sum_{k=0}^{n} nk \binom{n-1}{k-1} p^{k} (1-p)^{n-k} \quad \text{par la formule du capitaine} \\
&= n \sum_{k=0}^{n-1} (k+1) \binom{n-1}{k} p^{k+1} (1-p)^{n-1-k} \quad \text{par changement de variable} \\
&= n \sum_{k=0}^{n-1} k \binom{n-1}{k} p^{k+1} (1-p)^{n-1-k} + n \sum_{k=0}^{n-1} \binom{n-1}{k} p^{k+1} (1-p)^{n-1-k} \\
&= n \sum_{k=1}^{n-1} (n-1) \binom{n-2}{k-1} p^{k+1} (1-p)^{n-1-k} + np \sum_{k=0}^{n-1} \binom{n-1}{k} p^{k} (1-p)^{n-1-k} \\
&= n(n-1) \sum_{k=0}^{n-2} \binom{n-2}{k} p^{k+2} (1-p)^{n-2-k} + np \\
&= n(n-1)p^2 \sum_{k=0}^{n-2} \binom{n-2}{k} p^{k} (1-p)^{n-2-k} + np \\
&= n(n-1)p^2 (p + (1-p))^{n-2} + np \\
&= n(n-1)p^2 + np
\end{align}
Donc : \( \mathbb{E}(X^2) = n(n-1)p^2 + np \).
Or, \( \text{Var}(X) = \mathbb{E}(X^2) – (\mathbb{E}(X))^2 \).
Donc,
\[
\text{Var}(X) = n(n-1)p^2 + np – (np)^2 = n(n-1)p^2 + np – n^2p^2 = np – np^2.
\]
C’est-à-dire \( \boxed{\text{Var}(X) = np(1-p)} \).
Ce qu’il faut savoir pour avoir le top 5
Stabilité de la loi binomiale (extension de la stabilité de la loi de Bernoulli)
La loi binomiale est stable. En effet, soit \(X \hookrightarrow\mathcal{B}(n,p)\) et \(Y \hookrightarrow\mathcal{B}(m,p)\) avec \( n \in \mathbb{N}\). Alors \(X + Y \hookrightarrow\mathcal{B}(n + m,p)\).
Cela se prouve par calcul ou car X + Y compte le nombre de succès lors de n + m épreuves de Bernoulli indépendantes.
Application de la loi faible des grands nombres
Soit \((X_n)_{n \in \mathbb{N}}\) une suite de variables aléatoires indépendantes et identiquement distribuées suivant une loi de Bernoulli de paramètre \(p\). Alors, par la loi faible des grands nombres :
\[
\frac{\displaystyle \sum_{k=1}^{n} X_k}{n} \overset{\mathbb{P}}{\rightarrow} p.
\]
En notant \(Y_n = \frac{\displaystyle \sum_{i=1}^{n} X_i}{n}\), alors \(Y_n \sim \mathcal{B}(n,p)\). On a donc :
\[
\frac{Y_n}{n} \overset{\mathbb{P}}{\rightarrow} p.
\]
Application du théorème central limite
Puisque les \(X_i\) admettent un moment d’ordre 2 et que les \(X_i\) sont deux à deux indépendantes, par le théorème central limite, on a :
\[
\frac{\displaystyle \sum_{i=1}^{n} X_i – np}{\sqrt{np(1-p)}} \overset{\mathcal{L}}{\rightarrow} N
\]
où \(N \sim \mathcal{N}(0,1)\).
Donc, avec les mêmes notations, on obtient :
\[
\frac{Y_n – np}{\sqrt{np(1-p)}} \overset{\mathcal{L}}{\rightarrow} N
\]
où \(N \sim \mathcal{N}(0,1)\)
Approximation de la loi binomiale par la loi de Poisson
Soit \((X_n)_{n \in \mathbb{N}}\) une suite de variables aléatoires suivant une loi binomiale de paramètres \(n\) et \(p_n\). On suppose que \( \lim_{n \to +\infty} np_n = \lambda \). Alors :
\[
(X_n) \overset{\mathcal{L}}{\rightarrow} Y
\]
où \(Y \sim \mathcal{P}(\lambda)\)
Dans un cas pratique, on peut utiliser ce théorème lorsque \(n\) est « grand » et \(p\) est « petit », c’est-à-dire, lorsque
\[
n \geq 30, \quad p \leq 0,1, \quad \text{et} \quad np \leq 15.
\]
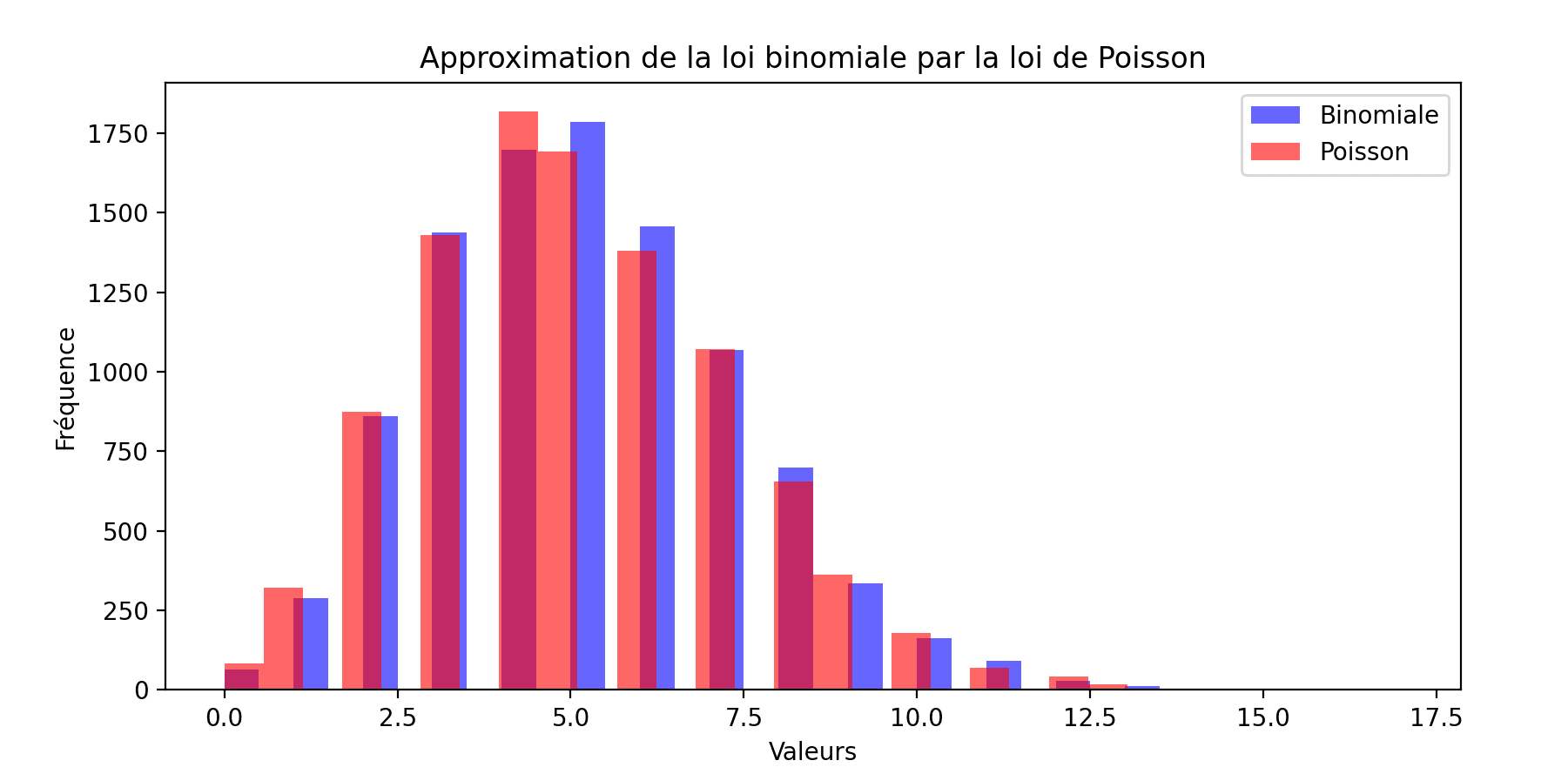
Et voici comment on peut approximer grâce à Python la loi binomiale par la loi de Poisson.
On importe ce dont on a besoin et on donne des valeurs cohérentes :
Puis on fait des réalisations d’une loi binomiale et d’une loi de Poisson et on rentre ces résultats dans des histogrammes :
Un peu de légendes…
Le graphe qui apparaît montre ainsi qu’il y a une forte corrélation entre la loi binomiale et la loi de Poisson lorsque n est « grand » et que p est « petit ».
Notions hors programme en rapport avec la loi binomiale
La loi binomiale a donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver :
- La loi binomiale négative
- La loi de Pascal
- La loi trinomiale
- La loi multinomiale (qui n’est autre que la généralisation de la loi binomiale)
Les sujets en rapport avec la loi binomiale
Avec ça, tu pourras performer au concours sur la loi binomiale. Je te conseille de faire aussi des annales à fond :
- EDHEC 2008
- Math II 2014
- Pour les plus courageux, la loi binomiale négative, EDHEC 2003 (voie ECS/appro)
Tu peux aussi aller voir nos autres articles pour maîtriser les autres variables aléatoires :
- Les probabilités discrètes en général
- Les variables aléatoires symétriques
- La formule du crible de Poincaré itérée
N’hésite pas à consulter toutes nos ressources mathématiques !