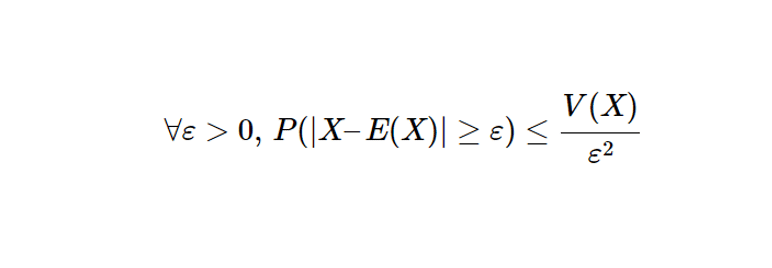L’inégalité de Bienaymé-Tchebychev paraît impressionnante, mais il est essentiel de la connaître. Cet article te permettra de réviser toutes les méthodes à maîtriser en rapport avec cette formule. Tu feras ainsi la différence face aux autres candidats qui ne savent pas l’appliquer ou qui n’ont tout simplement pas appris cette formule.
L’inégalité de Bienaymé-Tchebychev
Soit \( X \) une variable aléatoire discrète admettant un moment d’ordre 2. On a :
\[
\forall \varepsilon > 0, \quad \mathbb{P}\left(|X – \mathbb{E}(X)| \geq \varepsilon\right) \leq \frac{V(X)}{\varepsilon^2},
\]
Démonstration de l’inégalité
\begin{align*}
\mathbb{P}\left(|X – \mathbb{E}(X)| \geq \varepsilon\right) &= \mathbb{P}\left((X – \mathbb{E}(X))^2 \geq \varepsilon^2\right) \quad \text{car } x \mapsto x^2 \text{ réalise une bijection de } \mathbb{R}^+ \text{ dans } \mathbb{R}^+\\
&\leq \frac{\mathbb{E}\left[(X – \mathbb{E}(X))^2\right]}{\varepsilon^2} \quad \text{par l’inégalité de Markov car}(X – \mathbb{E}(X))^2 \text{admet un moment d’ordre 2} \\
&\leq \frac{V(X)}{\varepsilon^2},
\end{align*}
Donc : \[\boxed{
\mathbb{P}\left(|X – \mathbb{E}(X)| \geq \varepsilon\right) \leq \frac{V(X)}{\varepsilon^2}
}\]
Voici quelques exemples d’application de la formule de Bienaymé-Tchebychev.
Lorsqu’une inégalité est donnée
Énoncé
En notant \(\Phi\) la fonction de répartition d’une loi normale centrée réduite, prouver que pour tout x > 0 , \(1-\Phi(x) \geq \frac{1}{2x^2}\)
Correction
Soit \( x > 0 \)
\[
\begin{align*}
\mathbb{P}(|X| \ge x) &= 1 – \mathbb{P}(|X| \le x) \quad \text{car X est à densité} \\
&= 1 – (\Phi(x) – \Phi(-x)) \\
&= 1 – (\Phi(x) – (1 – \Phi(x))) \\
&= 2(1 – \Phi(x))
\end{align*}
\]
Donc
\[
\begin{align*}
1 – \Phi(x) &= \frac{1}{2}\mathbb{P}(|X| \ge x) \\&= \frac{1}{2}\mathbb{P}(|X – \mathbb{E}(X)| \ge x) \quad \text{car E(X) = 0}\\
&= \frac{1}{2} \frac{V(X)}{x^2} \quad \text{par l’inégalité de Bienaymé-Tchebychev car } X \text{ admet un moment d’ordre 2 par définition} \\ &= \frac{1}{2x^2} \quad \text{car V(X) = 1}
\end{align*}
\]
On a bien prouvé grâce à cette inégalité que :
\[
\boxed{\forall x > 0, 1 – \Phi(x) \le \frac{1}{2x^2}}
\]
Lorsqu’on prouve qu’un estimateur est convergent avec l’inégalité de Bienaymé-Tchebychev
Prenons \( X_n\) un estimateur de \( \Theta \) admettant un moment d’ordre 2. Si \( X_n \) est sans biais et que \( \lim \limits_{n \to +\infty} V(X_n) = 0\), alors par l’inégalité de Bienaymé-Tchebychev,
\[ X_n \overset{\mathbb{P}}{\rightarrow} \Theta. \]
En effet, puisque \( \mathbb{E}(X_n) = \Theta\), alors par l’inégalité de Bienaymé-Tchebychev :
\[ \forall \varepsilon > 0, \, \mathbb{P}(|X_n – \Theta| \geq \varepsilon) \leq \frac{V(X_n)}{\varepsilon^2}. \]
Or,
\[ \forall \varepsilon > 0, \, \lim \limits_{n \to +\infty} \frac{V(X_n)}{\varepsilon^2} = 0. \]
Donc,
\[ \forall \varepsilon > 0, \, \lim \limits_{n \to +\infty} \mathbb{P}(|X_n – \Theta| \geq \varepsilon) = 0 \quad \text{par le théorème des gendarmes}. \]
Ce qui prouve bien que :
\[ \boxed{ X_n \overset{\mathbb{P}}{\rightarrow} \Theta } \quad \text{et donc que } X_n \text{ est un estimateur convergent de } \Theta. \]
La loi faible des grands nombres
La condition suffisante précédente permet de démontrer la loi faible des grands nombres.
Rappel de la loi faible des grands nombres
Soit \( (X_n)_{n \in \mathbb{N}^*} \) une suite de variables aléatoires indépendantes, possédant une même espérance notée \( m \) et la même variance \( \sigma^2 \).
Alors,
\[ \left( \frac{1}{n} \sum_{k=1}^{n} X_k \right) \overset{\mathbb{P}}{\rightarrow} m. \]
Démonstration de la loi faible des grands nombres
\[\begin{align} \mathbb{E}(\frac{1}{n} \sum_{k=1}^{n} X_k) &= \frac{1}{n}\sum_{k=1}^{n} \mathbb{E}(X_k)\\&=\frac{1}{n}\sum_{k=1}^{n} m\\ &= \frac{nm}{n} \\&=m\end{align}\]
Donc : \(\frac{1}{n}\sum_{k=1}^{n} X_k\) est un estimateur sans biais de m.
\[
\begin{align}
V\left(\frac{1}{n} \sum_{k=1}^{n} X_k\right) &= \frac{1}{n^2} \sum_{k=1}^{n} V(X_k) \\
&= \frac{1}{n^2} \sum_{k=1}^{n} \sigma^2 \\
&= \frac{\sigma^2}{n} \\
&\underset{n \to +\infty}{\rightarrow} 0
\end{align}
\]
Ce cas respecte donc les conditions pour prouver qu’un estimateur est convergent et donc \[
\boxed{
\left( \frac{1}{n} \sum_{k=1}^{n} X_k \right) \overset{\mathbb{P}}{\rightarrow} m.
}
\]
Lorsqu’on construit un intervalle de confiance à l’aide de l’inégalité de Bienaymé-Tchebychev
Bienaymé-Tchebychev est souvent très utile pour construire des intervalles de confiance. Voici une démonstration de cours qui te permettra de comprendre comment utiliser l’inégalité de Bienaymé-Tchebychev et de réviser la construction d’un intervalle de confiance.
Énoncé du cours
Soit \( n \in \mathbb{N} \). Soit \( X \sim B(p) \). On pose \( (X_i)_{1 \leq i \leq n} \) des variables indépendantes et identiquement distribuées de même loi que \( X \). Soit \( \overline{Y}_n \) la moyenne empirique des \( X_i \).
Alors :
\[ \left[ \overline{Y}_n – \sqrt{\frac{1}{2n\alpha}}, \overline{Y}_n + \sqrt{\frac{1}{2n\alpha}} \right] \]
est un intervalle de confiance pour \( p \) au niveau de confiance \( 1 – \alpha \).
Démonstration
Soit \( \epsilon > 0 \). On a :
\[
\begin{align}
& \mathbb{P}\left(\left| \overline{Y}_n – p \right| \ge \epsilon\right) \le \frac{p(1-p)}{n\epsilon^2} \quad \text{par l’inégalité de Bienaymé-Tchebychev} \\
& \Leftrightarrow 1 – \mathbb{P}\left(\overline{Y}_n – \epsilon \le p \le \overline{Y}_n + \epsilon\right) \le \frac{p(1-p)}{n\epsilon^2} \\
& \Leftrightarrow 1 – \mathbb{P}\left(\overline{Y}_n – \epsilon \le p \le \overline{Y}_n + \epsilon\right) \le \frac{1}{4n\epsilon^2} \quad \text{par l’étude de la fonction } x \mapsto x(1-x) \text{ dans l’intervalle } [0,1]. \\
& \Leftrightarrow \mathbb{P}\left(p \in [\overline{Y}_n – \epsilon, \overline{Y}_n + \epsilon]\right) \ge 1 – \frac{1}{4n\epsilon^2}.
\end{align}
\]
Et on cherche \[ 1 – \frac{1}{4n\epsilon^2} = 1 – \alpha\]
Donc, \[\epsilon = \frac{1}{2}\sqrt{\frac{1}{n\alpha}}\]
En remplaçant \( \epsilon \), on obtient que :
\[
\mathbb{P}\left(p \in \left[ \overline{Y}_n – \frac{1}{2}\sqrt{\frac{1}{n\alpha}}, \, \overline{Y}_n + \frac{1}{2}\sqrt{\frac{1}{n\alpha}} \right] \right) \ge 1 – \alpha.
\]
C’est bien ce qu’il fallait démontrer.
Bienaymé-Tchebychev dans les sujets de concours
Voici une liste non exhaustive de sujets :
Notre cher Pafnouti Tchebychev a aussi donné son nom à des polynômes, ne l’oublions pas. N’hésite pas à consulter toutes nos autres ressources mathématiques.