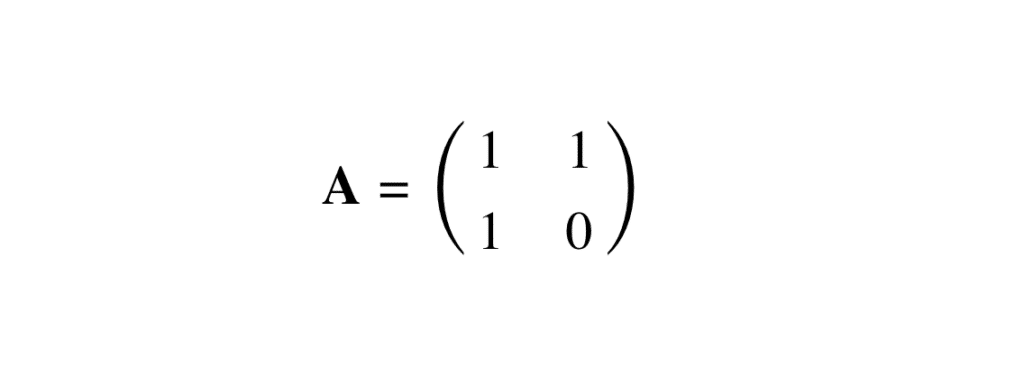Les matrices de Fibonacci constituent un sujet fascinant en mathématiques, se situant à la croisée de l’algèbre linéaire et de la théorie des nombres. Leur étude permet de comprendre plus en profondeur les célèbres nombres de Fibonacci (dont le nombre d’or) et leurs propriétés. En effet, les nombres de Fibonacci apparaissent dans divers contextes mathématiques, allant de la théorie des nombres à la géométrie, et même en biologie où ils décrivent des motifs de croissance naturelle. Les matrices de Fibonacci offrent une perspective algébrique puissante pour analyser et généraliser ces nombres, permettant ainsi des calculs plus efficaces et des démonstrations plus élégantes de leurs propriétés.
Cet article explore les matrices de Fibonacci, leurs propriétés et leurs applications, tout en fournissant des exemples pour illustrer les concepts. Nous examinerons comment ces matrices peuvent être utilisées pour générer les termes de la suite de Fibonacci (du célèbre mathématicien Leonardo Fibonacci), ainsi que leur lien avec les transformations linéaires et les valeurs propres.
Définition des matrices de Fibonacci
Pour commencer, définissons les matrices de Fibonacci. La suite de Fibonacci est une suite d’entiers où chaque terme est la somme des deux termes précédents, avec \( F_0 = 0 \) et \( F_1 = 1 \). Formellement, on a :
\[ F_n = F_{n-1} + F_{n-2} \]
La matrice de Fibonacci est définie comme suit :
\[
\mathbf{A} = \begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\]
L’intérêt de cette matrice réside dans sa capacité à générer les termes de la suite de Fibonacci par multiplication matricielle. En effet, on peut démontrer que :
\[
\mathbf{A}^n = \begin{pmatrix}
F_{n+1} & F_n \\
F_n & F_{n-1}
\end{pmatrix}
\]
Preuve par récurrence
Nous prouvons cette propriété par récurrence. Pour \( n = 1 \), on a :
\[
\mathbf{A} = \begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix} = \begin{pmatrix}
F_2 & F_1 \\
F_1 & F_0
\end{pmatrix}
\]
Supposons la propriété vraie pour \( n = k \), c’est-à-dire :
\[
\mathbf{A}^k = \begin{pmatrix}
F_{k+1} & F_k \\
F_k & F_{k-1}
\end{pmatrix}
\]
Pour \( n = k+1 \), nous devons montrer que :
\[
\mathbf{A}^{k+1} = \mathbf{A}^k \mathbf{A}
\]
En effectuant la multiplication matricielle, nous obtenons :
\[
\mathbf{A}^{k+1} = \begin{pmatrix}
F_{k+1} & F_k \\
F_k & F_{k-1}
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix} = \begin{pmatrix}
F_{k+1} + F_k & F_{k+1} \\
F_k + F_{k-1} & F_k
\end{pmatrix}
\]
En utilisant la définition de la suite de Fibonacci \( F_{k+2} = F_{k+1} + F_k \) et \( F_{k+1} = F_k + F_{k-1} \), nous avons :
\[
\mathbf{A}^{k+1} = \begin{pmatrix}
F_{k+2} & F_{k+1} \\
F_{k+1} & F_k
\end{pmatrix}
\]
Ainsi, la propriété est vraie pour \( n = k+1 \). Par récurrence, la formule est démontrée pour tout entier naturel \( n \).
Propriétés des matrices de Fibonacci
Les matrices de Fibonacci possèdent plusieurs propriétés intéressantes. Explorons-en quelques-unes.
Trace et déterminant
La trace d’une matrice est la somme de ses éléments diagonaux. Pour la matrice de Fibonacci \(\mathbf{A}\), la trace est :
\[
\text{tr}(\mathbf{A}) = 1 + 0 = 1
\]
Le déterminant de \(\mathbf{A}\) est :
\[
\det(\mathbf{A}) = (1 \cdot 0) – (1 \cdot 1) = -1
\]
De manière générale, pour toute puissance \( n \) de la matrice de Fibonacci \(\mathbf{A}\), on peut montrer que :
\[
\det(\mathbf{A}^n) = (-1)^n
\]
Valeurs propres et vecteurs propres
Les valeurs propres de \(\mathbf{A}\) sont les racines du polynôme caractéristique :
\[
\det(\mathbf{A} – \lambda \mathbf{I}) = \det \begin{pmatrix}
1 – \lambda & 1 \\
1 & -\lambda
\end{pmatrix} = \lambda^2 – \lambda – 1 = 0
\]
Les solutions de cette équation sont les valeurs propres :
\[
\lambda_{1,2} = \frac{1 \pm \sqrt{5}}{2}
\]
Ces valeurs sont connues sous les noms de nombre d’or \( \displaystyle \varphi = \frac{1 + \sqrt{5}}{2}\) et son conjugué \( \displaystyle \overline{\varphi} = \frac{1 – \sqrt{5}}{2}\).
Les vecteurs propres associés sont :
\[
\mathbf{v}_1 = \begin{pmatrix}
\varphi \\
1
\end{pmatrix}, \quad \mathbf{v}_2 = \begin{pmatrix}
\overline{\varphi} \\
1
\end{pmatrix}
\]
Applications des matrices de Fibonacci
Les matrices de Fibonacci trouvent des applications dans divers domaines tels que la théorie des nombres, la cryptographie et les algorithmes de calcul.
Calcul rapide des nombres de Fibonacci
Une application pratique des matrices de Fibonacci est le calcul rapide des nombres de Fibonacci. En utilisant la propriété \(\mathbf{A}^n\), on peut calculer \(F_n\) en temps logarithmique par exponentiation rapide des matrices, ce qui est beaucoup plus efficace que l’algorithme naïf.
Relations avec la suite de Fibonacci
Les matrices de Fibonacci permettent de généraliser et de découvrir de nouvelles propriétés de la suite de Fibonacci. Par exemple, on peut montrer que la somme des \(n\) premiers nombres de Fibonacci est donnée par :
\[
\sum_{i=1}^{n} F_i = F_{n+2} – 1
\]
Cette relation peut être démontrée en utilisant des techniques matricielles.
Formule de Binet et matrices de Fibonacci
La formule de Binet permet de calculer directement le \(n\)-ième terme de la suite de Fibonacci sans avoir à calculer tous les termes précédents. Cette formule utilise les valeurs propres de la matrice de Fibonacci \(\mathbf{A}\). Les valeurs propres \(\lambda_1\) et \(\lambda_2\) de \(\mathbf{A}\) sont données par :
\[
\lambda_{1,2} = \frac{1 \pm \sqrt{5}}{2}
\]
La formule de Binet s’exprime alors comme suit :
\[
F_n = \frac{\lambda_1^n – \lambda_2^n}{\lambda_1 – \lambda_2}
\]
En utilisant les valeurs propres, on peut également diagonaliser la matrice \(\mathbf{A}\) :
\[
\mathbf{A} = \mathbf{P} \mathbf{D} \mathbf{P}^{-1}
\]
où \(\mathbf{D}\) est une matrice diagonale contenant les valeurs propres de \(\mathbf{A}\) et \(\mathbf{P}\) est la matrice de passage formée par les vecteurs propres de \(\mathbf{A}\).
Relation avec la suite de Lucas
La suite de Lucas est une généralisation des suites de Fibonacci. Elle est définie par une relation de récurrence similaire :
\[
L_n = L_{n-1} + L_{n-2}
\]
avec \(L_0 = 2\) et \(L_1 = 1\). Les termes de la suite de Lucas peuvent également être exprimés à l’aide de matrices. En particulier, la matrice de Fibonacci \(\mathbf{A}\) peut être utilisée pour générer les termes de la suite de Lucas :
\[
\mathbf{A}^n = \begin{pmatrix}
L_{n+1} & L_n \\
L_n & L_{n-1}
\end{pmatrix}
\]
Exponentiation matricielle et calcul rapide des puissances de matrices
L’exponentiation rapide est une technique efficace pour calculer des puissances de matrices. Elle repose sur la décomposition binaire de l’exposant. Pour calculer \(\mathbf{A}^n\) rapidement, on utilise l’algorithme de l’exponentiation rapide :
1. Si \(n = 0\), retourner l’identité \(\mathbf{I}\).
2. Si \(n\) est pair, calculer \(\mathbf{A}^{n/2}\), puis \((\mathbf{A}^{n/2})^2\).
3. Si \(n\) est impair, calculer \(\mathbf{A}^{n-1}\), puis \(\mathbf{A} \cdot \mathbf{A}^{n-1}\).
Cette méthode permet de réduire la complexité du calcul de \(\mathbf{A}^n\) de \(O(n)\) à \(O(\log n)\).
Décomposition LU de la matrice de Fibonacci
La décomposition LU d’une matrice est une factorisation sous la forme \(\mathbf{A} = \mathbf{L} \mathbf{U}\), où \(\mathbf{L}\) est une matrice triangulaire inférieure et \(\mathbf{U}\) est une matrice triangulaire supérieure. Pour la matrice de Fibonacci \(\mathbf{A}\), la décomposition LU est donnée par :
\[
\mathbf{L} = \begin{pmatrix}
1 & 0 \\
1 & 1
\end{pmatrix}, \quad \mathbf{U} = \begin{pmatrix}
1 & 1 \\
0 & -1
\end{pmatrix}
\]
Cette décomposition permet de résoudre efficacement des systèmes linéaires et d’inverser la matrice de Fibonacci.
Conclusion
Les matrices de Fibonacci offrent une manière élégante et puissante de comprendre et de manipuler la suite de Fibonacci. Leurs propriétés algébriques permettent non seulement de calculer efficacement les termes de la suite, mais aussi de découvrir de nouvelles relations et applications.
Ainsi, bien que les matrices de Fibonacci soient hors programme, la compréhension approfondie des propriétés liées à ces matrices te permettra d’améliorer tes compétences en algèbre linéaire et en analyse. L’étude de cette notion te préparera donc pour les épreuves écrites et orales.
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés ! Tu peux également accéder à toutes nos autres ressources mathématiques !