Dans cet article, tu vas apprendre à maîtriser la méthode des rectangles en Python pour approximer des valeurs d’intégrales et donner des encadrements de leur valeur exacte. Tu verras également les principales faiblesses de cette méthode et les autres manières possibles pour obtenir des approximations plus précises.
Introduction
Utilité de la méthode en Python
Bien que hors programme, la méthode des rectangles en Python fait partie des méthodes les plus simples pour approximer l’aire d’une intégrale. En effet, il existe bien la fonction « quad » qui permet de calculer plus directement des approximations d’intégrales, mais l’erreur commise est souvent trop grande. D’autant que cette fonction est très largement hors programme, tandis que la méthode des rectangles ne mobilise que les outils du programme d’ECG.
Dès lors, on comprend l’utilité de la méthode des rectangles même si, nous le verrons, il y a également des limites à celle-ci et des alternatives encore plus précises existent pour approximer des valeurs d’intégrales.
Rappel sur la méthode des rectangles
Un article y est déjà entièrement consacré sur Major-Prépa, tu peux donc le lire avant de chercher à comprendre comment un tel problème est transposable en Python. Voici le lien.
Le script commenté
Première approximation
Si tu as bien compris comment fonctionne sur papier la méthode des rectangles, alors nous pouvons nous lancer dans le script Python sans plus tarder. Ici, nous allons approximer \(\displaystyle \int_{a}^{b} f(t) \,\mathrm{d}t \) par le calcul de \(S_n\) définie par \(\forall n \in\mathbb{N} , S_n = \frac{b-a}{n} \times \displaystyle \sum_{k=0}^{n-1}f (a+k\times \frac{b-a}{n})\)
Voici un script possible :
On définit tout d’abord la longueur des intervalles (ligne 2). On initialise notre boucle à S=0 (quand il n’y a pas de rectangle, l’aire totale est évidemment nulle). Puis il n’y a plus qu’à sommer l’aire de chaque rectangle avec la formule qui remonte à nos premières années de collège (aire du rectangle = longueur \(\times\) largeur).
Exemple
Si nous cherchons à calculer \(\displaystyle \int_{0}^{1} t^2\,\mathrm{d}t\) par la méthode des rectangles, le programme précédent renvoie la valeur 0,33233399999999996 pour n=500. En calculant cette intégrale à la main, on sait que la valeur exacte est 1/3. Le résultat rendu n’est donc pas exact, mais fournit une très bonne approximation.
Encadrement de la valeur exacte de l’intégrale
Comme tu le sais déjà, dans la méthode des rectangles, on peut calculer \(S_n\) ou \(R_n\) où l’on a :
\[\forall n \in\mathbb{N} , S_n = \frac{b-a}{n} \times \displaystyle \sum_{k=0}^{n-1}f (a+k\times \frac{b-a}{n})\] et \[\forall n \in\mathbb{N} , R_n = \frac{b-a}{n} \times \displaystyle \sum_{k=0}^{n-1}f (a+(k+1)\times \frac{b-a}{n})\]
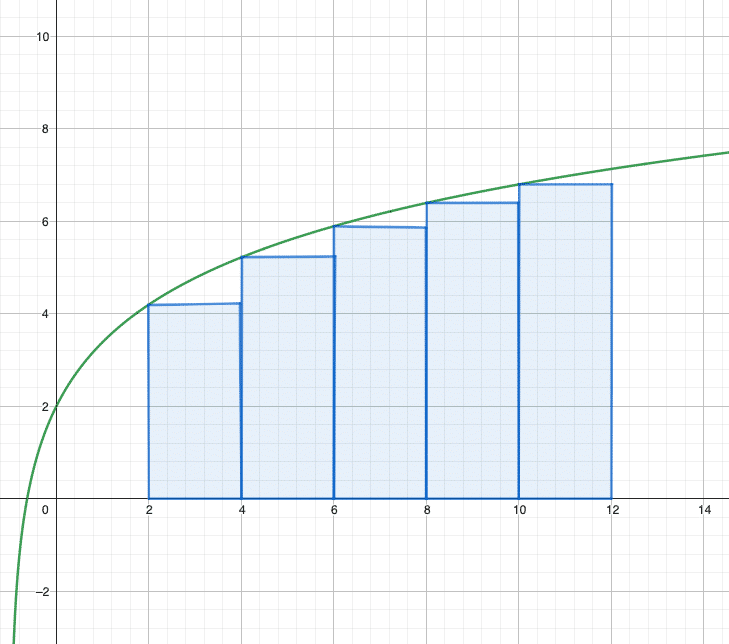
Or, \(S_n\) permet de donner une approximation de la valeur de l’intégrale par valeurs inférieures, tandis que \(R_n\) en donne une par valeurs supérieures (cela vaut seulement dans le cas d’une fonction croissante). Cela se comprend bien avec le graphique suivant :
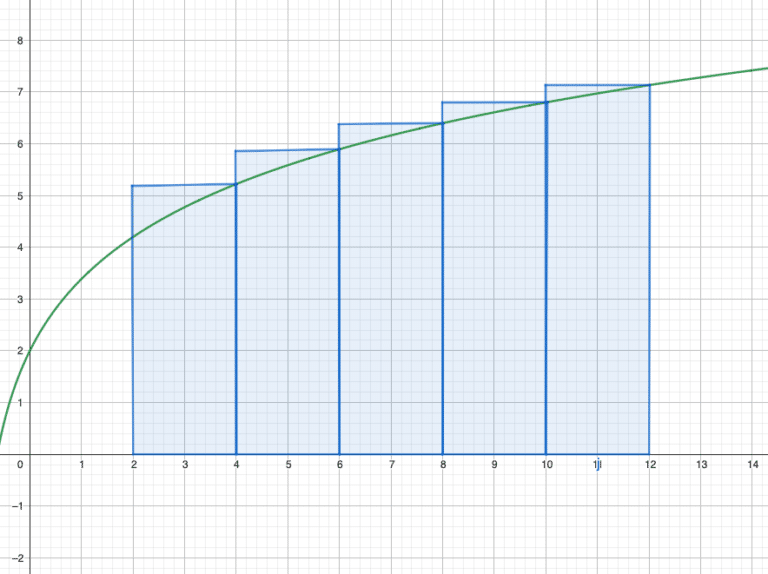
Le premier graphique montre la méthode des rectangles par valeurs supérieures et le deuxième par valeurs inférieures.
En effet, si \(f\) est croissante sur \([a,b]\), alors on a l’encadrement suivant :
\[\forall n \in\mathbb{N} , S_n \le\displaystyle \int_{a}^{b} f(t) \,\mathrm{d}t\le R_n\]
Si \(f\) est décroissante sur \([a,b]\), alors on inverse simplement le sens des inégalités.
On peut donc construire, à l’aide de ces deux méthodes, un encadrement de la valeur exacte de l’intégrale si \(f\) est monotone sur \([a,b]\). En réutilisant le premier code et en l’adaptant pour calculer non seulement \(S_n\) mais également \(R_n\), on obtient le script suivant :
Imaginons que nous cherchons à calculer la valeur de \(\displaystyle \int_{-1}^{1} t^3\,\mathrm{d}t\) où \(f : t \to t^3\) est bien monotone sur \(\mathbb{R}\).
On sait directement que cette intégrale est égale à \(0\) (fonction continue impaire intégrée sur des bornes opposées). En exécutant le script précédent pour n=100, on obtient : -0,3199999999999982 , 0,3200000000000021. On obtient donc un encadrement de la valeur exacte de l’intégrale.
Les limites et les alternatives à la méthode des rectangles
Limites de la méthode des rectangles
Le principal problème de cette méthode est la faible vitesse de convergence de la valeur approchée de l’intégrale vers la valeur exacte lorsque \(n\) devient de plus en plus grand.
Exemple
Retour avec \(\displaystyle \int_{-1}^{1} t^3\,\mathrm{d}t\) pour différentes valeurs de \(n\).
n=10 : -3,1999999999999993
n=100 :-0,3199999999999982
n=1 000 :-0,03199999999999933
On voit ici très clairement que lorsque l’on multiplie n par 10, alors le résultat est seulement environ 10 fois plus précis. Cette faible vitesse de convergence vers la valeur exacte de l’intégrale est donc le principal défaut de cette méthode.
Alternatives à la méthode des rectangles
Face aux limites de cette méthode des rectangles, il existe d’autres méthodes applicables en Python qui permettent de calculer de manière plus précise des approximations de valeurs d’intégrales (qu’elles le soient pour des mêmes valeurs de \(n\) ou que la vitesse de convergence vers la valeur réelle de l’intégrale soit plus rapide).
Cependant, ces autres méthodes sont plus difficiles à mettre en place en Python, ce qui atteste à nouveau que la principale qualité de la méthode des rectangles est sa relative simplicité dans le codage Python.
Première autre méthode : la méthode des trapèzes
Il y a par exemple la méthode des trapèzes (hors programme) qui consiste à remplacer les rectangles par des trapèzes pour mieux épouser la courbure de \(f\) et donc réduire l’erreur d’approximation.
Tu peux t’amuser à la programmer en Python si tu veux t’entraîner sur des programmes un peu plus techniques. Indice : dans notre cas, le trapèze est composé d’un triangle et d’un rectangle (cela se vérifie graphiquement puisque la base des trapèzes, c’est l’axe des abscisses), cela te sera utile dans le script.
Deuxième autre méthode : la méthode de Simpson
Cette méthode consiste à approximer l’intégrale à l’aide de la somme de valeurs de \(f\). Le script Python est ici beaucoup plus complexe et la méthode est complètement hors programme.
Troisième autre méthode : la méthode de Monte-Carlo
Cette méthode (présente dans le programme d’ECG) fait appel à la loi faible des grands nombres, donc aux probabilités, et est plus satisfaisante que la méthode des rectangles en termes de vitesse de convergence de l’approximation vers la valeur réelle de l’intégrale. Voici un article qui détaille la méthode de Monte-Carlo.
Conclusion
En définitive, la méthode des rectangles s’avère assez efficace en Python pour calculer les valeurs approchées d’intégrales, sans trop se compliquer au niveau du code Python. Toutefois, elle n’est pas totalement optimale en raison d’une faible vitesse de convergence vers la valeur réelle de l’intégrale et d’autres méthodes d’approximations sont possibles (méthodes de Monte-Carlo, de Simpson, des trapèzes). La méthode des rectangles reste quant à elle très proche du programme et peut être amenée à tomber en Python lors de sujets de Parisiennes notamment !
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !