Avec la transformation des programmes des prépas ECG et ECT, les langages informatiques tels que Python prennent toujours plus de place au sein des exercices proposés par les écoles lors des concours. On voit d’ailleurs un certain nombre d’algorithmes revenir de manière récurrente, comme l’algorithme de dichotomie. Celui-ci permet d’approcher une solution d’équation (généralement \( f(x) = 0\)) à travers une analyse graphique de cette même fonction \(f\). Si tu as du mal à comprendre le principe de cette méthode, alors cet article est fait pour toi !
Le principe de la méthode de dichotomie
La dichotomie permet de diviser un segment en petites zones de façon à se rapprocher de plus en plus d’une quantité à une précision \(\epsilon\) déterminée. Avec cette méthode, tu vas pouvoir trouver une quantité suffisamment proche d’un nombre réel connu comme \(\pi\) ou \(\sqrt{2}\). Le principe est donc qu’en déterminant une fonction \(f\), on peut réussir à approcher n’importe quel réel.
De manière plus précise, en Python, la méthode de dichotomie fonctionne principalement grâce au principe de substitution. On pose deux réels qui appartiennent au domaine de définition de \(f\), que nous allons progressivement substituer afin d’obtenir un encadrement à un certain niveau de précision de la solution de \(f(x)=0\).
Il faut donc premièrement s’assurer que l’équation admet une solution. Je te laisse pour cela vérifier que tu es au point avec le théorème de la bijection ou d’autres théorèmes essentiels, comme celui des valeurs intermédiaires.
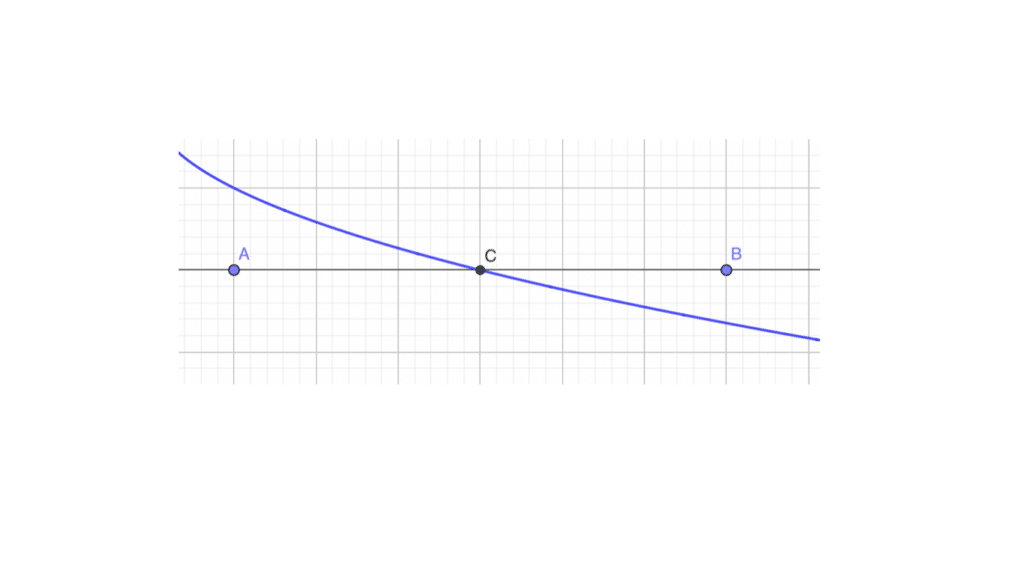
Supposons par la suite que l’on cherche à approcher la solution \(c\) de l’équation et que la fonction \(f\) est strictement monotone sur l’intervalle \([a,b], c\in [f(a),f(b)]\) avec \(f(a)*f(b) < 0.\) On signifie ici que les images de a et de b par \(f\) sont de signes opposés, de sorte que l’on soit certain que \(c\) (que l’on veut approcher) soit dans \([f(a),f(b)].\)
Dans l’extrait graphique ci-dessous, on a bien \(f(A)*f(B)<0.\) Ainsi, tu respectes les conditions et tu peux commencer à aborder le principe de dichotomie.
Tu sais que la solution est \(c \in [a,b].\) Tu vas alors créer une dernière variable qui va te permettre d’approcher avec la précision \(\epsilon\) que tu choisis, cette dernière variable sera ici nommée \(m\) telle que \(m = \frac{a+b}{2}.\) C’est ici que le principe de substitution va te permettre d’approcher la solution \(c\).
L’algorithme
Voici donc l’algorithme de dichotomie. Comme tu peux le voir, le principe de substitution (symbolisé par le symbole \(=\)) joue un rôle majeur. On le voit notamment aux lignes 3, 5 et 7. Comme expliqué plus haut, la première étape est de donner en paramètre de la fonction la précision \(\epsilon\) que tu désires. Par la suite, tu entres dans ta boucle while qui va tout faire marcher !
Je te conseille de relire cet article si tu as des doutes sur le principe des boucles en Python.
La boucle for va nous permettre de créer l’intervalle \([c-\epsilon, c+\epsilon]\) en partant de a et b. En fait, à chaque passage dans la boucle, la variable m va déterminer le milieu entre a et b. Après cela, deux cas de figure sont possibles. Le premier, si f(a) et f(m) sont de signes opposés (ligne 4). Dans ce cas, \(b\) est « trop grand » pour approcher \(c\) et donc \(m\) « prend la place » de \(b\) (ligne 5). Dans l’autre cas, si \(f(m)\) et \(f(a)\) sont du même signe, alors a est « trop petit » pour approcher \(c\) et donc m prend la place de a.
C’est donc ainsi de suite que la boucle for va nous permettre d’atteindre notre objectif d’approximation. Une fois que tu remplis la condition placée dans le if, soit que la différence entre \(a\) et \(b\) est strictement inférieure à \(\epsilon\), alors Python renvoie la valeur finale de m. L’algorithme permet au final d’obtenir la valeur moyenne entre \([c-\epsilon\) et \(c+\epsilon]\).
Un cas pratique
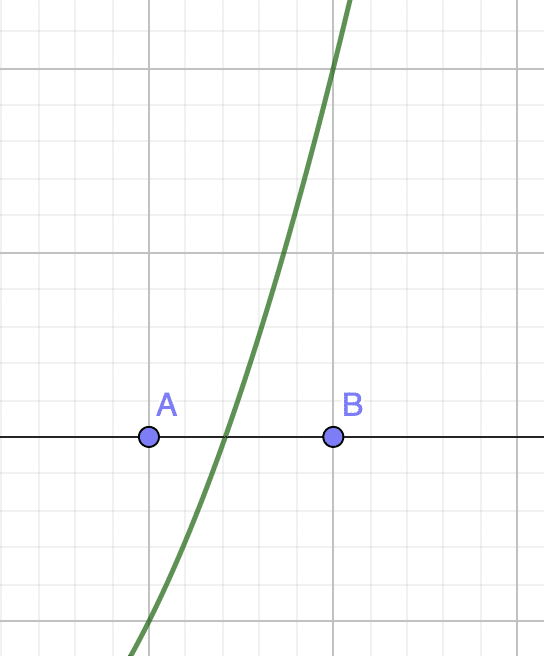
Dans cet exemple, tu verras comment approcher \(\sqrt{2}\) avec cette méthode. On va donc prendre la fonction \(f : x \mapsto x^2-2\) sur \(\mathbb{R}^{+}\) et résoudre l’équation \(f(x) = 0\).
Tu commences par coder ta fonction, ce qui te donne :
On fixe donc \(a = 0\) et \(b=2\). Avec cela, tu as bien \(f(a)*f(b) < 0\) et tu peux donc approcher la solution de l’équation. Tu insères alors les valeurs dans l’algorithme en entrant dichotomie (0,2,10**(-3)). L’algorithme te renvoie 1,4150390625, ce qui est bien une approximation de la célèbre valeur de \(\sqrt{2}\). Tu remarqueras d’ailleurs que plus la précision est petite, plus l’approximation est bonne !
Conclusion
L’algorithme de dichotomie représente un outil puissant pour résoudre des équations de la forme \(f(x) = 0\) de manière efficace, surtout lorsqu’il est implémenté en Python. Ce type d’algorithme est non seulement fondamental pour comprendre les principes de base de la programmation en mathématiques, mais il est également récurrent dans les sujets de concours, notamment depuis l’intégration du Python dans les programmes des prépas ECG et ECT.
Maîtriser cet algorithme te permettra non seulement de t’approcher au plus près de solutions précises, mais aussi de te préparer efficacement aux exigences des épreuves de concours. N’hésite pas à pratiquer en résolvant divers problèmes, car c’est en s’exerçant que l’on acquiert une maîtrise solide des concepts.
Même si python n’est au programme que depuis 2023, l’algorithme de dichotomie est déjà tombé au concours !
Tu peux retrouver de manière plus générale tous les articles de maths ici !