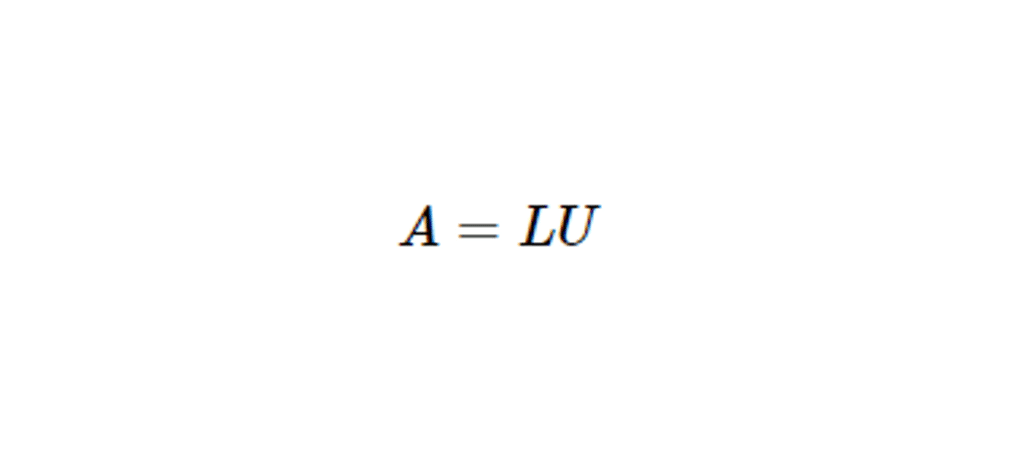La décomposition LU est une technique fondamentale de l’algèbre linéaire, largement utilisée pour simplifier la résolution de systèmes d’équations linéaires, le calcul de déterminants, et bien d’autres opérations matricielles complexes. Elle se révèle particulièrement précieuse en classe préparatoire, où la maîtrise des matrices et des algorithmes associés est cruciale pour réussir les concours. Cet article se propose de te guider à travers les principes mathématiques de la décomposition LU, en abordant sa définition, les conditions de son existence et l’algorithme permettant de la mettre en œuvre, le tout accompagné d’exemples concrets pour une meilleure compréhension. En te concentrant sur ces aspects, tu renforceras tes compétences en manipulation matricielle, une aptitude indispensable pour les épreuves de mathématiques. Ainsi, bien que cette notion soit hors programme, une compréhension approfondie de cette dernière est un bon moyen de se préparer à l’épreuve du Maths I et aux oraux de mathématiques.
Définition et principe de la décomposition LU
La décomposition LU consiste à écrire une matrice carrée \( A \) de taille \( n \times n \) comme le produit de deux matrices : une matrice triangulaire inférieure \( L \) et une matrice triangulaire supérieure \( U \). Formellement, cela s’écrit :
\[
A = LU
\]
où :
- \( L \) (comme Lower) est une matrice triangulaire inférieure avec des 1 sur la diagonale (dans le cas de la décomposition LU sans pivotage) ;
- \( U \) (comme Upper) est une matrice triangulaire supérieure.
Cette décomposition LU pourra grandement t’aider à résoudre certains exercices d’algèbre linéaire, où une compréhension approfondie des matrices est cruciale.
Conditions pour l’existence de la décomposition LU
Pour qu’une matrice \( A \) admette une décomposition LU sans pivotage, il faut que tous ses premiers mineurs principaux soient non nuls. Autrement dit, pour tout \( k \) allant de 1 à \( n \), le déterminant de la sous-matrice \( A_k \) (de dimension \( k \times k \)) doit être non nul. Ou encore, la sous-matrice \( A_k \) doit être inversible.
Si cette condition n’est pas remplie, la décomposition LU existe tout de même, mais elle nécessite un pivotage, ce qui implique une réorganisation des lignes (ou des colonnes) de la matrice \( A \).
Algorithme de décomposition LU
L’algorithme pour obtenir les matrices \( L \) et \( U \) à partir d’une matrice \( A \) est basé sur des opérations élémentaires sur les lignes. Voici les étapes générales.
1. Initialisation : commence par poser \( L \) comme la matrice identité de taille \( n \) et \( U \) comme une copie de la matrice \( A \).
2. Élimination de Gauss : pour chaque colonne \( j \), à partir de la première jusqu’à la \( n \)-ième, soustrais de la \( i \)-ième ligne un multiple de la \( j \)-ième ligne pour annuler les éléments en dessous de la diagonale dans la colonne \( j \). Le facteur multiplicatif utilisé pour cette opération sera stocké dans \( L_{ij} \).
3. Mise à jour de \( U \) : la matrice \( U \) est modifiée à chaque étape de sorte qu’à la fin du processus, elle devient une matrice triangulaire supérieure.
4. Finalisation : après avoir effectué ces opérations pour toutes les colonnes, tu obtiens \( L \) comme une matrice triangulaire inférieure et \( U \) comme une matrice triangulaire supérieure telles que \( A = LU. \)
Exemple de décomposition LU
Prenons un exemple simple pour illustrer la décomposition LU. Soit la matrice suivante :
\[
A = \begin{pmatrix}
2 & 3 & 1 \\
4 & 7 & 3 \\
4 & 7 & 4
\end{pmatrix}
\]
Nous voulons la décomposer en \( LU \).
Étape 1 : Initialisation
\[
L = \begin{pmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}, \quad U = \begin{pmatrix}
2 & 3 & 1 \\
4 & 7 & 3 \\
4 & 7 & 4
\end{pmatrix}
\]
Étape 2 : Élimination de Gauss
Pour annuler les éléments en dessous de \( U_{11} \), on effectue les opérations suivantes :
– Pour la deuxième ligne : \( \displaystyle L_{21} = \frac{4}{2} = 2 \), on soustrait deux fois la première ligne de la deuxième ligne de \( U \).
\[
U = \begin{pmatrix}
2 & 3 & 1 \\
0 & 1 & 1 \\
4 & 7 & 4
\end{pmatrix}, \quad L = \begin{pmatrix}
1 & 0 & 0 \\
2 & 1 & 0 \\
0 & 0 & 1
\end{pmatrix}
\]
– Pour la troisième ligne : \( L_{31} = \frac{4}{2} = 2 \), on soustrait deux fois la première ligne de la troisième ligne de \( U \).
\[
U = \begin{pmatrix}
2 & 3 & 1 \\
0 & 1 & 1 \\
0 & 1 & 2
\end{pmatrix}, \quad L = \begin{pmatrix}
1 & 0 & 0 \\
2 & 1 & 0 \\
2 & 0 & 1
\end{pmatrix}
\]
Ensuite, on annule \( U_{32} \) en soustrayant la deuxième ligne de la troisième ligne. Le facteur est \( L_{32} = \frac{1}{1} = 1 \).
\[
U = \begin{pmatrix}
2 & 3 & 1 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{pmatrix}, \quad L = \begin{pmatrix}
1 & 0 & 0 \\
2 & 1 & 0 \\
2 & 1 & 1
\end{pmatrix}
\]
Ainsi, nous avons :
\[
A = \begin{pmatrix}
2 & 3 & 1 \\
4 & 7 & 3 \\
4 & 7 & 4
\end{pmatrix} = \begin{pmatrix}
1 & 0 & 0 \\
2 & 1 & 0 \\
2 & 1 & 1
\end{pmatrix} \times \begin{pmatrix}
2 & 3 & 1 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{pmatrix}
\]
Tu peux retrouver un exemple de décomposition LU dans la notion de matrices de Fibonacci, issues de la célèbre suite de Fibonacci.
Résolution des systèmes linéaires avec la décomposition LU
Une des applications principales de la décomposition LU en classe préparatoire est la résolution de systèmes linéaires. Supposons que l’on ait un système \( A \mathbf{x} = \mathbf{b} \). Si l’on connaît la décomposition LU de \( A \), on peut résoudre ce système en deux étapes :
1. Résolution de \( L \mathbf{y} = \mathbf{b} \) : en utilisant la matrice \( L \), on résout ce système par substitution avant.
2. Résolution de \( U \mathbf{x} = \mathbf{y} \) : ensuite, on résout ce système par substitution arrière, utilisant la matrice \( U \).
Ce processus est efficace, car il évite la nécessité de recalculer des inverses de matrices, ce qui est particulièrement avantageux pour les matrices de grande taille.
Le cas symétrique
Lorsque la matrice \( A \) est symétrique, c’est-à-dire que \( A = A^T \), la décomposition LU classique peut être adaptée pour exploiter cette symétrie. Dans ce cas, \( A \) peut être décomposée sous la forme \( A = LDL^T \), où :
- \( L \) est une matrice triangulaire inférieure ;
- \( D \) est une matrice diagonale ;
- \( L^T \) est la transposée de \( L \).
Cette décomposition, parfois appelée décomposition de Crout, est une version spécialisée de la décomposition LU, particulièrement utile pour les matrices symétriques. Elle conserve la structure triangulaire inférieure de \( L \), tout en simplifiant la matrice \( U \) en une matrice diagonale \( D \).
Lorsque \( A \) est en plus définie positive, la décomposition peut être simplifiée davantage par la méthode de Cholesky. Ici, \( A \) se factorise sous la forme \( A = LL^T \), où :
- \( L \) est une matrice triangulaire inférieure avec des éléments diagonaux strictement positifs ;
- \( L^T \) est la transposée de \( L \).
La décomposition de Cholesky peut être considérée comme un cas particulier de la décomposition LU, offrant une solution plus rapide et plus stable pour les matrices symétriques définies positives. Ces variantes montrent comment la décomposition LU peut être adaptée et simplifiée en fonction des propriétés spécifiques de la matrice étudiée.
Conclusion
La décomposition LU est une technique puissante en algèbre linéaire, essentielle pour résoudre les systèmes linéaires et faciliter les calculs matriciels en général. En classe préparatoire, maîtriser cette méthode est indispensable pour aborder les épreuves de mathématiques avec confiance. La pratique régulière de la décomposition LU sur divers types de matrices te permettra de l’intégrer pleinement et de l’appliquer efficacement le jour du concours.
Pour t’entraîner à manipuler des matrices, tu peux réaliser les sujets suivants : EML 2022 et Maths I 2016 (mathématiques approfondies).
Tu peux retrouver le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder à toutes nos autres ressources mathématiques !