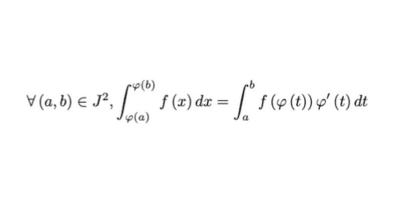Dans la plupart des sujets de concours, tu devras calculer des intégrales en effectuant un changement de variable. Les règles de Bioche peuvent être utiles pour poser le bon changement dans certains cas.
Changement de variable vu en SUP
L’énoncé vu en cours de mathématiques en SUP est le suivant :
Soient \(I \) et \(J \) deux intervalles de \( \mathbb{R} \), \( f \in C ^{ 0 } \left( I, \mathbb{C} \right) \) et \( \varphi \in C ^{ 1 } \left( J,I \right) \).
Alors :
\[ \forall \left( a,b \right) \in J ^{ 2 } , \displaystyle \int _{ \varphi \left( a \right) } ^{ \varphi \left( b \right) } f \left( x \right) dx = \int _{ a } ^{ b } f \left( \varphi \left( t \right) \right) \varphi ‘ \left( t \right) dt \]
Cette relation peut se lire dans les deux sens.
Méthode pour faire un changement de variable
On pose la fonction \(x= \varphi \left( t \right) \) et on vérifie que \(\varphi\) est de classe \( C ^{ 1 } \) entre \(a\) et \(b\).
On différencie la relation précédente : \(dx= \varphi ‘ \left( t \right) dt \).
On remplace \( f \left( x \right) dx \) par \(f \left( \varphi \left( t \right) \right) \varphi ^{ ‘ } \left( t \right) dt \).
On change les bornes : quand \(x\) varie entre \( \varphi \left( a \right) \) et \( \varphi \left( b \right) \), \(t\) varie entre \(a\) et \(b\).
Exemples de changement de variable
Exemple 1 : sens direct
Calculer l’intégrale : \( I= \displaystyle \int _{ 1 } ^{ 4 } \frac { dx } { 1+ \sqrt{ x } } = \int _{ 1 ^2 } ^{ 2 ^2 } \frac { 1 } { 1+ \sqrt{ x } } dx \).
On pose le changement de variable suivant : \( x= t^2 = \varphi \left( t \right) \).
On a bien \(\varphi \) de classe \(C ^{ 1 } \) entre 1 et 2.
Ce qui nous donne : \( dx=\displaystyle 2tdt \).
Dès lors : \( I=\displaystyle \int _{ 1 } ^{ 2 } \frac { 2t } { 1+t } dt=2 \int _{ 1 } ^{ 2 } \frac { t } { 1+t } dt \)
Or : \(\displaystyle \int _{ 1 } ^{ 2 } \frac { t } { 1+t } dt= \int _{ 1 } ^{ 2 } \frac { t+1-1 } { 1+t } dt= \int _{ 1 } ^{ 2 } (1- \frac { 1 } { 1+t })dt \)
Ensuite, tu dois normalement être capable de déterminer la primitive.
Exemple 2 : sens indirect
Calculer l’intégrale : \(J=\displaystyle \int _{ 0 } ^{ 1 } \frac { e ^{ 2t } } { 1+e ^{ t } } dt \)
On peut réécrire l’intégrale précédente sous cette forme : \( J=\displaystyle \int _{ 0 } ^{ 1 } \frac { e ^{ t } } { 1+e ^{ t } } e ^{ t } dt \)
À l’intérieur de l’intégrale, on a quelque chose du type : \( f \left( \varphi \right) \varphi ‘ \) avec \( \begin{cases} f \left( y \right) =\displaystyle \frac { y } { 1+y } \\ \varphi = \exp\vphantom{1} \end{cases} \)
Donc : \( J=\displaystyle \int _{ e ^{ 0 } } ^{ e ^{ 1 } } \frac { y } { 1+y } dy \).
Il ne te reste plus qu’à utiliser la méthode classique du \(+1-1\) et c’est terminé.
Changement de variable vu en SPE
L’énoncé vu en cours de mathématiques en SPE est le suivant :
Soient \(a,b, \alpha , \beta \) dans \( \bar{ \mathbb{R} } \) tels que \( a<b \) et \( \alpha<\beta \).
Soit \( \varphi : ] \alpha , \beta [ \to ] a,b [ \) une bijection strictement croissante de classe \( C ^{ 1 } \). Soit \(f: ] a , b [ \to \mathbb{ K } \) une fonction continue par morceaux.
Les deux intégrales \(\displaystyle \int _{ a } ^{ b } f \left( t \right) dt \) et \( \displaystyle \int _{ \alpha } ^{ \beta } f \left( \varphi \left( u \right) \right) \varphi ‘ \left( u \right) du \) sont de même nature et dans le cas où elles convergent, elles sont égales.
Exemple : intégrale impropre
Calculer l’intégrale : \( I= \displaystyle \int _{ 0 } ^{ + \infty } \frac { e ^{ -x } } { \sqrt{ x } } dx \)
Première étape : on s’assure que l’intégrale converge en examinant son comportement en \(0\) et \( + \infty\).
On pose le changement de variable : \( x= t^2 \), qui vérifie bien les hypothèses du théorème précédent.
Quand on différencie la relation précédente, on obtient : \( dx= 2t dt \)
Concernant les bornes, quand \(x=0\) alors \(t=0\), et quand \(x=+ \infty\) on a \(t=+ \infty\)
Donc : \( I= \displaystyle \int _{ 0 } ^{ + \infty } \frac { e ^{ -t ^2 } } { t } 2t dt=2 \int _{ 0 } ^{ + \infty } e ^{ -t ^2 } dt=2 \frac { \sqrt{ \pi } } { 2 } = \sqrt{ \pi } \)
Les règles de Bioche
On considère \(f(x)\) une fraction rationnelle en \(cos(x), sin(x)\) et \(tan(x)\).
Pour calculer l’intégrale \( \displaystyle \int _{ a } ^{ b } f \left( x \right) dx \) et la transformer en fraction rationnelle en \(u\), on peut poser des changements de variable en fonction de l’invariance de \( w \left( x \right) =f \left( x \right) dx \).
- Premier cas : si \( w \left( -x \right) =w \left( x \right) \) alors on pose \( u= \cos \left( x \right) \)
- Deuxième cas : si \( w \left( \pi -x \right) =w \left( x \right) \) alors on pose \( u= \sin \left( x \right) \)
- Troisième cas : si \( w \left( \pi +x \right) =w \left( x \right) \) alors on pose \( u= \tan \left( x \right) \)
Application des règles de Bioche
Exemple 1
Calculer l’intégrale : \(I=\displaystyle \int _{ \frac{\sqrt{\pi}}{4} } ^{ \frac{\sqrt{\pi}}{2} } \frac { \sin \left( x \right) } { 3+ \cos ^{ 2 } \left( x \right) } dx \)
On pose : \( w (x) = \displaystyle \frac { \sin \left( x \right) } { 3+ \cos ^{ 2 } \left( x \right) } dx \)
Et on remarque que \(w(x)=w(-x)\), dès lors on pose donc le changement de variable : \( u= \cos \left( x \right) \)
Ce qui nous donne : \(du=- \sin \left( x \right) dx \)
Ainsi, quand \(x\) varie entre \({ \displaystyle \frac{\sqrt{\pi}}{4} }\) et \({ \displaystyle \frac{\sqrt{\pi}}{2} }\), \(u\) varie entre \({ \displaystyle \frac{\sqrt{2}}{2} }\) et \(0\).
Donc : \( I= \displaystyle \int _{ \frac { \sqrt{ 2 } } { 2 } } ^{ 0 } \frac { -du } { 3+u ^{ 2 } } \)
On peut factoriser par 3 au dénominateur : \( I=- \displaystyle \int _{ \frac { \sqrt{ 2 } } { 2 } } ^{ 0 } \frac { du } { 3 \left( 1+ \frac { u ^{ 2 } } { 3 } \right) } \)
On obtient ainsi : \( I= \displaystyle \frac { -1 } { 3 } \int _{ \frac { \sqrt{ 2 } } { 2 } } ^{ 0 } \frac { \frac { 1 } { \sqrt{ 3 } } \sqrt{ 3 } } { 1+ \left( \frac { u } { \sqrt{ 3 } } \right) ^{ 2 } } du= \frac { \sqrt{ 3 } } { 3 } \int _{ 0 } ^{ \frac { \sqrt{ 2 } } { 2 } } \frac { \frac { 1 } { \sqrt{ 3 } } } { 1+ \left( \frac { u } { \sqrt{ 3 } } \right) ^2 } du \)
C’est presque terminé !
\( I= \displaystyle \frac { \sqrt{ 3 } } { 3 } \left[ arc \tan \left( \frac { u } { \sqrt{ 3 } } \right) \right] ^{ \frac { \sqrt{ 2 } } { 2 } } _{ 0 } = \frac { \sqrt{ 3 } } { 3 } \left( arc \tan \left( \frac { \frac { \sqrt{ 2 } } { 2 } } { \sqrt{ 3 } } \right) -arc \tan \left( \frac { 0 } { \sqrt{ 3 } } \right) \right) = \frac { \sqrt{ 3 } } { 3 } arc \tan \left( \frac { \sqrt{ 6} } { 6 } \right) \)
Exemple 2
Calculer l’intégrale : \( I= \displaystyle \int _{ 0 } ^{ \frac { \pi } { 4 } } \frac { \sin \left( x \right) } { \sin \left( x \right) + \cos \left( x \right) } dx \)
On note : \(w \left( x \right) = \frac { \sin \left( x \right) } { \cos \left( x \right) + \sin \left( x \right) } dx \)
On remarque qu’on a \( w \left( x+ \pi \right) =w \left( x \right) \), on fait donc le changement de variable \(t= \tan \left( x \right)\).
On différencie la relation suivante : \(dt= \left( 1+ \tan ^2 \left( x \right) \right) dx= \left( 1+t ^2 \right) dx \)
Ainsi, quand \(x\) varie entre \(0\) et \( \frac { \pi } { 4 } \), \(t\) varie entre \( \tan \left( 0 \right) =0 \) et \( \tan \left( \frac { \pi } { 4 } \right) =1 \)
On fait donc : \( I= \displaystyle \int _{ 0 } ^{ \frac { \pi } { 4 } } \frac { \sin \left( x \right) } { \cos \left( x \right) + \sin \left( x \right) } dx= \int _{ 0 } ^{ \frac { \pi } { 4 } } \frac { \sin \left( x \right) } { \sin \left( x \right) \left( 1+ \frac { \cos \left( x \right) } { \sin \left( x \right) } \right) } dx= \int _{ 0 } ^{ \frac { \pi } { 4 } } \frac { 1 } { 1+ \frac { \cos \left( x \right) } { \sin \left( x \right) } } dx = \int _{ 0 } ^{ \frac { \pi } { 4 } } \frac { 1 } { 1+ \frac { 1 } { \tan \left( x \right) } } dx \)
Ce qui nous donne : \( I= \displaystyle \int _{ 0 } ^{ 1 } \frac { 1 } { 1+ \frac { 1 } { t } } \frac { dt } { 1+t ^2 } \)
En effectuant une décomposition en éléments simples, on peut obtenir le résultat final.
Lire aussi : Neuf astuces sur les intégrales