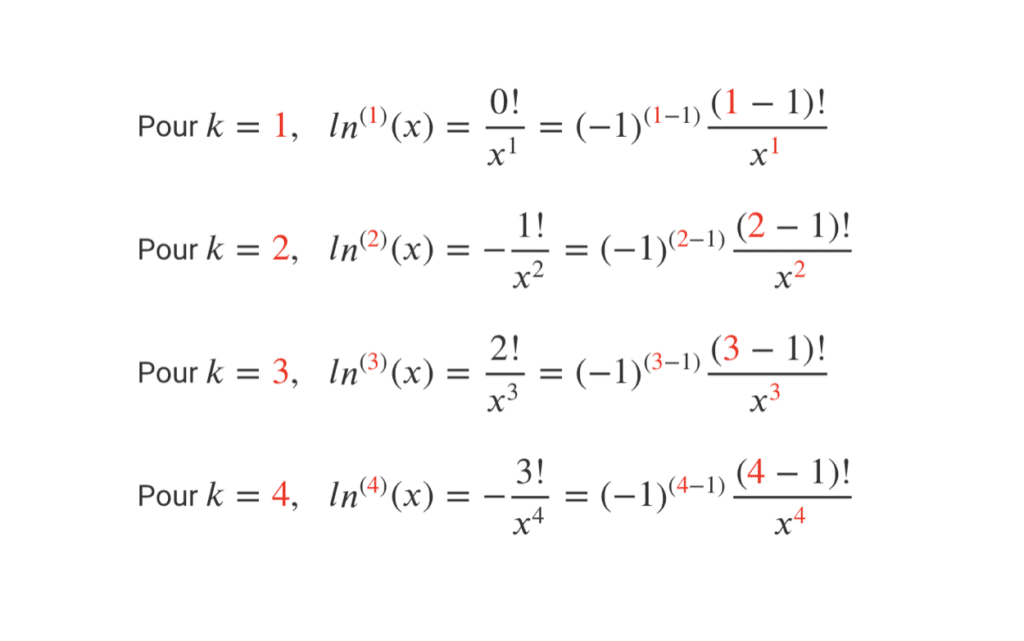Cet article te propose une méthode détaillée pour apprendre à faire tes itérations pas à pas. Tu ne trouveras nulle part ailleurs une méthode aussi détaillée et complète, même dans les cours de ton prof. En fait, cette méthode, tout le monde l’utilise implicitement, mais personne n’a jamais pris la peine de l’expliquer de façon aussi détaillée.
Je te présente trois exemples différents montrant les différents types d’itérations. Avec tout cela, tu seras capable de faire n’importe quelle itération !
Dédicace à Agathe pour cet article.
Qu’est-ce qu’une itération ?
L’itération est l’action de répéter un processus. En maths, on parle d’itération lorsque l’on écrit une expression dépendant d’une variable \(n\). On dira qu’elle est écrite au rang \(n\) à plusieurs rangs successifs.
Les itérations peuvent se faire en augmentant de rang un à un (\(0, 1, 2, 3, 4, \dots\)) ou en baissant de rang un à un (\(n, (n-1), (n-2), (n-3), \dots\)).
Les itérations peuvent être finies (lorsque l’on augmente les rangs 0 jusqu’à \(n\) par exemple
(\(0, 1, 2, 3, 4, \dots, n\)).
Mais elles peuvent également être infinies (lorsque l’on augmente les rangs 0 jusqu’à un rang infini par exemple (\(0, 1, 2, 3, 4, \dots\)).
De fait, la méthode d’itération va légèrement différer en fonction.
Contexte dans lequel itérer
L’itération se fera quasi systématiquement lorsque l’énoncé te demande d’exprimer une expression de \(A_n\) en fonction de \(n\) par exemple. Donc, lorsque c’est à nous de trouver une expression.
La subtilité dans le raisonnement par itération est qu’il ne doit pas apparaître sur ta copie, car il n’est pas considéré comme rigoureux. Mais il est pourtant indispensable de le faire pour conjecturer une relation ! Le raisonnement est donc entièrement à faire au brouillon. Une fois que tu auras dégagé une conjecture, tu pourras passer à la rédaction sur ta copie et la montrer par récurrence.
En montrant ta conjecture par récurrence, le correcteur comprendra le raisonnement que tu as fait au brouillon avec tes itérations. Mais la réponse à la question sera présentée de manière rigoureuse sur ta copie.
Qu’est-ce qu’une conjecture ?
Une conjecture est une proposition mathématique pour laquelle on ne connaît pas encore de démonstration, mais que l’on croit fortement être vraie. Lorsque l’on dégage une conjecture à l’aide d’un raisonnement par itération, il est indispensable de la démontrer par récurrence, comme expliqué précédemment. De ce fait, la proposition mathématique ne sera plus une conjecture, mais une relation mathématique vérifiée.
Conjecture à partir d’une relation de récurrence (itération finie) – difficulté assez faible
Soit \(a \in \mathbb R\) et soit \((I_n)_{n \in \mathbb N}\) la suite définie par :
\(\displaystyle \forall n \in \mathbb N, I_{\color{green}{n+1}}=\frac{n+1}{a} I_{\color{blue}n}\)
On rappelle que cette relation est appelée relation de récurrence, car on observe un décalage de 1 rang entre \(\color{blue}n\) et \({\color{green}{n+1}}\)
On veut déterminer une expression de \(I_n\) en fonction de \(n\) pour tout \(n \in \mathbb N\). Pour cela, on va se servir de la relation de récurrence de l’énoncé comme base de notre itération.
Étape 1
Il suffit de repérer que sur le membre de gauche, on a \(I_{\color{green}{n+1}}\) (donc, la suite est écrite au rang \({\color{green}{n+1}}\)) et sur le membre de droite, on a \(I_{\color{blue}n}\) (donc, la suite est écrite au rang \(\color{blue}n\)). La méthode d’itération va consister à baisser d’un rang toute l’expression (et voir la nouvelle expression qu’on obtient), puis d’un autre rang, puis encore d’un autre… jusqu’à ne plus pouvoir baisser d’un rang.
Je te conseille fortement d’être très organisé·e et très minutieux·se sur ton brouillon lorsque tu itères. Tu vas te rendre compte que c’est beaucoup plus simple de voir ce qu’il se passe ensuite !
Afin de s’organiser dans son itération, on va nommer le rang \(k\), et on va dire à quel rang est égal \(k\) à chaque fois qu’on écrit l’expression à un nouveau rang. Par exemple, lorsque l’on écrit l’expression au rang \(n\) (donc, au rang \(k=n\)), on écrira ce qui suit (sur une seule ligne) :
Pour \(\displaystyle k=n, \; \; I_{n}=\frac{n}{a}I_{n-1}\)
En général, il y aura le rang \(n+1\) dans la relation de récurrence, mais pour notre itération, on préférera commencer au rang \(n\).
Ensuite, on va continuer d’écrire les expressions à tous les rangs en les alignant les unes sous les autres, de cette façon :
Pour \(\displaystyle k=n, \; \; I_{n}=\frac{n}{a} I_{n-1}\)
Pour \(\displaystyle k=n-1, \; \; I_{n-1}=\frac{n-1}{a} I_{n-2}\)
Pour \(\displaystyle k=n-2, \; \; I_{n-2}=\frac{n-2}{a} I_{n-3}\)
…
Et on baisse d’un rang, et encore d’un autre… mais au bout d’un moment, il faut s’arrêter. Comment savoir à quel rang s’arrêter ?
En fait, cela dépend de comment est définie la suite. Par exemple, ici, la suite est définie sur \(\mathbb N\). Donc, on sait que le dernier rang de la suite sera \(0\) (donc, le terme \(I_0\) est bien le premier terme de cette suite).
De fait, elle devra s’arrêter à \(I_0\). On peut donc penser intuitivement à s’arrêter au rang \(k=0\), sauf que, attention, si tel était le cas, on aurait :
Pour \(\displaystyle k=0, \; \; I_{0}=\frac{0}{a} I_{\color{red}{-1}}\)
Ce qui ne va pas du tout ! On remarque que l’on a du \(I_{\color{red}{-1}}\), ce qui n’est pas possible car la suite n’est pas définie sur \(\mathbb Z\). Le premier terme est à \(I_0\), donc on est obligés de terminer au rang \(k=1\) et non \(k=0\)
Pour \(\displaystyle k=1, \; \; I_{1}=\frac{1}{a} I_{0}\)
Ainsi, si on reprend nos expressions alignées les unes sous les autres :
Pour \(\displaystyle k=n, \; \; I_{n}=\frac{n}{a} I_{n-1}\)
Pour \(\displaystyle k=n-1, \; \; I_{n-1}=\frac{n-1}{a} I_{n-2}\)
Pour \(\displaystyle k=n-2, \; \; I_{n-2}=\frac{n-2}{a} I_{n-3}\)
…
Pour \(\displaystyle k=2, \; \; I_{2}=\frac{2}{a} I_{1}\)
Pour \(\displaystyle k=1, \; \; I_{1}=\frac{1}{a} I_{0}\)
N.B. : Astuce importante
Tu auras remarqué que j’ai écrit les trois premières expressions et les deux dernières entre les « … ».
Je te conseille vivement de faire ceci à chaque fois que tu rencontres des « … », afin de bien comprendre l’itération qui va se mettre en place. En effet, écrire la première expression et la dernière entre les « … » est parfois insuffisant pour appréhender ton itération.
Étape 2
Cette étape va consister à « assembler » toutes les expressions à la suite pour ne former qu’une seule et même expression. Si tu as bien effectué l’étape 1, normalement, toutes les expressions ont un point commun pour être regroupées.
On a donc :
\(\displaystyle I_{n}=\frac{n}{a} I_{n-1}\), or \(\displaystyle \color{blue}{I_{n-1}=\frac{n-1}{a} I_{n-2}}\), donc :
\(\displaystyle I_{n}=\frac{n}{a} \color{blue}{(\frac{n-1}{a} I_{n-2})}\), or \(\displaystyle \color{blue}{I_{n-2}=\frac{n-2}{a} I_{n-3}}\), donc :
\(\displaystyle I_{n}=\frac{n}{a} \frac{n-1}{a} \color{blue}{(\frac{n-2}{a} I_{n-3})}\)
…
\(\displaystyle I_{n}=\frac{n}{a} \frac{n-1}{a} \frac{n-2}{a} \dots \frac{3}{a}\color{blue}{(\frac{2}{a} I_1)}\), or \(\displaystyle \color{blue}{I_{1}=\frac{1}{a} I_{0}}\), donc :
\(\displaystyle I_{n}=\frac{n}{a} \frac{n-1}{a} \frac{n-2}{a} \dots \frac{2}{a} \color{blue}{(\frac{1}{a}I_0)}\)
Maintenant, au numérateur, il faut se demander comment simplifier \(n \times (n-1) \times (n-2) \times \dots \times 2 \times 1\)
On reconnaît donc que \(n \times (n-1) \times (n-2) \times \dots \times 2 \times 1=n!\)
Et au dénominateur, il faut se demander comment simplifier \(a \times a \times a \times \dots \times a \times a\)
Pour cela, il suffit de compter le nombre de \(a\). C’est très simple, on compte le nombre de rangs que l’on a utilisé dans les expressions en étape 1. On a commencé au rang \(k=n\) et terminé au rang \(k=1\), donc : \(n-1+1=n\)
Donc : \(a \times a \times a \times \dots \times a \times a=a^n\)
Étape 3
On obtient donc notre conjecture :
\(\displaystyle I_{k}=\frac{k!}{a^k}I_0\)
L’itération comportant un nombre fini de termes, on écrit les expressions des rangs allant de \(0\) à \(n\), la relation est donc vraie sur :
\(\displaystyle \forall k \in \color{red}{[\![0,n]\!]}, I_{k}=\frac{k!}{a^k}I_0\)
L’étape 3 va alors consister à la montrer par récurrence sur ta copie, proprement. On rappelle que les étapes 1 et 2 doivent impérativement se faire au brouillon et seulement au brouillon.
Sauf qu’il s’agit d’une récurrence finie, qu’on appelle plus rigoureusement une montée finie. Le début de la réponse à la question initiale s’écrit donc sur ta copie :
« Soit \(n \in \mathbb N\)
Montrons par montée finie que : \(\displaystyle \forall k \in [\![0,n]\!], I_{k}=\frac{k!}{a^k}I_0\) »
En écrivant ceci, le correcteur va tout de suite voir si tu as bien réfléchi au brouillon, car il saura instantanément si tu as la bonne conjecture ou non. Puis, il verra ton raisonnement au cours de ta récurrence/montée finie. À toi de jouer !
Puis, on conclut pour le terme en \(k=n\), puisque l’énoncé nous a demandé cette relation pour tout \(n \in \mathbb N\)
Ainsi,
\[\fbox{\(\displaystyle \forall n \in \mathbb N, I_{n}=\frac{n!}{a^n}I_0\)}\]
N.B. : Il aurait également été possible (pour gagner du temps) de passer par une récurrence directement. En effet, ce contexte est faisable lorsque l’énoncé demande la relation pour tout \(n \in \mathbb N\) et que la variable \(n\) n’est pas fixée par l’énoncé lui-même !
« Montrons par récurrence que : \(\displaystyle \forall n \in \mathbb N, I_{n}=\frac{n!}{a^n}I_0\) »
Conjecture de difficulté intermédiaire (itération infinie)
Déterminer la dérivée \(n\)ième de la fonction \(\ln\) pour \(n \in \mathbb N\). Voilà une itération qui se complique un peu.
Étape 1
Contrairement à l’exemple précédent, on ne va pas descendre de rang, mais monter de rang.
Soit \(x \in \mathbb R^{*}_{+}\)
Pour \(\displaystyle k=0, \; \; ln^{(0)}(x)=\ln(x)\)
Pour \(\displaystyle k=1, \; \; ln^{(1)}(x)=\frac{1}{x}\)
Pour \(\displaystyle k=2, \; \; ln^{(2)}(x)=-\frac{1}{x^2}\)
…
?
Ici, on ne voit pas vraiment d’itération claire se dégager. Notamment car l’expression pour \(k=0\) n’est pas du tout la même que pour les autres rangs, et on n’aperçoit pas trop de lien entre \(k=1\) et \(k=2\).
Dans ce cas, on est invités à continuer l’itération pour quelques rangs encore, jusqu’à trouver un lien.
N.B. : Toujours simplifier au maximum ses calculs.
Pour \(\displaystyle k=0, \; \; ln^{(0)}(x)=\ln(x)\)
Pour \(\displaystyle k=1, \; \; ln^{(1)}(x)=\frac{1}{x}\)
Pour \(\displaystyle k=2, \; \; ln^{(2)}(x)=-\frac{1}{x^2}\)
Pour \(\displaystyle k=3, \; \; ln^{(3)}(x)=\frac{2x}{x^4}=\frac{2}{x^3}\)
Pour \(\displaystyle k=4, \; \; ln^{(4)}(x)=-\frac{6x^2}{x^6}=-\frac{6}{x^4}\)
Pour \(\displaystyle k=5, \; \; ln^{(5)}(x)=\frac{24x^3}{x^8}=\frac{24}{x^5}\)
…
Quelque chose semble se dégager avec l’alternance de signe et la puissance du dénominateur. Cependant, on essaie encore de comprendre ce qu’il se passe au numérateur.
Étape 2
Cette étape va être plus compliquée que dans l’exemple précédent, car il faut réussir à dégager une expression de \(ln^{(n)}\) qui soit claire. Pour ce faire, on va tenter d’exprimer chaque expression en fonction du rang de l’expression.
Par exemple, pour l’expression au rang \(k={\color{red}4}\), le but va être d’exprimer \(\displaystyle ln^{(4)}(x)=-\frac{6}{x^4}\) en fonction de \(\color{red}4\), ce qui donnerait :
Pour \(\displaystyle k={\color{red}4}, \; \; ln^{({\color{red}4})}(x)=(-1)^{\color{red}4}- \frac{6}{x^{\color{red}4}}\)
N.B. : Quelques petites astuces d’itération :
· Lorsque les expressions alternent leur signe entre \(+\) et \(-\) à chaque rang, il faut penser à mettre du \((-1)^n\) (si les expressions des rangs impairs sont négatives) ou du \((-1)^{n\pm 1}\) (si les expressions des rangs pairs sont négatives).
· Lorsque l’on observe une suite de termes qui commence par \((1, 1, 2, 6, 24, \dots )\), il faut penser à du factoriel ! Car \((0!, 1!, 2!, 3!, 4!, \dots)=(1, 1, 2, 6, 24, \dots )\)
Donc, avec ces précisions, on peut écrire :
Pour \(\displaystyle k={\color{red}4}, \; \; ln^{({\color{red}4})}(x)=(-1)^{\color{red}4}- \frac{3!}{x^{\color{red}4}}\), or le \(3!\) ne convient pas vraiment car on souhaiterait l’exprimer en fonction de \({\color{red}4}\). Donc, il suffit tout simplement de remarquer que : \(({\color{red}4}-1)!=3!=6\), et là on a notre \({\color{red}4}\). Donc :
Pour \(\displaystyle k={\color{red}4}, \; \; ln^{({\color{red}4})}(x)=(-1)^{\color{red}4}- \frac{({\color{red}4-1)!}}{x^{\color{red}4}}\)
On peut donc désormais exprimer chaque expression en fonction du rang de l’expression.
Pour \(\displaystyle k={\color{red}0}, \; \; ln^{({\color{red}0})}(x)=\ln(x)\)
Pour \(\displaystyle k={\color{red}1}, \; \; ln^{({\color{red}1})}(x)=\frac{0!}{x^1}=(-1)^{({\color{red}1}-1)}\frac{({\color{red}1}-1)!}{x^{\color{red}1}}\)
Pour \(\displaystyle k={\color{red}2}, \; \; ln^{({\color{red}2})}(x)=-\frac{1!}{x^2}=(-1)^{({\color{red}2}-1)}\frac{({\color{red}2}-1)!}{x^{\color{red}2}}\)
Pour \(\displaystyle k={\color{red}3}, \; \; ln^{({\color{red}3})}(x)=\frac{2!}{x^3}=(-1)^{({\color{red}3}-1)}\frac{({\color{red}3}-1)!}{x^{\color{red}3}}\)
Pour \(\displaystyle k={\color{red}4}, \; \; ln^{({\color{red}4})}(x)=-\frac{3!}{x^4}=(-1)^{({\color{red}4}-1)}\frac{({\color{red}4}-1)!}{x^{\color{red}4}}\)
Pour \(\displaystyle k={\color{red}5}, \; \; ln^{({\color{red}5})}(x)=\frac{4!}{x^5}=(-1)^{({\color{red}5}-1)}\frac{({\color{red}5}-1)!}{x^{\color{red}5}}\)
…
Étape 3
Maintenant, le travail est quasiment terminé ! Il suffit de remplacer le “\(k=\)” dans les expressions. Donc :
Pour \(\displaystyle k={\color{red}0}, \; \; ln^{({\color{red}0})}(x)=\ln(x)\)
Pour \(\displaystyle k={\color{red}1}, \; \; ln^{({\color{red}1})}(x)=(-1)^{({\color{red}1}-1)}\frac{({\color{red}1}-1)!}{x^{\color{red}1}}\)
Pour \(\displaystyle k={\color{red}2}, \; \; ln^{({\color{red}2})}(x)=(-1)^{({\color{red}2}-1)}\frac{({\color{red}2}-1)!}{x^{\color{red}2}}\)
Pour \(\displaystyle k={\color{red}3}, \; \; ln^{({\color{red}3})}(x)=(-1)^{({\color{red}3}-1)}\frac{({\color{red}3}-1)!}{x^{\color{red}3}}\)
Pour \(\displaystyle k={\color{red}4}, \; \; ln^{({\color{red}4})}(x)=(-1)^{({\color{red}4}-1)}\frac{({\color{red}4}-1)!}{x^{\color{red}4}}\)
Pour \(\displaystyle k={\color{red}5}, \; \; ln^{({\color{red}5})}(x)=(-1)^{({\color{red}5}-1)}\frac{({\color{red}5}-1)!}{x^{\color{red}5}}\)
…
\(\fbox{\(\text{Pour} \; \displaystyle k={\color{orange}n}, \; \; ln^{({\color{orange}n})}(x)=(-1)^{({\color{orange}n}-1)}\frac{({\color{orange}n}-1)!}{x^{\color{orange}n}}\)}\)
N.B. : Tu auras remarqué qu’on a enlevé l’expression du terme en \(k=0\), car elle ne rejoint pas le cas général (il ne faudra pas oublier de la rajouter à la fin, on la laisse de côté pour l’instant). Cette conjecture sera donc à montrer sur \(\mathbb N^*\) et non sur \(\mathbb N\)
La rédaction dans ta copie débute donc par :
« Soit \(x \in \mathbb R^*_+\)
Montrons par récurrence que : \(\displaystyle \forall n \in \mathbb N^*, \; ln^{(n)}(x)=(-1)^{(n-1)}\frac{(n-1)!}{x^n}\) »
Lors de la conclusion de la question, ne surtout pas oublier le terme en \(n=0\) qui ne rejoint pas le cas général, il est à distinguer ! Donc, la conclusion ressemble à quelque chose comme :
\[\fbox{\(\displaystyle \forall n \in \mathbb N, \forall x \in \mathbb R^*_+, \ln^{(n)}(x)=
\begin{cases}
(-1)^{(n-1)}\frac{(n-1)!}{x^n} & \text{si} \; n \in \mathbb N^* \\
\ln(x) & \text{si} \; n=0
\end{cases}\)}
\]
Évidemment, c’est le cas seulement si la question est de montrer la dérivée \(n\)ième de \(\ln\) sur \(\mathbb N\) et non sur \(\mathbb N^*\)
Conjecture de difficulté assez élevée (double itération infinie)
Déterminer la puissance \(n\)ième de la matrice \(A=\begin{pmatrix}
0 & 1 & 1 \\
1 & 0 & 0 \\
1 & 0 & 0
\end{pmatrix}\) pour \(n \in \mathbb N\)
Étape 1
Lorsque l’on calcule les puissances \(n\)ième d’une matrice, on calcule toujours ses premiers termes pour émettre une conjecture par itération.
\(A^0=I\)
\(A^1=\begin{pmatrix}
0 & 1 & 1 \\
1 & 0 & 0 \\
1 & 0 & 0
\end{pmatrix}\)
\(A^2=\begin{pmatrix}
2 & 0 & 0 \\
0 & 1 & 1 \\
0 & 1 & 1
\end{pmatrix}\)
\(A^3=\begin{pmatrix}
0 & 2 & 2 \\
2 & 0 & 0 \\
2 & 0 & 0
\end{pmatrix}=2A\)
\(A^4=\begin{pmatrix}
4 & 0 & 0 \\
0 & 2 & 2 \\
0 & 2 & 2
\end{pmatrix}=2A^2\)
On se rend compte qu’il y a une deux suites logiques d’expressions, en fonction de si \(n\) est pair ou impair. Et c’est là que ça se complique. Cela signifie qu’il y aura deux conjectures à faire et donc deux itérations en fonction de si \(n\) est pair ou impair.
Étape 2
Petit récapitulatif, on a les matrices que l’on pourrait nommer de « référence » :
\(A^1=\begin{pmatrix}
0 & 1 & 1 \\
1 & 0 & 0 \\
1 & 0 & 0
\end{pmatrix}\) et \(A^2=\begin{pmatrix}
2 & 0 & 0 \\
0 & 1 & 1 \\
0 & 1 & 1
\end{pmatrix}\), puis :
Pour \(k=0, \; \; A^0=I\)
Pour \(k=1, \; \; A^1=A\)
Pour \(k=2, \; \; A^2=A^2\)
Pour \(k=3, \; \; A^3=2A\)
Pour \(k=4, \; \; A^4=2A^2\)
Puis, on imagine (on conjecture) la suite :
Pour \(k=5, \; \; A^5=A.A^4=A.2A^2=2A^3=4A\)
Pour \(k=6, \; \; A^6=A.A^5=A.4A=4A^2\)
…
Mais maintenant, notre souhait est d’exprimer chaque expression en fonction du rang de l’expression. Sauf que, comme les expressions sont différentes en fonction de si \(n\) est pair ou impair, ça complique les choses.
L’idée à avoir est directement d’exprimer la puissance de la matrice sous la forme de la définition d’un terme pair ou impair, ce qui donnerait :
\(1=2 \times 0+1\)
\(3=2 \times 1+1\)
\(5=2 \times 2+1\)
…
et d’autre part :
\(0=2 \times 0\)
\(2=2 \times 1\)
\(4=2 \times 2\)
\(6=2 \times 3\)
Donc, en reprenant nos expressions :
Pour \(k=0, \; \; A^{2 \times 0}=I\)
Pour \(k=1, \; \; A^{2 \times 0+1}=A\)
Pour \(k=2, \; \; A^{2 \times 1}=A^2\)
Pour \(k=3, \; \; A^{2 \times 1+1}=2A\)
Pour \(k=4, \; \; A^{2 \times 2}=2A^2\)
Pour \(k=5, \; \; A^{2 \times 2+1} =4A\)
Pour \(k=6, \; \; A^{2 \times 3}=4A^2\)
Sauf que là, tout devient désordonné. Exprimer chaque expression en fonction du rang de l’expression devient mission quasi impossible à cause de la décomposition des entiers entre la définition d’un terme pair ou impair.
Ici, l’astuce va en fait consister à séparer les puissances de rang pair des expressions de rang impair et de faire deux nouvelles itérations simultanément.
Pour les puissances de rang pair :
Pour \(k=0, \; \; A^{2 \times 0}=I\)
Pour \(k=2, \; \; A^{2 \times 1}=A^2\)
Pour \(k=4, \; \; A^{2 \times 2}=2A^2\)
Pour \(k=6, \; \; A^{2 \times 3}=4A^2\)
…
Pour les puissances de rang impair :
Pour \(k=1, \; \; A^{2 \times 0+1}=A\)
Pour \(k=3, \; \; A^{2 \times 1+1}=2A\)
Pour \(k=5, \; \; A^{2 \times 2+1} =4A\)
…
Sauf qu’en faisant cela, les rangs ne se suivent plus. Il y a un rang manquant entre chaque expression à chaque fois. On va donc devoir trouver une nouvelle suite de rangs. Pour cela, on recommence les compteurs.
Pour les expressions de rang pair :
Pour \(k={\color{red} 0}, \; \; A^{2 \times 0}=A^{0}=I\)
Pour \(k={\color{red}1}, \; \; A^{2 \times 1}=A^2\)
Pour \(k={\color{red}2}, \; \; A^{2 \times 2}=2A^2\)
Pour \(k={\color{red}3}, \; \; A^{2 \times 3}=4A^2\)
Et donc, on procède comme dans les exemples précédents : on exprime chaque expression en fonction du rang de l’expression.
Pour \(k={\color{red} 0}, \; \; A^{2 \times 0}=A^{\color{red} 0}=I\)
Pour \(k={\color{red}1}, \; \; A^{2 \times {\color{red}1}}=2^0A^2=2^{{\color{red}1}-1}A^2\)
Pour \(k={\color{red}2}, \; \; A^{2 \times {\color{red}2}}=2^1A^2=2^{{\color{red}2}-1}A^2\)
Pour \(k={\color{red}3}, \; \; A^{2 \times {\color{red}3}}=4A^2=2^2A^2=2^{{\color{red}3}-1}A^2\)
…
De même, pour les puissances de rang impair :
Pour \(k={\color{red}0}, \; \; A^{2 \times 0+1}=A\)
Pour \(k={\color{red}1}, \; \; A^{2 \times 1+1}=2A\)
Pour \(k={\color{red}2}, \; \; A^{2 \times 2+1} =4A\)
Et donc, on procède comme dans les exemples précédents : on exprime chaque expression en fonction du rang de l’expression.
Pour \(k={\color{red}0}, \; \; A^{2 \times {\color{red}0}+1}=2^{\color{red}0}A\)
Pour \(k={\color{red}1}, \; \; A^{2 \times {\color{red}1}+1}=2^{\color{red}1}A\)
Pour \(k={\color{red}2}, \; \; A^{2 \times {\color{red}2}+1} =2^{\color{red}2}A\)
…
Étape 3
On peut donc conjecturer nos deux relations.
Pour les puissances de rang pair :
Pour \(k={\color{red}1}, \; \; A^{2 \times {\color{red}1}}=2^{{\color{red}1}-1}A^2\)
Pour \(k={\color{red}2}, \; \; A^{2 \times {\color{red}2}}=2^{{\color{red}2}-1}A^2\)
Pour \(k={\color{red}3}, \; \; A^{2 \times {\color{red}3}}=2^{{\color{red}3}-1}A^2\)
…
\(\fbox{\(\text{Pour} \; k={\color{orange}n}, \; \; A^{2 \times {\color{orange}n}}=2^{{\color{orange}n}-1}A^2\)}\)
N.B. : Tu auras remarqué qu’on a enlevé l’expression du terme en \(k=0\), car elle ne rejoint pas le cas général (il ne faudra pas oublier de la rajouter à la fin, on la laisse de côté pour l’instant). Cette conjecture sera donc à montrer sur \(\mathbb N^*\) et non sur \(\mathbb N\)
Pour les puissances de rang impair :
Pour \(k={\color{red}0}, \; \; A^{2 \times {\color{red}0}+1}=2^{\color{red}0}A\)
Pour \(k={\color{red}1}, \; \; A^{2 \times {\color{red}1}+1}=2^{\color{red}1}A\)
Pour \(k={\color{red}2}, \; \; A^{2 \times {\color{red}2}+1} =2^{\color{red}2}A\)
…
\(\fbox{\(\text{Pour} \; k={\color{orange}n}, \; \; A^{2 \times {\color{orange}n}+1} =2^{\color{orange}n}A\)}\)
Ainsi, on commence la rédaction de sa copie par :
« Montrons par récurrence que \(
\begin{cases}
\forall n \in \mathbb N^*, A^{2n}=2^{n-1}A \\
\forall n \in \mathbb N, A^{2n+1}=2^{n}A^2
\end{cases}
\) »
Et on n’oublie pas de conclure en y ajoutant le terme en \(n=0\) qui, on le rappelle, ne rejoint pas le cas général.
Ainsi :
\[\fbox{\(
\begin{cases}
A^0=I \\
\forall n \in \mathbb N^*, A^{2n}=2^{n-1}A \\
\forall n \in \mathbb N, A^{2n+1}=2^{n}A^2
\end{cases}
\)}\]
Les écueils à éviter
L’écueil majeur lorsque l’on s’est trop habitué à faire un raisonnement par itération est que, parfois, la question nous demande directement de montrer une relation par récurrence, et on s’empresse de faire tout le raisonnement par itération sur son brouillon pour enfin conjecturer la relation qu’on veut montrer par récurrence. Sauf qu’en faisant cela, on a perdu énormément de temps car dans tous les cas, on devra montrer cette relation par récurrence.
N’hésite pas à consulter toutes nos ressources mathématiques !