Cet article te propose 10 astuces sur la notation Vect (sous-espace engendré), expliquées comme tu ne l’as jamais vu ! Il s’adresse aussi bien aux bizuths, aux carrés que aux cubes (car il est pour tous les niveaux !)
Compatible maths appliquées et maths approfondies.
Tu peux aussi consulter nos autres astuces
10 astuces sur min et max – Tous niveaux
8 astuces sur les sommes – Niveau intermédiaire
Soit \(n \in \mathbb N^*\)
Dans tout cet article, on considère \(E\) un \(\mathbb R\)-espace vectoriel, \((u_{i})_{1 \le i \le n}\) une famille de vecteurs de \(E\) et \(A\) et \(B\) deux parties de \(E\)
Rappels préliminaires sur le Vect
Définition du Vect (sous espace engendré)
C’est l’ensemble des combinaisons linéaires des vecteurs \((u_{i})_{1 \le i \le n}\) qui est un sous-espace vectoriel de \(E\). Il s’agit du sous-espace vectoriel engendré par les vecteurs \((u_{i})_{1 \le i \le n}\)
A savoir
Soit \(x \in E\)
Si on a \(\exists a_1 \in \mathbb R, x=a_1u_1\), on peut alors écrire que \(x \in \text{Vect}(u_1)\)
Si on a \(\exists (a_1,a_2) \in \mathbb R^2, x=a_1u_1+a_2u_2\), on peut alors écrire que \(x \in \text{Vect}(u_1,u_2)\)
…
Plus généralement, si on a \(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^na_iu_i\), on peut alors écrire que \(x \in \text{Vect}((u_{i})_{1 \le i \le n})\)
1) Le Vect peut s’écrire sous forme d’ensemble
Soit \(E\) un espace vectoriel et \(u \in E\)
\(\text{Vect}(u)=\{au, a \in \mathbb R \}\)
\(\text{Vect}(u,v)=\{au+bv, (a,b) \in \mathbb R^2 \}\)
…
\(\text{Vect}((u_{i})_{1 \le i \le n})=\left\{\displaystyle \sum_{k=1}^na_iu_i, (a_{i})_{1 \le i \le n} \in \mathbb R^n \right\}\)
2) Représentation graphique d’un Vect
Pour parfaitement comprendre qu’est-ce qu’un espace engendré, il est bon d’effectuer sa représentation graphique dans \(\mathbb R\) et dans \(\mathbb R^2\)
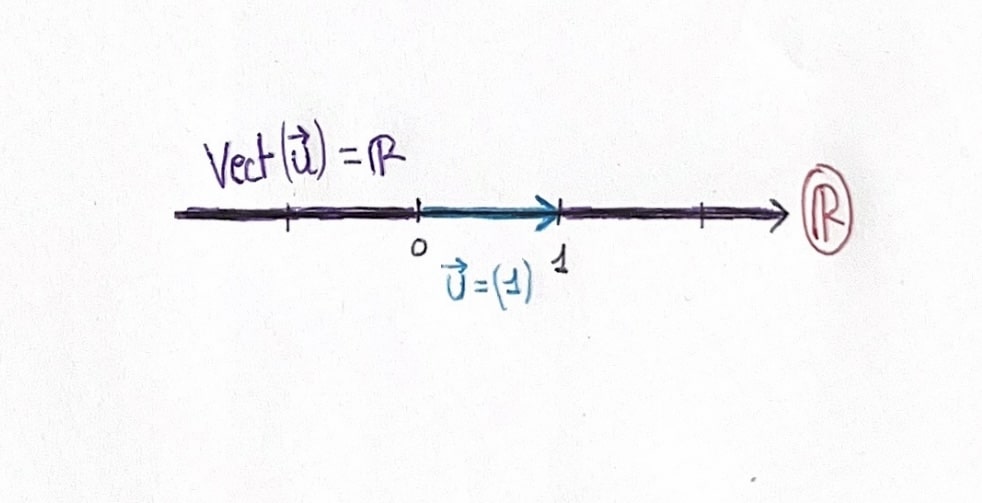
En fait, lorsque l’on a un vecteur \(\vec{u}\) (qui peut être vu comme un segment dans l’espace), ce vecteur peut engendrer une droite qui passera par ce vecteur : c’est comme cela qu’on obtient le \(\text{Vect}(\vec{u})\)
Ainsi, comme vu visuellement dans le graphique ci-dessus, on comprend pourquoi \(\text{Vect}(1)=\mathbb R\)
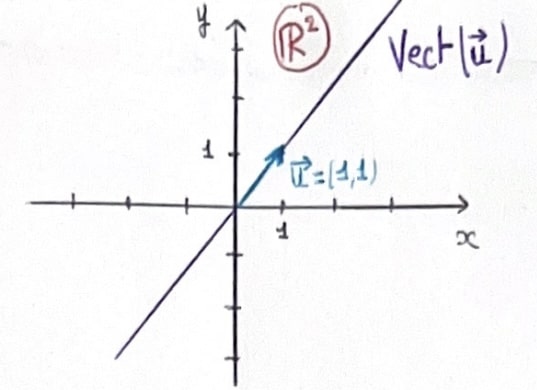
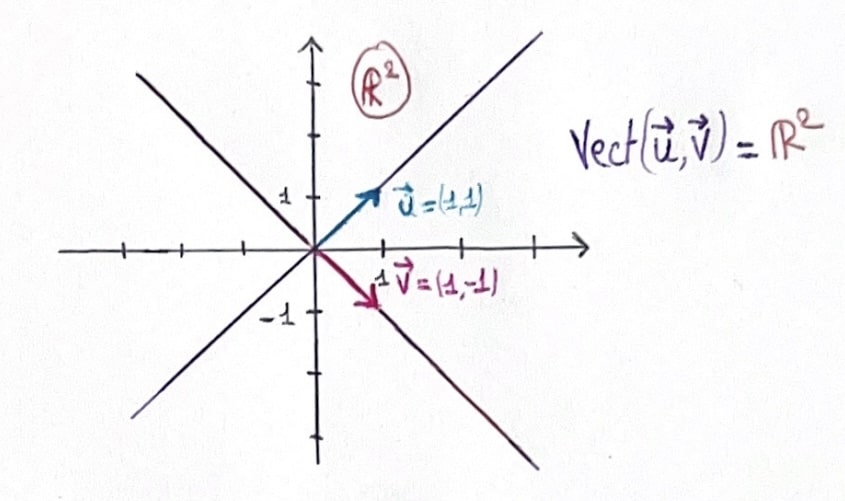
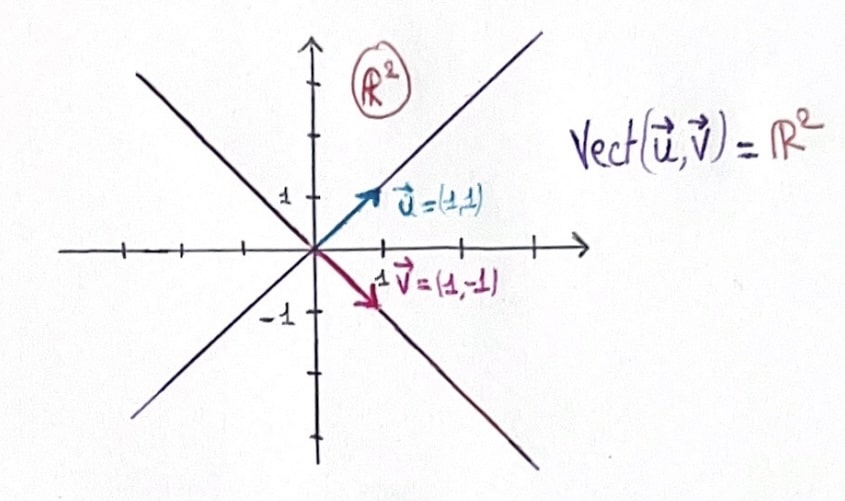
En fait, quand on a deux vecteurs non colinéaires \(\vec{u}\) et \(\vec{v}\), lorsque l’on considère leurs Vect, on obtient le plan de \(\mathbb R^2\). On peut donc écrire que \(\text{Vect}(\vec{u},\vec{v})=\mathbb R^2\)
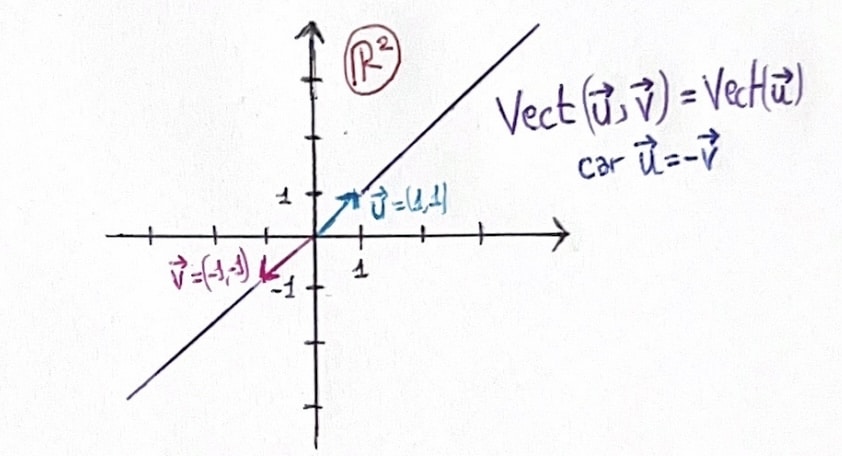
Voilà la représentation graphique de ce qu’il se passe lorsque deux vecteurs sont colinéaires (ici \(\vec{u}=-\vec{v}\), ce qui explique pourquoi on peut ôter un vecteur dans le vect (car visuellement ils se situent sur la même droite du \(\text{Vect}(\vec{u})\)
3) Simples propriétés sur le Vect
· \(\text{Vect}((u_{i})_{1 \le i \le n}) \subset E\) (car on rappelle avant tout que le vect est un sous-espace vectoriel de E, et ceci est bien une propriété fondamentale d’un sous-espace vectoriel)
· \(\text{Vect}(0)=0\)
· \(\text{Vect}(\emptyset)=\{0\}\) (par convention)
· Si \(A \subset B\) alors \(\text{Vect}(A) \subset \text{Vect}(B)\)
Donc on en déduit que \(\text{Vect}((u_1,u_2)) \subset \text{Vect}((u_1,u_2,u_3))\) car les vecteurs de la première famille sont contenus dans les vecteurs de la seconde famille.
· \(A \subset \text{Vect}(A)\)
Donc on peut en déduire que \(u \in \text{Vect}((u))\), mais aussi que \(u_1 \in \text{Vect}((u_1,u_2))\), etc.
· \(\text{Vect}((\text{Vect}(A))=\text{Vect}(A)\)
4) La propriété \(\forall \alpha \in \mathbb R^*, \text{Vect}(u)=\text{Vect}(\alpha u)\) est très utile !
Par exemple lorsque l’on a un vect avec des fractions, on peut les supprimer pour simplifier les calculs éventuels !
Exemple :
Pour \(u=\begin{pmatrix} \frac{1}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix}\) et \(\alpha=2\), on a :
\(\text{Vect}\left(\begin{pmatrix} \frac{1}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix}\right)=\text{Vect}\left(2.\begin{pmatrix} \frac{1}{2} \\ -\frac{1}{2} \\ 1 \end{pmatrix}\right)=\text{Vect}\left(\begin{pmatrix} \frac{2}{2} \\ -\frac{2}{2} \\ 2.1 \end{pmatrix}\right)=\text{Vect}\left(\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}\right)\)
Attention, cette propriété ne marche surtout pas pour un \(\alpha\) nul !
Lorsque \(\alpha=0\), on aura seulement \(\text{Vect}(\alpha u) \subset \text{Vect}(u)\)
5) Calculer la dimension d’un Vect
Il faut faire attention à ne pas dire n’importe quoi à propos de la dimension du vect. Par exemple : la dimension du vect n’est sûrement pas égale aux nombre de vecteurs que compose la famille engendrée, surtout pas !!
Ceci est vrai seulement lorsque la famille en question est libre.
Ainsi, si la famille \((u_{i})_{1 \le i \le n}\) est libre (et est constituée de \(n\) vecteurs), alors \(\text{dim}(\text{Vect}((u_{i})_{1 \le i \le n}))=n\)
Exemple :
Soit la famille \((u_1,u_2,u_3)\) de \(E\) telle qu’elle soit libre.
On a \(\text{dim}(\text{Vect}((u_1,u_2,u_3)))=3\), mais
\(\text{dim}(\text{Vect}((u_1,u_2,u_3,u_4))\ne 4\), en effet, d’après les astuces précédentes,
\(\text{Vect}((u_1,u_2,u_3,u_1))=\text{Vect}((u_1,u_2,u_3))\), donc
\(\text{dim}(\text{Vect}((u_1,u_2,u_3,u_4)))= 3\)
6) Si \(f\) est linéaire, alors \(f(\text{Vect}((u_{i})_{1 \le i \le n}))=\text{Vect}(f((u_{i}))_{1 \le i \le n})\)
Cette propriété n’est pas vraiment au programme officiel mais on pourra la considérer comme quasiment admise car elle découle de la définition d’une combinaison linéaire et de la linéarité de \(f\). En voici la démonstration (qui peut se faire par double inclusion).
Démonstration :
· Supposons que \(f\) est linéaire.
Soit \( y \in f(\text{Vect}((u_{i})_{1 \le i \le n}))\)
on peut écrire d’après la définition de l’image directe :
\( \exists x \in f(\text{Vect}((u_{i})_{1 \le i \le n})), y=f(x)\), or comme \(x \in f(\text{Vect}((u_{i})_{1 \le i \le n}))\), on a :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^na_iu_i\), d’où :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, y=\displaystyle f\left(\sum_{i=1}^na_iu_i\right)\), d’où par linéarité de \(f\) :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, y=\displaystyle \sum_{i=1}^na_if(u_i)\), ainsi, par définition d’un sous-espace engendré (ou par définition du Vect) :
\(y \in \text{Vect}(f((u_{i}))_{1 \le i \le n})\)
Ainsi, \(f(\text{Vect}((u_{i})_{1 \le i \le n})) \subset \text{Vect}(f((u_{i}))_{1 \le i \le n})\)
Soit alors \(y \in \text{Vect}(f((u_{i}))_{1 \le i \le n})\)
on a donc par définition d’un sous-espace engendré :
\(\exists (a’_{i})_{1 \le i \le n} \in \mathbb R^n, y=\displaystyle \sum_{i=1}^na’_if(u_i)\), d’où par linéarité de \(f\) :
\(\exists (a’_{i})_{1 \le i \le n} \in \mathbb R^n, y=\displaystyle f\left(\sum_{i=1}^na’_iu_i\right)\), d’où par linéarité de \(f\), et en posant \(\displaystyle x’=\sum_{i=1}^na’_iu_i\), on a :
\( \exists x’ \in \text{Vect}((u_{i})_{1 \le i \le n}), y=f(x’)\), ainsi par définition de l’image directe :
\( y \in f(\text{Vect}((u_{i})_{1 \le i \le n}))\)
Donc \(\text{Vect}(f((u_{i}))_{1 \le i \le n}) \subset f(\text{Vect}((u_{i})_{1 \le i \le n}))\)
Ainsi :
\[\fbox{\(\text{Si} \; f \; \text{est linéaire, alors} \; f(\text{Vect}((u_{i})_{1 \le i \le n}))=\text{Vect}(f((u_{i}))_{1 \le i \le n})\)}\]
7) Permutation de vecteurs de la famille \((u_{i})_{1 \le i \le n}\) au sein du vect
\(\text{Vect}((u_{i})_{1 \le i \le n})\) n’est pas modifié si on permute deux vecteurs de \((u_{i})_{1 \le i \le n})\)
Par exemple, on a : \(\text{Vect}((u_1,u_2,u_3)=\text{Vect}((u_3,u_2,u_1))\)
8) Cas où un \(u_i\) est combinaison linéaire des autres vecteurs de la famille \((u_{i})_{1 \le i \le n}\)
Si pour tout \(i \in [\![1,n]\!]\) on a \(u_i\) qui est combinaison linéaire des autres vecteurs, alors \(\text{Vect}((u_{j})_{1 \le j \le n}) = \text{Vect}(u_1,…,u_{i-1},u_{i+1},…,u_n)\), c’est-à-dire que l’on peut enlever \(u_i\) de la famille sans modifier le sous-espace engendré. En voici la démonstration (qui peut se faire par double inclusion).
Démonstration :
· Supposons que pour tout \(i \in [\![1,n]\!]\) on a \(u_i\) qui est combinaison linéaire des autres vecteurs
Soit \(x \in \text{Vect}((u_{i})_{1 \le i \le n})\)
Donc :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^na_iu_i\), d’où en distinguant le terme en \(i=j\) avec \(j \in [\![1,n]\!]\)
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, \forall j \in [\![1,n]\!], x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}a_iu_i+u_j\), or comme pour tout \(j \in [\![1,n]\!]\) on a \(u_j\) qui est combinaison linéaire des autres vecteurs, on peut écrire \(\forall j \in [\![1,n]\!], \in \exists (b_{i,j})_{1 \le i \le n} \in \mathbb R^n, u_j=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}b_{i,j}u_i\), donc :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, \forall j [\![1,n]\!], x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}a_iu_i+\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}b_{i,j}u_i\), d’où :
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, \forall j \in [\![1,n]\!], x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}(a_i+b_{i,j})u_i\), d’où en posant \(\forall j \in [\![1,n]\!], \forall i \in [\![1,n]\!], i\ne j \Rightarrow c_{i,j}=a_i+b_{i,j}\), on a :
\(\forall j \in [\![1,n]\!], \exists (c_{i,j})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}c_{i,j}u_i\)
Donc par définition d’un sous-espace engendré :
\(\forall j \in [\![1,n]\!], x \in \text{Vect}(u_1,…,u_{j-1},u_{j+1},…,u_n)\)
Soit alors pour tout \(j \in [\![1,n]\!]\), \(x \in \text{Vect}(u_1,…,u_{j-1},u_{j+1},…,u_n)\)
Donc par définition d’un sous-espace engendré, on a :
\(\forall j \in [\![1,n]\!], \exists (c_{i,j})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}c_{i,j}u_i\), d’où :
\(\forall j \in [\![1,n]\!], \exists (c_{i,j})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{\scriptstyle i=1\atop\scriptstyle i\ne j}^{n}c_{i,j}u_i+0 \times u_j\), d’où en posant \(\forall j \in [\![1,n]\!],c_{j,j}=0\), on a :
\(\forall j \in [\![1,n]\!], \exists (c_{i,j})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^{n}c_{i,j}u_i\),
ainsi par définition d’un sous-espace engendré :
\(x \in \text{Vect}((u_{i})_{1 \le i \le n})\)
On conclut alors par double inclusion que :
\[\fbox{\(\text{Si pour tout} \; i \in [\![1,n]\!] \; \text{on a} \; u_i \; \text{qui est combinaison linéaire des autres vecteurs, alors} \; \; \\ \text{Vect}((u_{i})_{1 \le i \le n}) = \text{Vect}(u_1,…,u_{i-1},u_{i+1},…,u_n)\)}\]
Exemples :
- Par exemple, comme 0 est combinaison linéaire de n’importe quel vecteur,
\(\text{Vect}(u_1,u_2,0,u_3)=\text{Vect}((u_1,u_2,u_3)\) - On comprend également que :
\(\text{Vect}(u,v,u+v)=\text{Vect}(u,v)\), puisque par définition, \(u+v\) est une combinaison linéaire de \(u\) et de \(v\). - Enfin, dernier exemple, pourquoi : \(\text{Vect}(2,1-X,4X+2)=\text{Vect}(1,X)\) ?
Tout simplement car les vecteurs \(2\), \(1-X\) et \(4X+2\), sont tous, chacun d’entre eux, des combinaisons linéaires des vecteurs \(1\) et \(X\)
En effet :
\(2=1.2+0.X\)
\(1-X=1.1+(-1).X\)
\(4X+2=2.1+4.X\)
9) La famille \((u_{i})_{1 \le i \le n})\) est génératrice de \(E\) si et seulement si \(\text{Vect}((u_{i})_{1 \le i \le n})=E\)
On utilise plus souvent cette propriété lorsque \((u_{i})_{1 \le i \le n}\) est une base de \(E\) (car qui dit base dit famille génératrice également). En voici la démonstration.
Démonstration :
· Supposons que la famille \((u_{i})_{1 \le i \le n})\) est génératrice de \(E\).
Soit \(x \in E\)
Par définition d’une famille génératrice :
\(\forall v \in E, \exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, v=\displaystyle \sum_{i=1}^na_iu_i\), d’où en pour \(v=x\)
\(\exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^na_iu_i\), et donc par définition d’un sous-espace engendré :
\(x \in \text{Vect}((u_{i})_{1 \le i \le n})\)
Donc \( E \subset \text{Vect}((u_{i})_{1 \le i \le n})\)
Et comme \(\text{Vect}((u_{i})_{1 \le i \le n})\) est un sous-espace vectoriel de (E\), alors
\(\text{Vect}((u_{i})_{1 \le i \le n}) \subset E\)
Ainsi, \(\text{Vect}((u_{i})_{1 \le i \le n})=E\)
· Supposons alors que \(\text{Vect}((u_{i})_{1 \le i \le n})=E\)
Donc on peut écrire que \( E \subset \text{Vect}((u_{i})_{1 \le i \le n})\), ce qui se traduit par :
\(\forall x \in E, x \in \text{Vect}((u_{i})_{1 \le i \le n})\), i.e.
\(\forall x \in E, \exists (a_{i})_{1 \le i \le n} \in \mathbb R^n, x=\displaystyle \sum_{i=1}^na_iu_i\)
Donc par définition d’une famille génératrice, on en conclut que \((u_{i})_{1 \le i \le n})\) forme une famille génératrice de \(E\).
Ainsi :
\(\fbox{\(\text{La famille} \; (u_{i})_{1 \le i \le n}) \; \text{est génératrice de E si et seulement si} \; \text{Vect}((u_{i})_{1 \le i \le n})=E\; \; \)}\)
10) On a l’égalité \(\text{Vect}(A \cup B)=\text{Vect}(A)+\text{Vect}(B)\)
Démonstration :
D’après l’astuce n°3, on a : si \( C \subset D\) alors \(\text{Vect}(C) \subset \text{Vect}(D)\), d’où, comme :
\( A \subset A \cup B\) et \( B \subset A \cup B\), alors :
\(\text{Vect}(A) \subset \text{Vect}(A \cup B)\) et \(\text{Vect}(B) \subset \text{Vect}(A \cup B)\)
On en déduit donc que :
\(\text{Vect}(A)+\text{Vect}(B) \subset \text{Vect}(A \cup B)\)
De plus, on a :
\(\text{Vect}(A) \subset \text{Vect}(A)+\text{Vect}(B)\) et
\(\text{Vect}(B) \subset \text{Vect}(A)+\text{Vect}(B)\)
Donc :
\(\text{Vect}(A) \cup \text{Vect}(B) \subset \text{Vect}(A)+\text{Vect}(B)\)
Ainsi :
\[\fbox{\(\text{Vect}(A \cup B)=\text{Vect}(A)+\text{Vect}(B)\)}\]
Tu veux apprendre comment appréhender et intérioriser tous ces astuces ? Alors consulte : Le carnet d’astuces en maths : une bonne idée ?
N’hésite pas à consulter toutes nos autres ressources mathématiques !