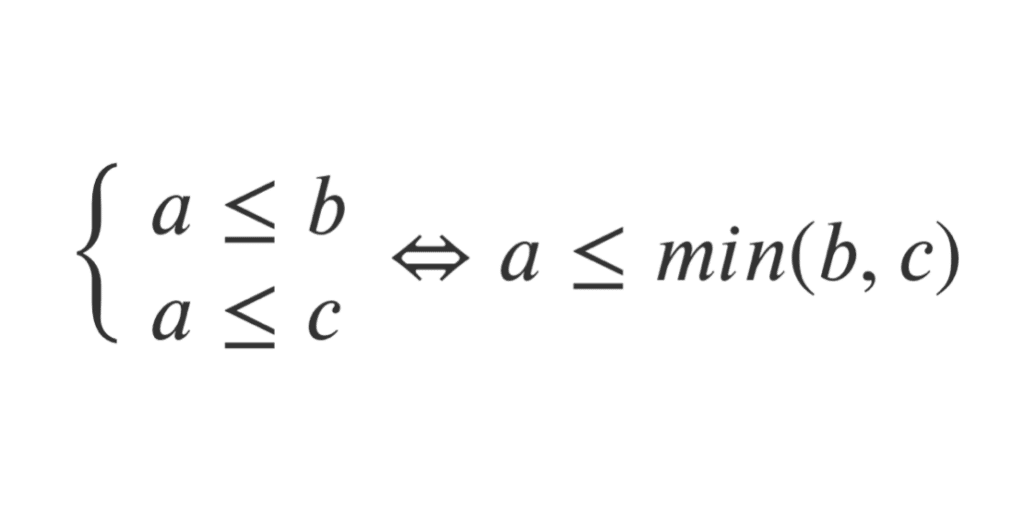Cet article te propose 10 astuces sur min et max. Il s’adresse aussi bien aux bizuths, aux carrés que aux cubes.
Compatible maths appliquées et maths approfondies.
Tu peux aussi consulter nos astuces sur les sommes :
8 astuces sur les sommes – Niveau intermédiaire
10 astuces sur les sommes – Niveau avancé
10 astuces sur les sommes – Niveau débutant
1) Transformer deux inégalités en un min ou un max
Soient \((a,b,c) \in \mathbb R^3\).
Cette propriété est tellement utile, mais tellement peu connue de tous les préparationnaires :
\(
\begin{cases}
a \le b \\
a \le c
\end{cases}
\Leftrightarrow a \le min(b,c)\)
De même :
\(
\begin{cases}
b \le a \\
c \le a
\end{cases}
\Leftrightarrow max(b,c) \le a\)
2) Généralisation de l’astuce précédente
Soit \(n \in \mathbb N^*\).
Soit \((x_i)_{1 \le i \le n} \in \mathbb R^n\), soit \(a \in \mathbb R\).
Si on fait de même, mais cette fois-ci pour trois inégalités, on a :
\(
\begin{cases}
a \le x_1 \\
a \le x_2 \\
a \le x_3
\end{cases}
\Leftrightarrow a \le min(x_1,x_2,x_3)\)
Et maintenant, pour 4 :
\(
\begin{cases}
a \le x_1 \\
a \le x_2 \\
a \le x_3 \\
a \le x_4
\end{cases}
\Leftrightarrow a \le min(x_1,x_2,x_3,x_4)\)
Et pour un \(x_i\) quelconque :
\(\displaystyle \forall i \in [\![1,n]\!], a \le x_i \Leftrightarrow a \le \min_{x \in [\![1,n]\!]}(x_i)\)
Et, encore plus généralement, pour un \(x\) quelconque, on aura donc :
\(\displaystyle \forall x \in E, a \le x \Leftrightarrow a \le \min_{x \in E}(x)\)
(Comme l’inégalité est vraie pour tout \(x \in E\), alors elle est vraie en particulier pour les valeurs de \(x\) lorsque \(x\) est minimal).
Attention, tous ces résultats marchent, car le minorant est toujours le même (ici \(a\)). Si le minorant est différent, c’est totalement mort, ça ne marchera plus !
Tous ces résultats sont bien évidemment analogues pour le \(\max\).
3) Définition du min et du max
Cette définition est très utile à savoir (même si elle n’est pas vraiment dans le cours, elle relève du bon sens, car les applications \(\min\) et \(\max\), elles, sont bien dans le cours).
\(
\forall (i,j) \in \mathbb N^2,\max(i,j)=
\begin{cases}
i &\text{si} \ j<i \\
j &\text{si} \ i<j
\end{cases}
\)
et
\(
\forall (i,j) \in \mathbb N^2,\min(i,j)=
\begin{cases}
i &\text{si} \ i<j \\
j &\text{si} \ j<i
\end{cases}
\)
4) Écriture alternative des ensembles qui utilisent min et max
Tu rencontres parfois ces notations : \(\displaystyle \max_{i \in I}(u_i)\) ou \(\displaystyle \max_{x \in E}(f(x))\).
En fait, ces notations cachent des ensembles cachés que tu peux écrire de cette façon :
\(\displaystyle \max_{i \in I}(u_i)=\max\{u_i, i \in I\}\)
\(\displaystyle \max_{x \in E}(f(x))=\max\{u_i, i \in I\}\)
Les notations sont bien évidemment analogues pour le \(\min\) (et les \(\sup\) et \(\inf\)).
5) Astuce courante pour majorer un max
Soit \(n \in \mathbb N^*\).
Qu’est-ce qui peut être plus grand qu’un max ? Cette astuce peut être bien utile…
On a \(\displaystyle \max_{1 \le i \le n}(|u_i|) \le \sum_{i=1}^n|u_i|\).
En effet, dans la somme, il y a forcément la valeur maximale \(\max_{1 \le i \le n}(|u_i|)\) à laquelle on ajoute d’autres valeurs qui sont positives, donc la somme sera forcément plus grande que le max.
Attention, cette astuce ne marche que pour des valeurs positives !
6) Déterminer la limite des \(x_i^{(p)} \in ]-1,1[\) grâce au max
Soit \(n \in \mathbb N^*\).
La propriété suivante est intéressante : \(\lim \limits_{p \to +\infty} \displaystyle \left(\max_{1 \le i \le n}(|x_i|^{(p)}\right)=0 \Rightarrow \forall i \in [\![1,n]\!], \lim \limits_{p \to +\infty}(|x_i|^{(p)})=0\).
Démonstration :
· Supposons que \(\lim \limits_{p \to +\infty}\left(\max_{1 \le i \le n}(|x_i|^{(p)}\right)=0 \)
On peut écrire par définition du \(\max\) que :
\(\forall p \in \mathbb N, \forall i \in [\![1,n]\!], 0 \le |x_i|^{(p)} \le \displaystyle \left(\max_{1 \le i \le n}(|x_i|^{(p)}\right)\)
D’où, comme \(\lim \limits_{p \to +\infty} \displaystyle \left(\max_{1 \le i \le n}(|x_i|^{(p)}\right)=0 \), d’après le théorème de l’encadrement (\(p \leftarrow \infty\))
\(\lim \limits_{p \to +\infty} (|x_i|^{(p)})=0 \), c’est-à-dire
\(\lim \limits_{p \to +\infty} (x_i^{(p)})=0\)
Ainsi, on a bien : \(\lim \limits_{p \to +\infty} \displaystyle \left(\max_{1 \le i \le n}(|x_i|^{(p)}\right)=0 \Rightarrow \forall i \in [\![1,n]\!], \lim \limits_{p \to +\infty}(|x_i|^{(p)})=0\)
7) Passage du min au max
Cette astuce assez logique est parfois utile.
\(\displaystyle \forall (a,b) \in \mathbb R^2, \max(-a,-b)=-\min(a,b)\).
Cela se démontre grâce aux formules sur le max et le min.
D’où, en généralisant :
\(\displaystyle \forall (x_i)_{1 \le i \le n} \in \mathbb R^n, \max_{1 \le k \le n}(-x_k)=-\min_{1 \le k \le n}(x_k)\)
8) Opérations sur les min et max
Soit \((a,b) \in \mathbb R^2\).
Astuces toujours assez utiles qu’il est bien de savoir :
\(\max(a,b)+\min(a,b)=a+b\)
En effet :
Si \(\min(a, b)=a\) et \(\max(a,b)=b\), alors \(\min(a,b)+\max(a,b)=a+b\)
Si \(\min(a, b)=b\) et \(\max(a,b)=a\), alors \(\min(a,b)+\max(a,b)=b+a\)
De même :
\(\max(a,b)-\min(a,b)=|a-b|\)
En effet :
Si \(\min(a, b)=a\) et \(\max(a,b)=b\), alors \(\max(a,b)-\min(a,b)=b-a=-(a-b)\)
Si \(\min(a, b)=b\) et \(\max(a,b)=a\), alors \(\max(a,b)-\min(a,b)=a-b\)
Donc, dans tous les cas : \(\max(a,b)-\min(a,b)=|a-b|\)
Illustration graphique :
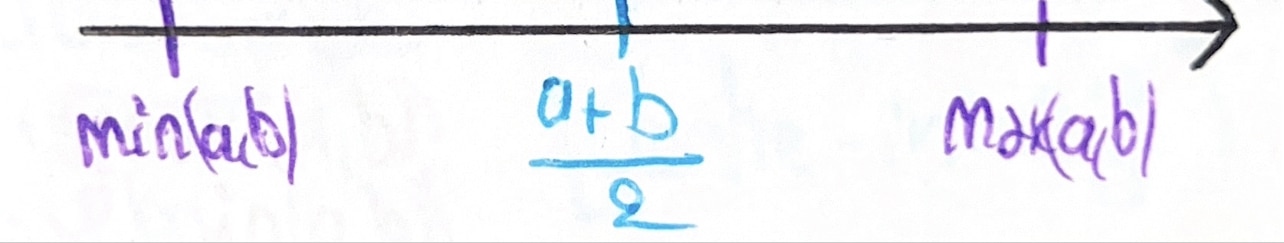
En effectuant l’addition et la soustraction membre à membre de ces deux résultats, on obtient :
\(
\forall (a,b) \in \mathbb R^2,
\begin{cases}
\max(a,b)=\frac{a+b+|a-b|}{2} \\
\min(a,b)=\frac{a+b-|a-b|}{2} \\
\end{cases}
\)
9) Composition du max et du min avec des fonctions croissantes et décroissantes
Attention, cette astuce est à la limite du programme. À utiliser avec précaution.
Soient \((a,b) \in \mathbb R^2\), \(n \in \mathbb N^*\) et \(\Phi\) une fonction bijective définie sur \(\mathbb R\).
Si \(\Phi\) est croissante :
\(\min(\Phi(a),\Phi(b))=\Phi(\min(a,b))\)
\(\max(\Phi(a),\Phi(b))=\Phi(\max(a,b))\)
Si \(\Phi\) est décroissante :
\(\min(\Phi(a),\Phi(b))=\Phi(\max(a,b))\)
\(\max(\Phi(a),\Phi(b))=\Phi(\min(a,b))\)
Donc, concrètement, comme \(i \mapsto \frac{1}{t}\) est décroissante et bijective sur \(\mathbb R_+^*\) :
\(\displaystyle \max_{1 \le i \le n}(\frac{1}{|x_i|})=\frac{1}{\min_{1 \le i \le n}(|x_i|)}\)
et comme \(\exp\) est croissante sur \(\mathbb R\) :
\(\displaystyle \max_{1 \le i \le n}(e^{x_i})=e^{\displaystyle \max_{1 \le i \le n}(x_i)}\)
N.-B. : Erreur fatale, les min et max ne sont pas linéaires !
Cependant, grâce à cette propriété, on peut en déduire la chose suivante :
Soient \(\alpha \in \mathbb R^+\) et \(f\) une fonction réelle.
Comme la fonction \(t \mapsto \alpha t\) est croissante sur \(\mathbb R\), on peut écrire :
\(\min(\alpha f))=\alpha\min(f)\)
\(\max(\alpha f))=\alpha\max(f)\)
Soient \(\alpha \in \mathbb R^-\) et \(f\) une fonction réelle.
Comme la fonction \(t \mapsto \alpha t\) est décroissante sur \(\mathbb R\), on peut écrire :
\(\min(\alpha f))=\alpha\max(f)\)
\(\max(\alpha f))=\alpha\min(f)\)
10) Croissance du max, décroissance du min
Soient \((a,b,c) \in \mathbb R^3\), \(E\) et \(F\) deux ensembles et \(f\) une fonction réelle.
Astuce très utile !
Si \(\{a,b\} \subset \{a,b,c\}\), alors \(
\begin{cases}
\max(a,b) \le \max(a,b,c) \\
\min(a,b,c) \le \min(a,b)
\end{cases}
\)
Donc, on en déduit sa généralisation :
Si \(E \subset F\), alors \(
\begin{cases}
\displaystyle
\sup_E(f) \le \sup_F(f) \\
\displaystyle \inf_F(f) \le \inf_E(f)
\end{cases}
\)
Explications :
· comme \(E \subset F\), il y a plus de valeurs pour trouver une valeur supérieure, d’où la croissance de l’opérateur ;
· comme \(E \subset F\), au contraire, il y a plus de valeurs pour trouver la valeur inférieure, d’où la décroissance de l’opérateur.
N.-B. : Différence entre max et sup (elle est minime).
La différence que tu dois retenir est que le sup n’est pas forcément atteint alors que le max l’est.
Donc, concrètement : \(\forall x \in E, \sup(f,g)=\max(f(x),g(x))\)
Tu veux apprendre comment appréhender et intérioriser tous ces astuces ? Alors consulte : Le carnet d’astuces en maths : une bonne idée ?
N’hésite pas à consulter toutes nos autres ressources mathématiques !