L’épreuve de mathématiques approfondies d’Ecricome est une épreuve importante car c’est la seule épreuve de mathématiques pour toutes les écoles Ecricome. En effet, elle est utilisée par de nombreuses écoles et tu peux la maitriser avec du dévouement et de la persévérance. Dans cet article, nous analyserons ma copie de Maths Ecricome 2023 notée 19,6/20 en découvrant toutes les méthodes et les astuces qui ont conduit à ce résultat. Mon objectif est ainsi de te montrer ce qui m’a permis d’avoir une telle note, en soulignant question par question tous les points positifs et négatifs de ma copie.
Exercice 1 : Les matrices commutantes
Partie I
Les sujets Ecricome commencent avec des questions classiques et il est donc important d’y répondre correctement et d’opter pour une rédaction soignée. Ainsi la première question de ce sujet nous fait simplement calculer deux produits de matrices puis déterminer les valeurs propres de ces produits qui sont sur les diagonales car les matrices sont triangulaires ! J’ai également introduit deux vecteurs appartenant aux sous espaces propres des matrices étudiées pour déterminer ces espaces.
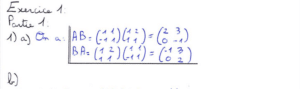

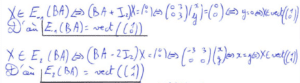
La question 2) est davantage technique car elle nécessite d’utiliser un raisonnement par l’absurde et de correctement le rédiger. J’ai donc considéré la négation de l’assertion demandée pour aboutir à un résultat incohérent. Ce résultat incohérent est simplement l’assertion que nous venons de refuser. Quant à la 2) b), j’ai utilisé le résultat que nous venions de démontrer pour aboutir au résultat attendu. D’où l’importance de prendre le temps nécessaire pour comprendre les résultats des questions précédentes !
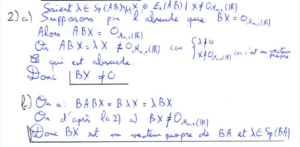
La question 3) demande elle aussi de réaliser un raisonnement par l’absurde, je l’ai donc rédiger de la même manière que dans la question précédente pour montrer une forme de cohérence dans ma copie. Finalement, pour obtenir le résultat de la 3) b) j’ai fait un troisième raisonnement par l’absurde et j’ai raisonner avec la dimension des images des matrices étudiées.
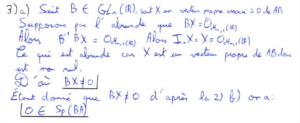

Dans la question 4), j’ai utilisé une stratégie pour gagner beaucoup de temps. On nous demande de montrer un résultat pour \(AB\) et \(BA\) en utilisant les résultats des questions 2) et 3). Or ces résultats ne concernent que \(AB\) et non \(BA\), j’ai donc écris qu’avec un raisonnement analogue on aurait trouvé les mêmes résultats que pour \(AB,\) ce qui m’a évité de tout refaire !
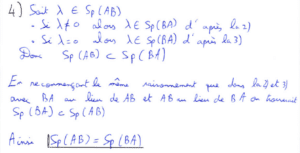
Finalement, la dernière question de cette première partie est probablement la plus dure car il fallait sortir du cas général pour trouver un contre exemple à l’assertion présentée. J’ai ainsi remarqué que la première question du sujet était bien un contre exemple qui convenait.
Partie II
Dans cette deuxième partie nous travaillons avec \(A,\) une matrice de taille \(n \times n,\) qui admet \(n\) valeurs propres distinctes. La première question de cette partie découle tout simplement du résultat : \(Q(A)=0\), nous avons bien un tel polynôme annulateur ! Ensuite, la 6) b) se fait encore avec un raisonnement par l’absurde ! Étant donné que c’est déjà le quatrième du sujet on peut gagner un peu de temps sur la rédaction. Ces deux résultats nous permettent bien de conclure que la famille étudiée est libre !

La question 7) est complexe car elle nécessite de démontrer plusieurs résultats. Dans un premier temps j’ai montré encore une fois par l’absurde que l’espace propre associé à \(\lambda\) est de dimension inférieur ou égal à 1 puis que \(X\) est un vecteur propre de \(A\) associé à \(\lambda.\) Ensuite, en remarquant que \( BAX = \lambda BX = ABX\) j’ai pu à la fois démontrer le résultat de la 7) b) et 7) c) en distinguant le cas où \(\lambda\) est nul et non nul. Finalement, la question 8) est la synthèse de la 7) a) et de la 7) b), c’est en rappelant ces deux résultats que nous arrivons au fait que tout vecteur propre de \(A\) est vecteur propre de \(B.\)
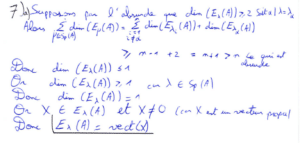

La question 9) vient utiliser le fait que la matrice \(A\) est diagonalisable ce qui se montre en utilisant le fait que \(A\) est une matrice de taille \(n \times n,\) qui admet \(n\) valeurs propres distinctes. Ce caractère diagonalisable nous permet de justifier l’existence de la base demandée puis avec la dimension des espaces propres nous pouvons construire une telle base. Je n’ai réalisé la question 9) b) qu’à moitié et j’ai pris le temps d’indiquer le résultat qui me manquait, cela me permet d’assurer une partie des points alloués à la question.


La question 10) a) est assez classique, il faut montrer qu’une application est bien linéaire puis montrer que c’est un isomorphisme. Cela se montre en se servant de la dimension de l’espace des antécédents de la fonction et de son image et du fait qu’un polynôme de degré inférieur ou égal à \(n\) qui a \(n+1\) racines réelles distinctes est le polynôme nul. En se servant du fait que l’application est donc bijective nous obtenons l’existence est l’unicité demandée dans la 10) b). Finalement, la 10) c) nécessite d’appliquer ce résultat de cours : si \(X_i\) est un vecteur propre de \(A\) associé à la valeur propre \(\lambda_i\) alors \(P(A)X_i=P(\lambda_i)X_i.\)
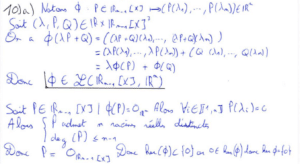

La dernière question de ce premier exercice commence par nous faire montrer qu’un ensemble est un espace vectoriel, il faut utiliser précisément la définition d’un espace vectoriel ! Ensuite, nous pouvons montrer l’égalité d’ensemble en procédant par double inclusion. Il fallait conclure en établissant un lien avec la question 6) a) qui nous affirme la liberté de la famille étudiée. Ainsi, nous avons bien que la dimension de l’espace vectoriel qui contient les matrices qui commutent avec \(A\) est \(n.\)
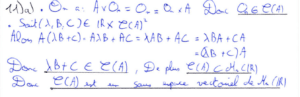

Exercice 2 : L’algèbre bilinéaire et les fonctions à plusieurs variables
Ce second exercice aborde plusieurs thèmes du programme, les fonctions à plusieurs variables, l’algèbre linéaire et bilinéaire. Il fallait dans un premier temps montrer qu’une application est un automorphisme, j’ai donc opté pour une décomposition sur une base de vecteurs propres d’un élément du noyau de \(f\) pour montrer le caractère injectif puis bijectif.

La deuxième exercice tisse un lien avec l’algèbre bilinéaire. La première question est une simple question de cours où il fallait donner la définition d’un endomorphisme symétrique ! Étant donné que \(f\) est symétrique on a donc que \({}^TA=A.\) De part la symétrie de \(A\) nous pouvons en déduire son caractère diagonalisable qui nous permet de répondre à la 2) c). Pour montrer, la double inégalité de la 2) d), j’ai fait le choix de raisonner en deux temps en décomposant le produit scalaire de \(f(x)\) par \(x.\) Finalement, pour répondre à la 2) e) j’ai utilisé l’inégalité que nous venons de démontrer.


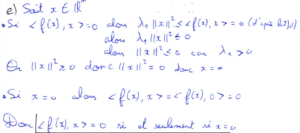
La question 3) nécessite beaucoup de calculs lourds avec des sommes de sommes et des multiplications de matrices. Cela nous permet d’exprimer différemment \(g(x)\) et sa dérivée partielle à l’ordre 1 tout en justifiant son caractère \(C^1\) du fait que \(g\) est polynomiale. En généralisant le calcul que nous venons de faire nous pouvons trouver toutes les dérivées partielles de \(g\) et en déduire l’égalité demandée.
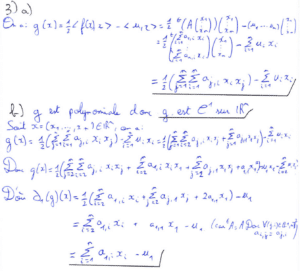
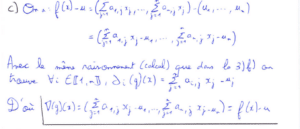
Pour montrer la question 4), j’ai raisonné à l’aide d’équivalences tout en utilisant la fonction réciproque de \(f\) qui existe bien d’après la 1).
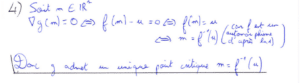
La question 5) nécessite de faire des longs calculs de produits scalaires, il est ici important de prendre son temps pour développer correctement les produits scalaires sans faire d’erreurs d’étourderie.
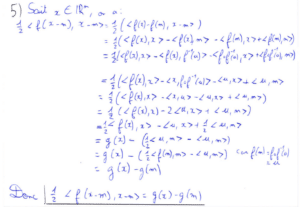
J’ai ensuite pu utiliser l’inégalité de la question 2) d) pour affirmer que \(g\) atteint un minimum global en \(m.\) Cela permet d’apporter une réponse à la question 6).
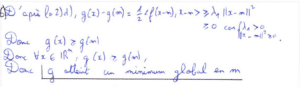
Exactement pareil que dans la question 5), il faut procéder à de longs calculs délicats pour aboutir aux résultats de la 7) a) et de la 7) b). Ces calculs consistent à développer les produits scalaires à gauche des égalités pour obtenir les membres de droites. J’ai ensuite fait le choix de passer la question 8) – tout en indiquant que j’admettais les résultats demandés – pour me concentrer davantage sur les questions suivantes.
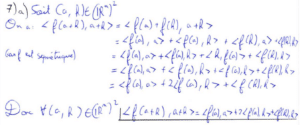
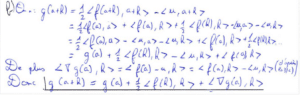
Pour montrer la convergence de la 9) a), j’ai utilisé le résultat de la 8) b) pour montrer la décroissance de la suite puis la question 6) pour montrer que cette suite est minorée, d’où sa convergence. Finalement, la question 9) c) peut se faire à l’aide de la question 9) b) et de l’indication du sujet pour montrer que la norme étudiée converge vers 0.

La question 10) était une question facile, il suffisait d’écrire la matrice associée à l’endomorphisme \(f\) et constater que cette matrice est symétrique ce qui justifie que \(f\) est un endomorphisme symétrique.

J’ai ensuite décidé d’arrêter le deuxième exercice pour passer au problème. En effet, le sujet était très long et il y a toujours beaucoup de points à gagner dans le problème en comparaison à ce deuxième exercice plus difficile.
Le problème : La fonction Zeta et les probabilités
Partie I
La première partie de ce problème nous fait étudier une fonction. La question 1) est la première question Python du sujet, elle nous fait programmer une fonction à l’aide de la bibliothèque Numpy.
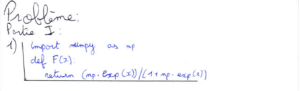
La seconde question consiste à démontrer le caractère \(C^{\infty}\) de \(f=F^{\prime}\) grâce au caractère \(C^{\infty}\) de la fonction exponentielle. Puis il fallait dériver deux fois la fonction \(F.\)

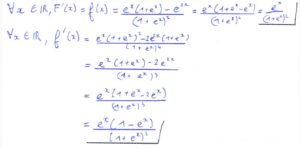
La question 3) était aussi abordable car il suffisait de réaliser l’étude des fonctions \(f\) et \(F\) et de dresser leur tableau de variations. Il fallait ensuite étudier la parité de \(f.\)

En utilisant le tableau de variation de la question 3), nous pouvions démontrer le caractère bijectif de \(F\) du fait de sa stricte croissance et de sa continuité. Il était ensuite possible de déterminer sa fonction réciproque en isolant \(x\) dans l’équation \(F(x)=y.\)

Partie II
La question 7) ne doit pas se faire directement. En effet, il faut d’abord démontrer que la série converge absolument d’après le critère de Riemann pour affirmer qu’elle converge.
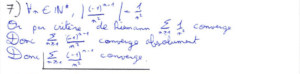
La question 8) pouvait se faire simplement en vérifiant que \(f\) est une densité de probabilité à l’aide de la définition d’une telle fonction.

Pour la question 9) il faut montrer que \(X\) admet une espérance et une variance. J’ai décidé de montrer leur existence en étudiant la convergence d’intégrales. J’ai donc montré que \(X\) admettait un moment d’ordre 2 à l’aide de la parité de \(f\), cela montre aussi qu’elle admet un moment d’ordre 1. Quant au résultat de la question 10), j’ai pu le montrer à l’aide du changement de variable \(x=-u.\)
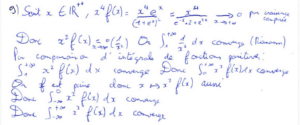

Finalement, avec du recul je pense avoir passé trop de temps sur les deux premiers exercices et pas assez sur le problème qui peut rapporter beaucoup de points facilement ! Il est ainsi recommandé de ne pas négliger le problème et de faire toutes les questions faciles qu’il contient et qui peuvent être nombreuses !
Conclusion
Cet article a pour objectif de partager mes expériences et conseils sur l’épreuve de mathématiques approfondies d’Ecricome, où j’ai obtenu la note de 19,6/20. En décrivant les forces et les faiblesses de ma copie avec des commentaires détaillés, mon but est de mettre en avant les stratégies, techniques de rédaction, et la préparation sérieuse qui m’ont aidé à réussir cette épreuve, et qui pourraient être bénéfiques pour toi aussi.
Les problèmes traités, qu’ils concernent l’algèbre linéaire, les probabilités ou les fonctions à plusieurs variables, soulignent l’importance de bien comprendre les concepts au programme, de rédiger avec clarté et d’utiliser des méthodes de résolution appropriées. Les questions de Python renforcent également le rôle crucial de la programmation dans les examens de concours.
J’espère que partager ma copie et mes méthodes pourra t’offrir une aide utile dans ta préparation aux épreuves de concours !
N’hésite pas à consulter toutes nos autres ressources mathématiques !