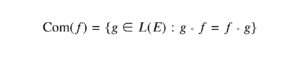L’épreuve de mathématiques approfondies d’EDHEC est une épreuve importante où de très bonnes notes sont accessibles. En effet, elle est utilisée par plusieurs écoles et tu peux la maîtriser avec du dévouement et de la persévérance. Dans cet article, nous analyserons ma copie de Maths EDHEC de 2023 notée 20/20, en découvrant toutes les méthodes et les astuces qui ont conduit à ce résultat. Mon objectif est ainsi de te montrer ce qui m’a permis d’avoir une telle note, en soulignant question par question tous les points positifs et négatifs de ma copie.
Le premier exercice : soigner sa rédaction
Partie I
Dans les sujets EDHEC et EML, la rédaction occupe une place très importante. C’est un critère de notation discriminant qui peut jouer en ta faveur lors des écrits.
Le premier exercice de ce sujet nous fait aborder des notions d’algèbre linéaire avec des questions sur des endomorphismes, des vecteurs et des valeurs propres. La première question de ce sujet est simple, car il nous suffit d’appliquer le théorème du rang. Cependant, il faut soigner sa rédaction dès les premières lignes.

La question 2) a) est déjà davantage technique, car il faut introduire des objets mathématiques : les colonnes de la matrice \(M\). Il faudra ensuite conclure en réalisant le calcul d’un produit matriciel.
Pour la 2) b), il faut d’un côté calculer la trace de \(M\) en se servant de sa définition et d’un autre côté calculer le produit \(LC.\) Finalement, la question 2) c) nécessite d’appliquer la question 2) a) et la 2) b) lorsque nous calculons \(M^2.\)
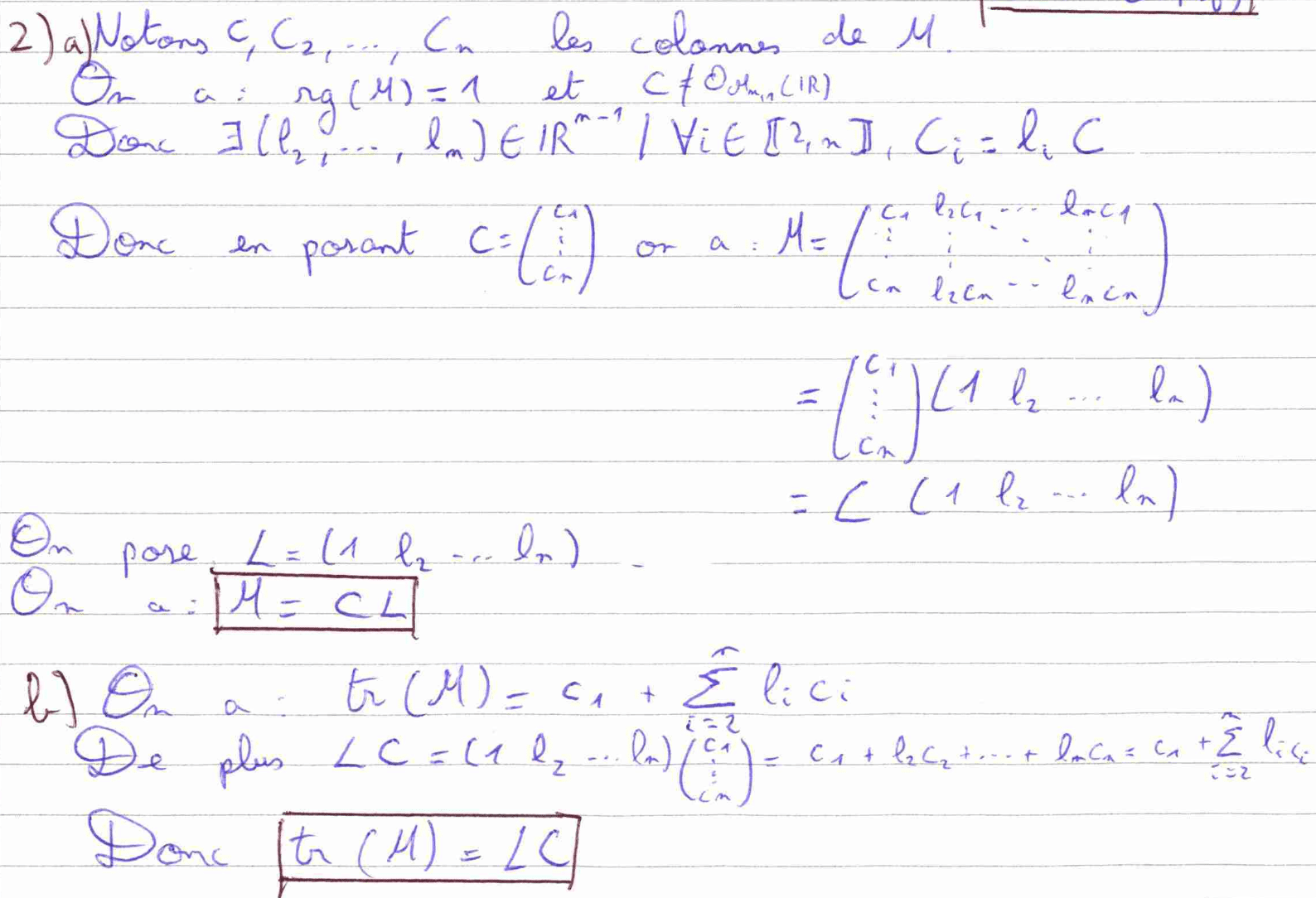

La question 3) nous fait utiliser le résultat de la 2) c). Cependant, il ne faut pas oublier de montrer que le vecteur \(C\) n’est pas une matrice colonne nulle : un oubli fréquent.

La question 4) nous fait appliquer les résultats des questions 1), 2) et 3). Cela montre bien toute l’importance de comprendre et d’admettre le résultat de chacune des questions, et ce, même si tu n’as pas réussi à les faire. Le raisonnement nécessite une réflexion sur les dimensions des espaces propres associés aux valeurs propres de \(f.\)
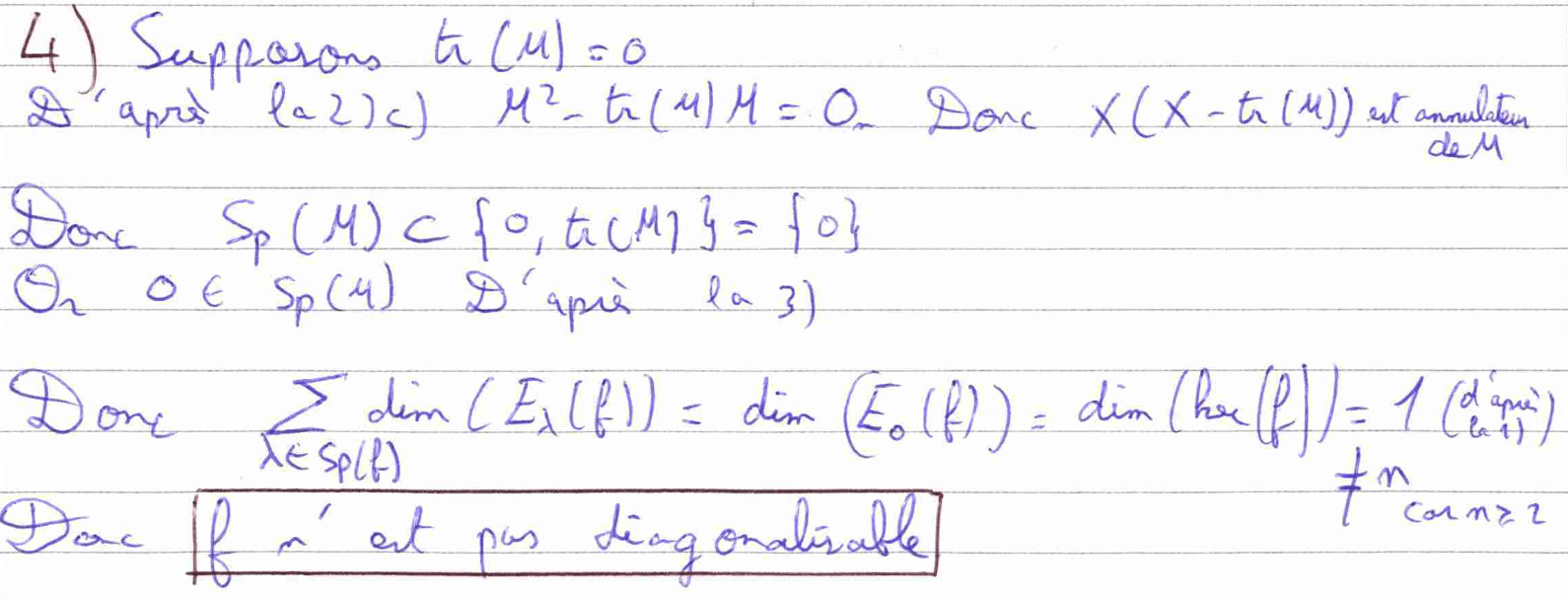
La dernière question de la partie I nous fait montrer que si la trace de \(M\) n’est pas nulle, alors \(f\) est diagonalisable. Il faut une fois de plus étudier les dimensions des espaces propres associés aux valeurs propres de \(f.\) Cela permet de montrer que la somme de ces dimensions vaut \(n.\)


Partie II
La première question de cette deuxième partie nous fait utiliser un raisonnement par l’absurde qui nécessite de longs calculs. Face à ce genre de questions, il faut être concentré et particulièrement vigilant. Cela te permettra d’éviter les erreurs d’étourderies et d’aboutir au résultat attendu.
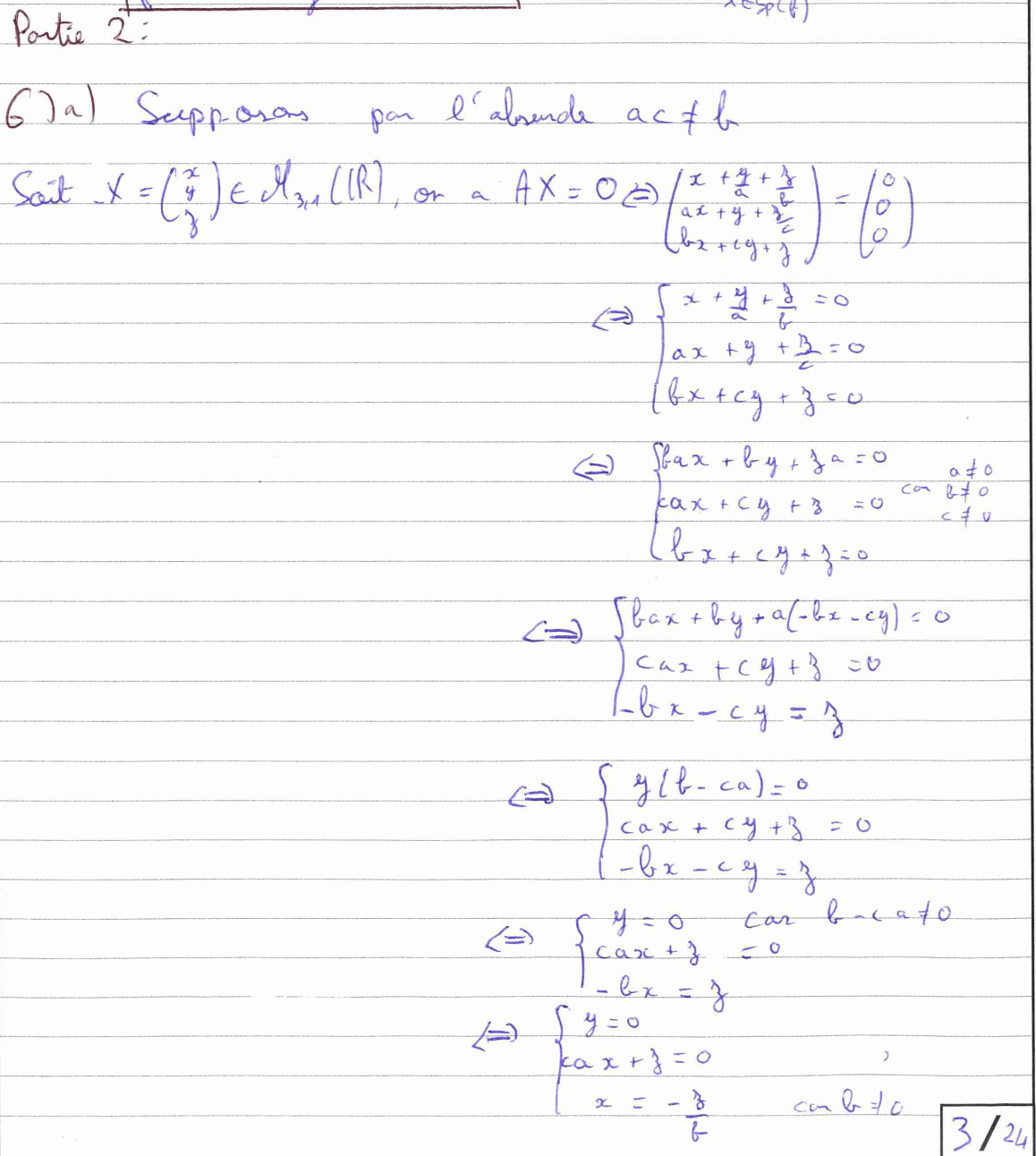
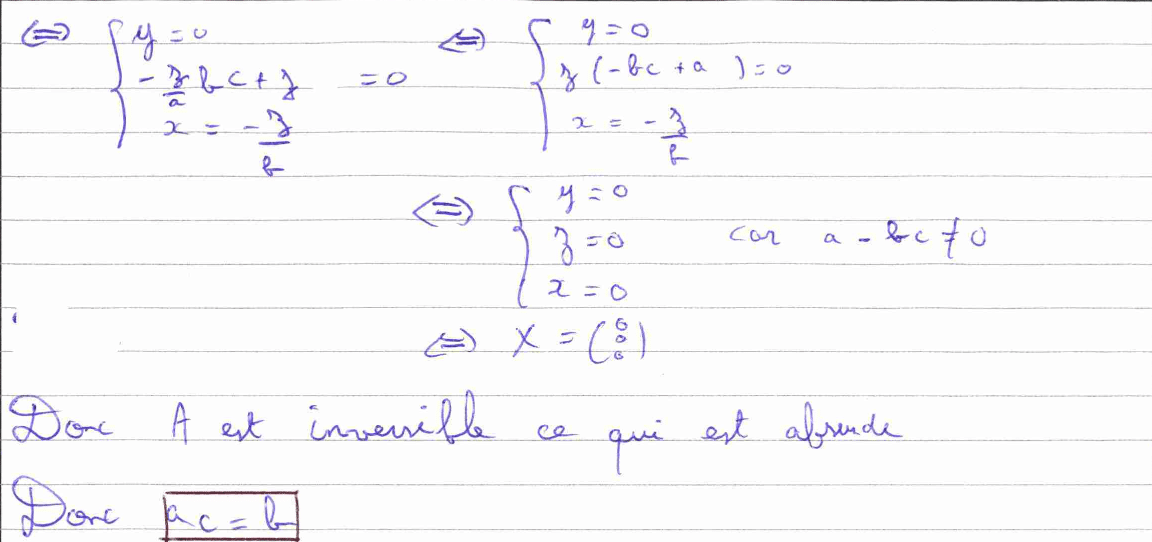
La question 6) b) est davantage technique, car elle nous fait utiliser la définition du rang avec un raisonnement par l’absurde pour montrer que deux vecteurs ne sont pas colinéaires. Un raisonnement peu courant mais qui peut être intéressant à mémoriser.
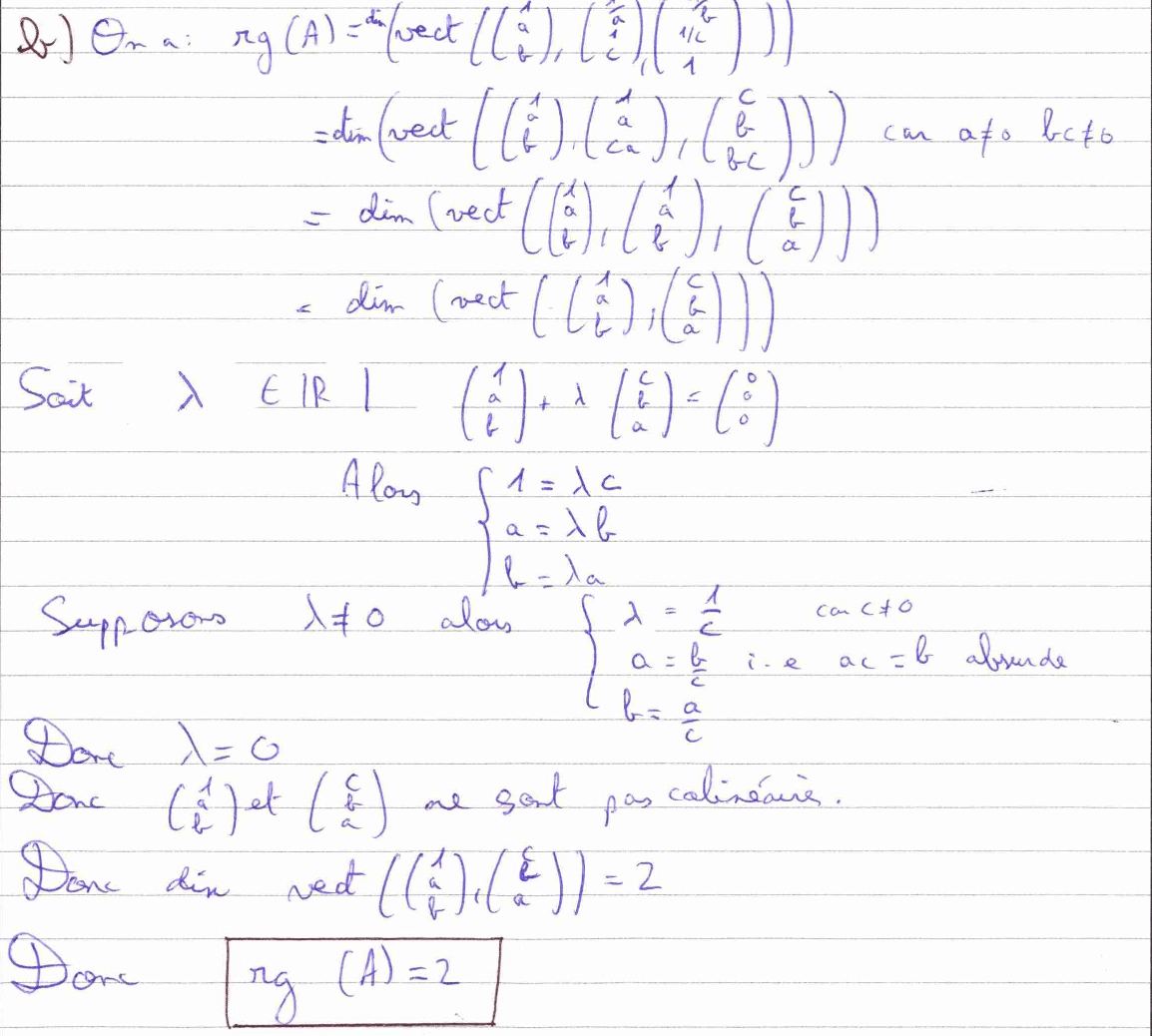
La question 7) a) te fait trouver les valeurs propres de \(g\) et te permet de conclure que cet endomorphisme est diagonalisable en raisonnant sur la dimension des espaces propres associés aux valeurs propres de \(g.\) Quant à la dernière question de ce premier exercice, elle nous fait démontrer que la matrice \(A\) et la matrice \(A^n\) sont colinéaires. Pour cela, il faut utiliser le caractère diagonalisable de \(A\) pour arriver à une expression de \(A^n\). En faisant sortir \(3^{n-1}\) en facteur, nous arrivons à montrer que \(A\) et \(A^n\) sont colinéaires.

Un deuxième exercice sur la loi de Pareto
Partie I
Commençons par rappeler que contrairement aux sujets HEC, il est courant que les parties des sujets EDHEC soient complètement indépendantes les unes des autres. C’est le cas ici avec un deuxième exercice qui porte sur les probabilités après un premier exercice d’algèbre linéaire.
Ce deuxième exercice porte sur les probabilités et plus précisément sur la loi de Pareto. Un thème déjà tombé dans le sujet Maths II 1995 qui est un classique pour s’entraîner sur les probabilités.
La question 1) nous fait montrer qu’une fonction est une densité. Cette question ne pose pas de problèmes particuliers, il faut cependant être vigilant à notre rédaction.

La question 2) est une question d’analyse, elle nous fait calculer plusieurs intégrales impropres. En termes de rédaction, il faut préciser que nous travaillons « sous réserve de convergence ». La convergence sera démontrée lorsque nous arriverons à trouver la valeur des intégrales qui sont des réels. De même, la question 3) consiste également à calculer une intégrale impropre.
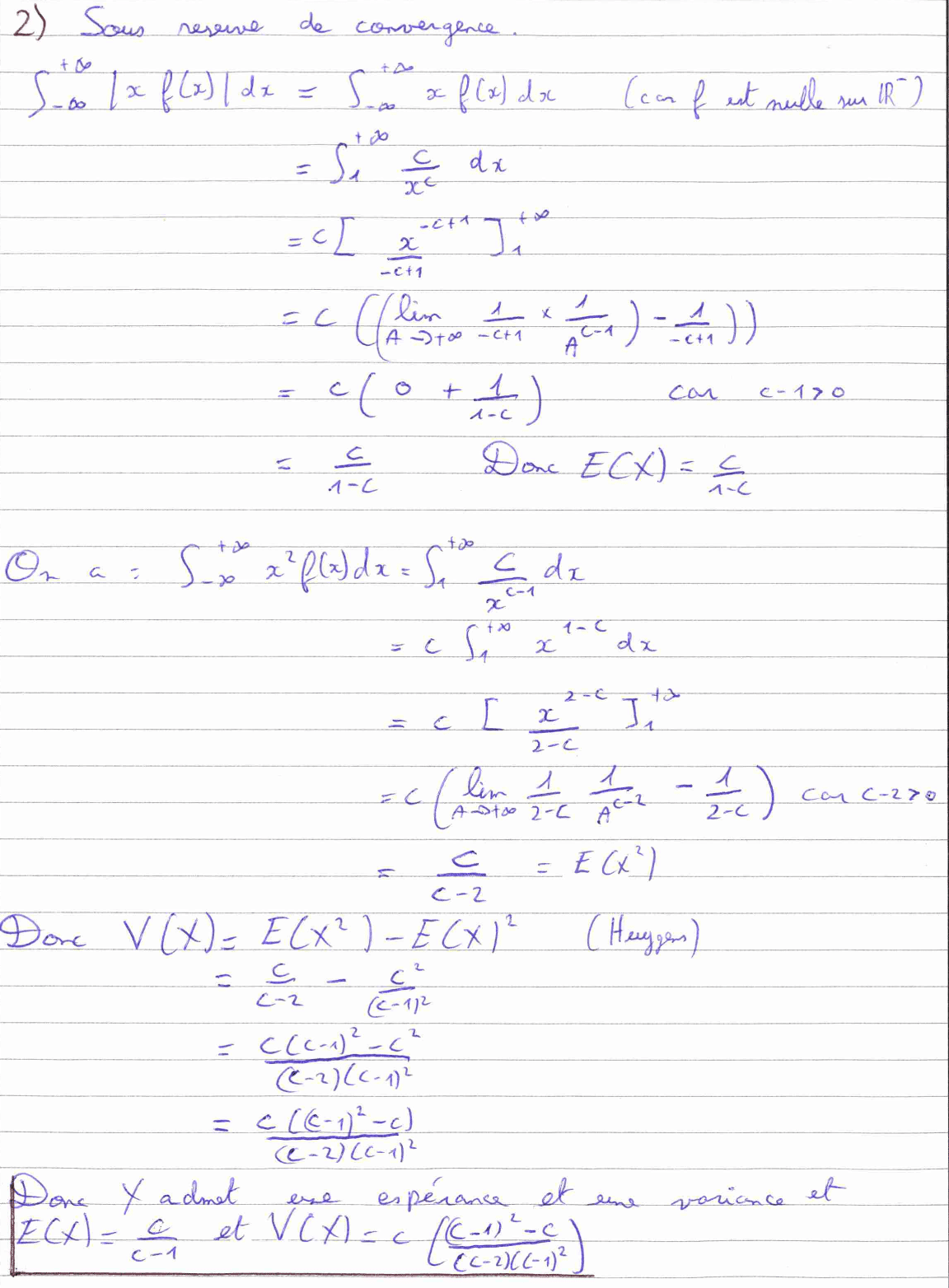
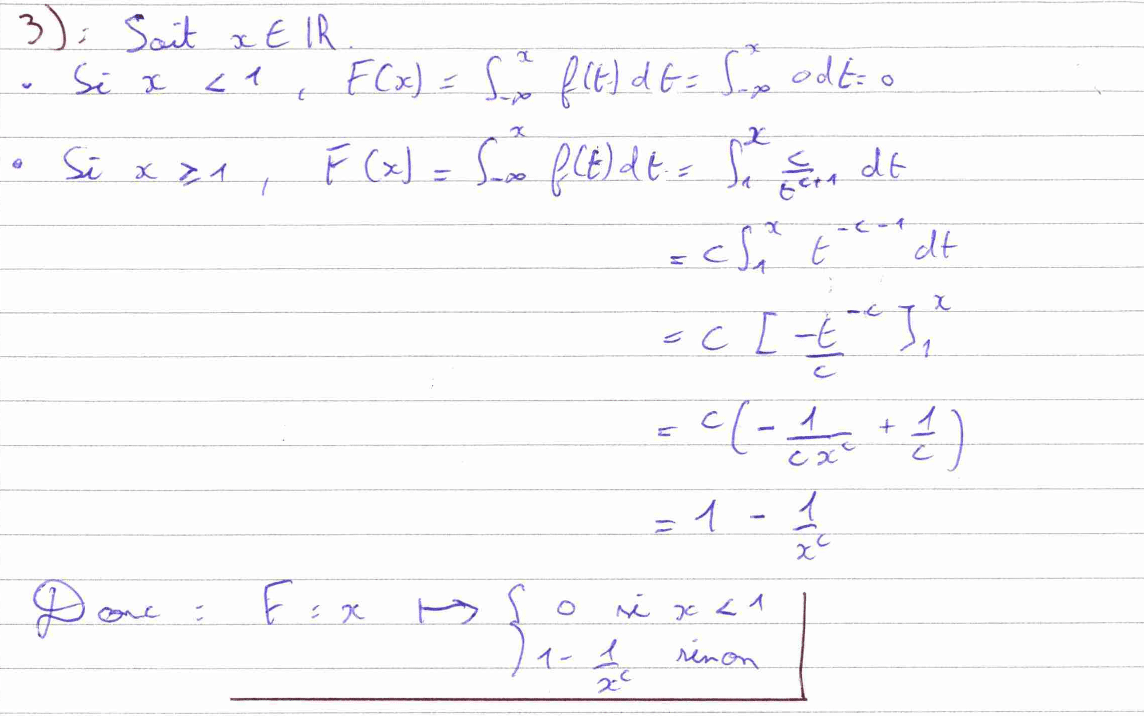
La question 4) a) nécessite d’appliquer la fonction exponentielle au sein de la probabilité. Pour cela, il est important de rappeler la croissance de la fonction exponentielle sur \(\mathbb{R}.\) La question 4) b) consiste à appliquer la définition d’une loi de Pareto qui est rappelée dans le sujet et à connaître la densité d’une variable aléatoire qui suit une loi exponentielle. La question 4) c) est la première question de Python du sujet, elle nécessite la maîtrise de la librairie Numpy et Random.


Partie II
La question 5) est aussi une question de Python qui nous fait utiliser la librairie Random et la fonction \( \text{Simul}X \) que nous venons de programmer dans la question 4) c).
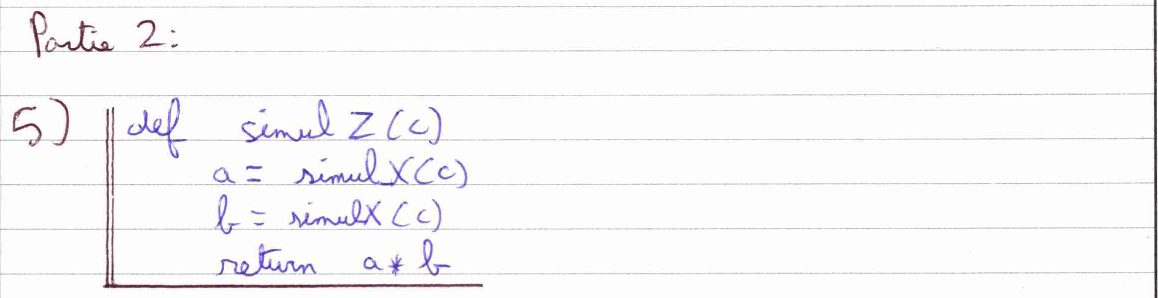
La question 6) est une question qui nécessite de nombreux calculs, elle nous fait utiliser l’indépendance de variables aléatoires. Je n’ai pas abouti au résultat attendu à 1 près. J’ai donc fait le choix de montrer cette erreur sur ma copie qui est liée à un mauvais calcul.
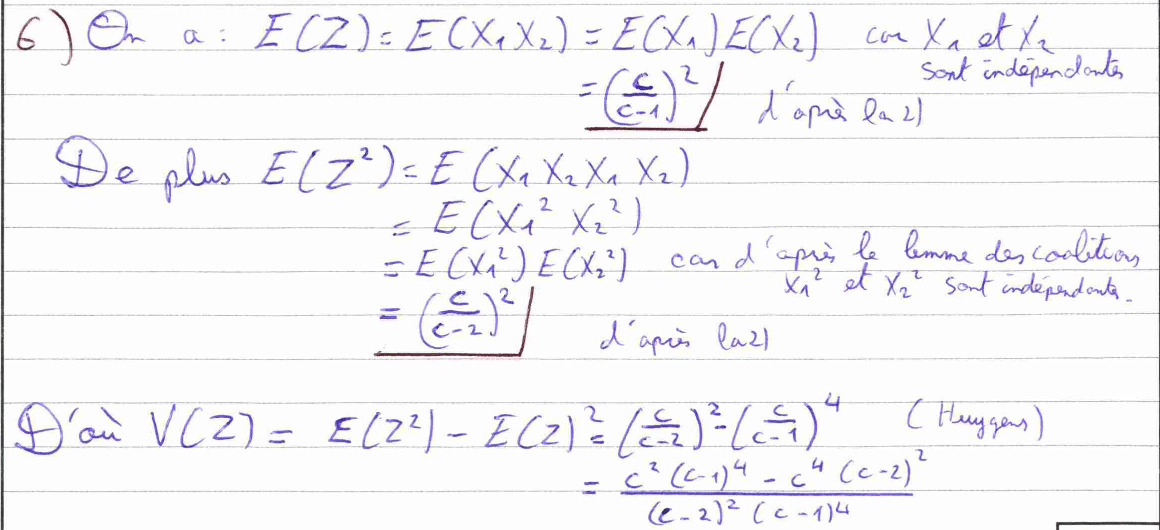
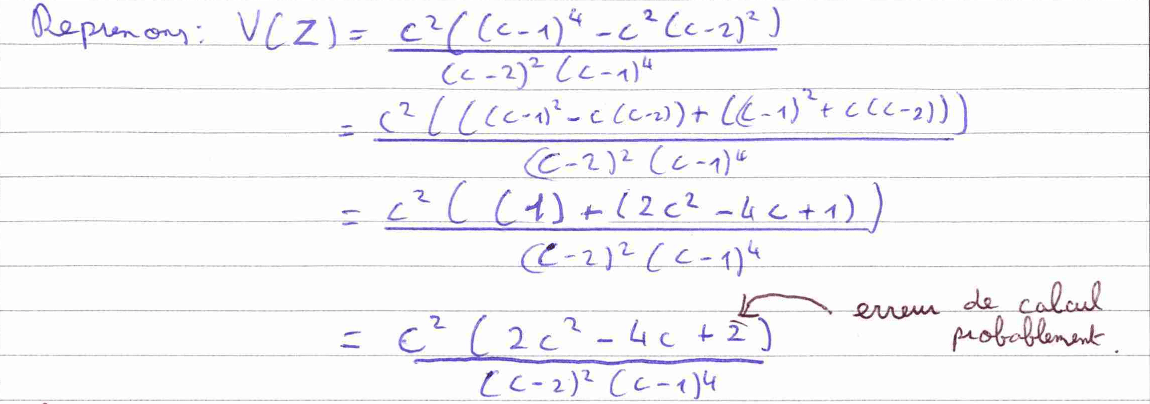
La question 7) a) est une question de cours qui vient vérifier si nous savons qu’une variable aléatoire qui suit une loi exponentielle de paramètre 1 suit une loi gamme de paramètre 1. La question 7) b) est également une question qui vient vérifier notre connaissance du cours avec le lemme des coalitions et la stabilité de la somme de variables aléatoires indépendantes qui suivent des lois gammas.

La question 8) a) nous fait calculer \(h\) en deux étapes. Premièrement, en exprimant la dérivée de \(H\) avec l’aide de \(K\), puis en utilisant le fait que \(K^{\prime}\) est une densité d’une loi Gamma de paramètre 2. La question 8) b) est également une question qui nécessite plusieurs calculs, je n’arrive pas au résultat attendu à 1 près, je le précise donc sur ma copie.

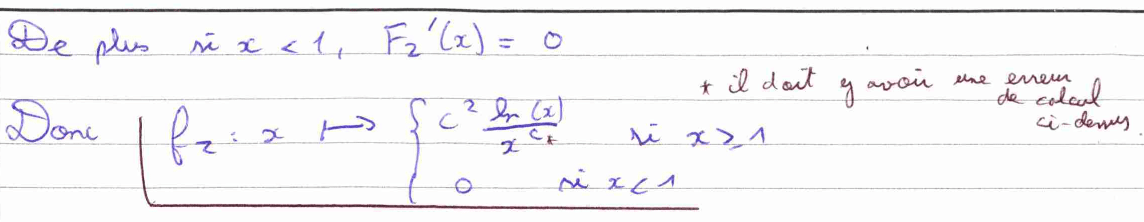
La question 9) a) est de nouveau un calcul d’une intégrale impropre qui nécessite une IPP. Il faut donc introduire \(A \in \mathbb{R^*_+} \) et ne pas directement travailler avec la borne \( + \infty.\) De même, la 9) b) consiste à calculer des intégrales en utilisant les résultats des questions 6) et 8).



Un troisième exercice de probabilités
Ce troisième est toujours sur le thème des probabilités, mais n’est plus sur la loi de Pareto. La première question est un calcul des probabilités qui nous fait étudier l’inversion d’événements et nous fait utiliser l’indépendance des lancers.
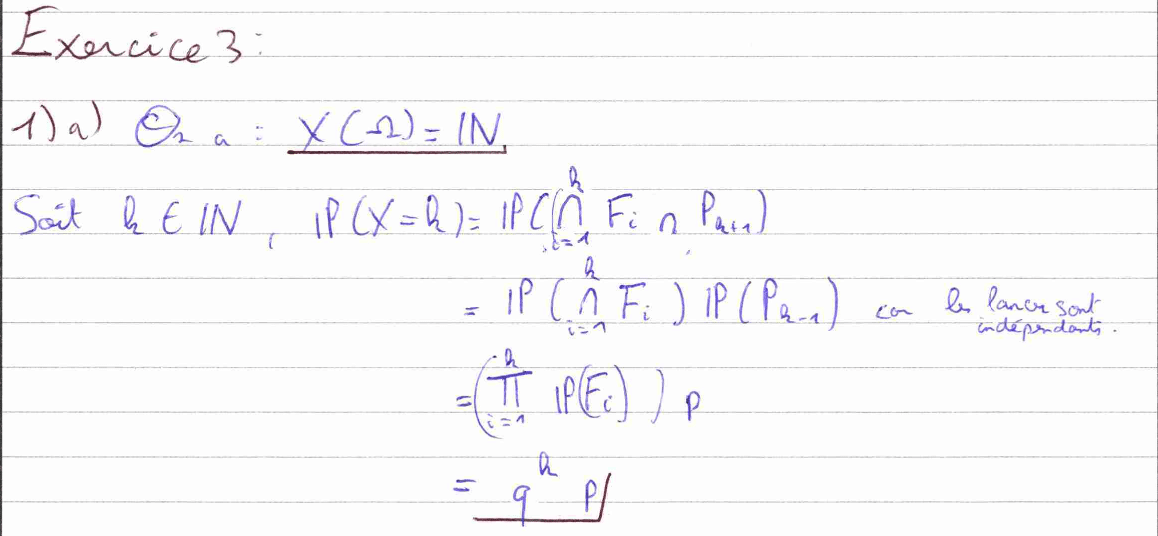
Pour la question 1) b), j’ai trouvé une astuce qui m’a fait gagner beaucoup de temps. J’ai introduit une variable aléatoire \(Y\) qui suit une loi géométrique de paramètre \(p\) et j’ai remarqué que \(X\) suit la même loi que \(Y-1\). J’ai ensuite démontré ce résultat. Finalement, nous connaissons l’espérance et la variance de \(Y\) grâce à notre cours, donc c’est aussi le cas pour \(Y-1\) et donc pour \(X.\)
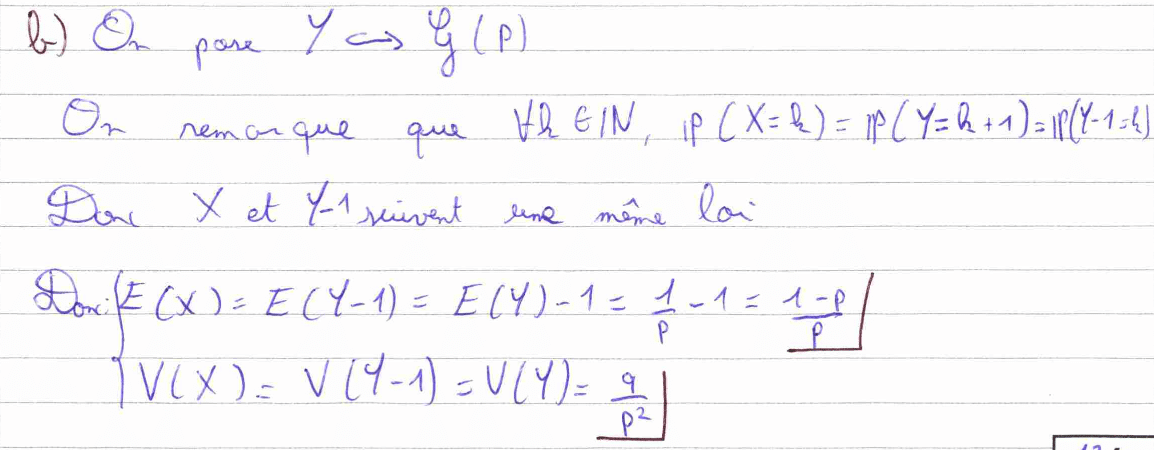
La question 2) est une question d’arithmétique, un thème peu fréquent aux concours mais qui est bien au programme. Il faut ici raisonner sur le reste dans la division euclidienne de \(X\) par 3.
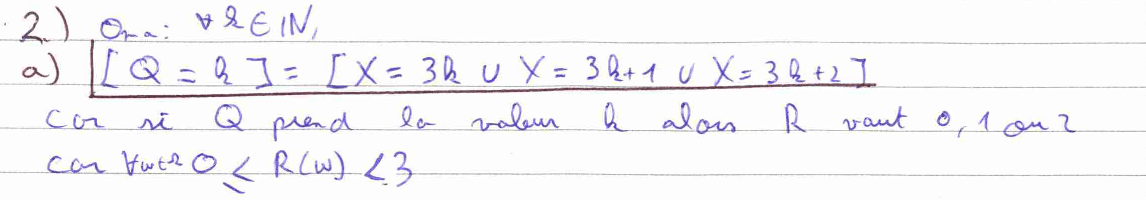
La question 3) consiste à calculer des probabilités d’unions d’une infinité d’événements en utilisant le fait que ces unions sont disjointes et en calculant des séries géométriques.
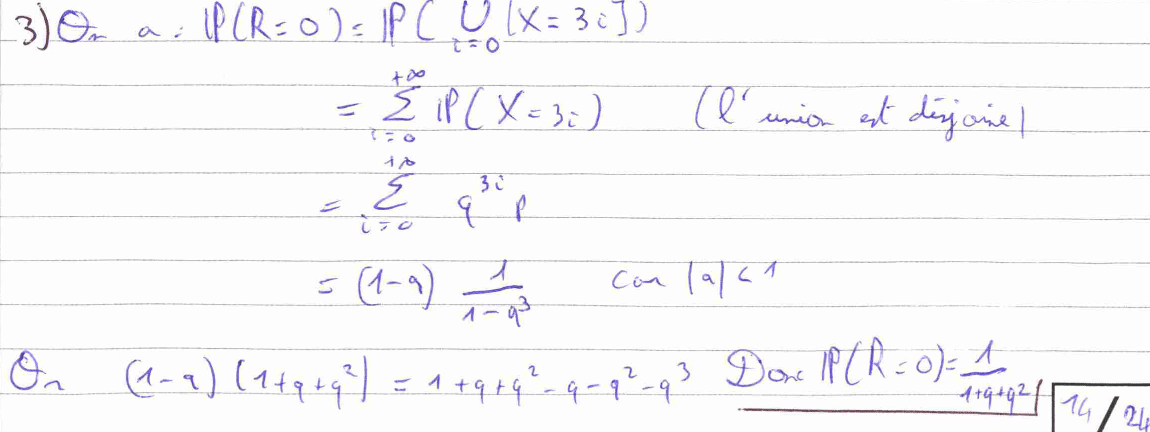
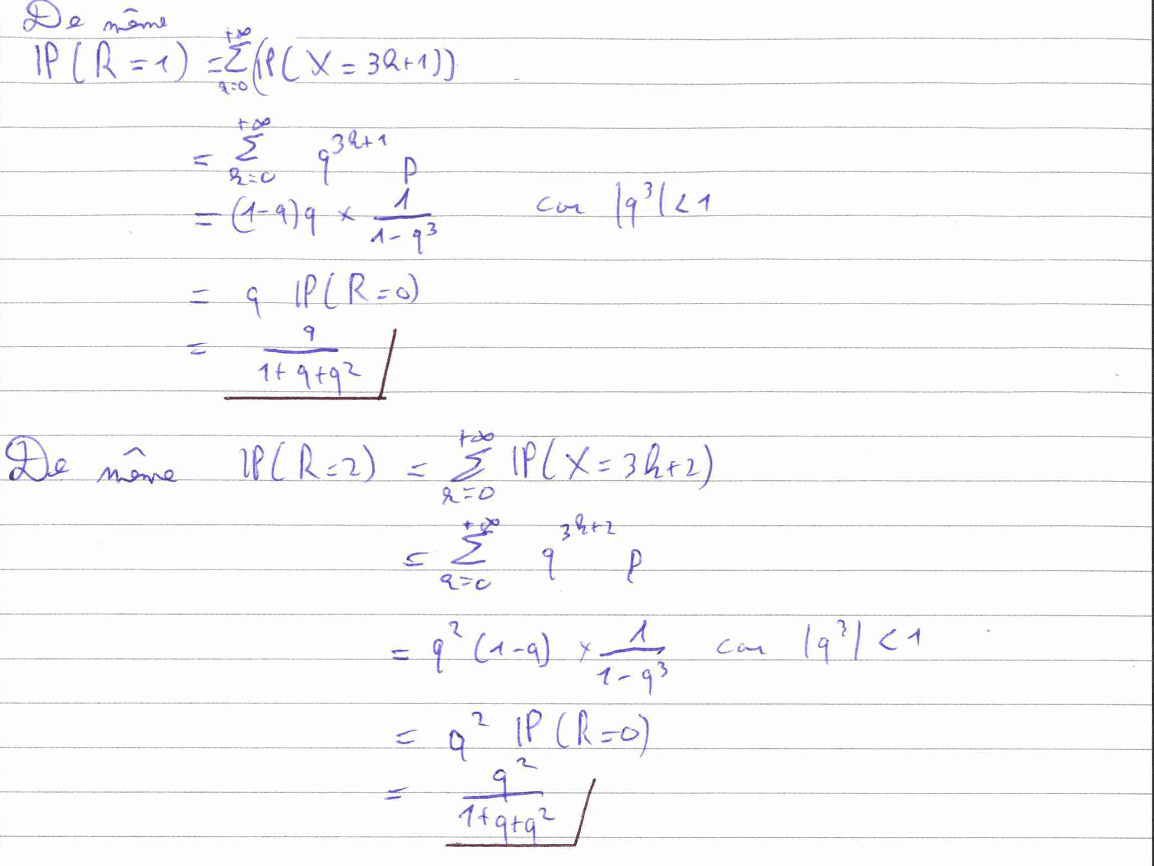
J’ai passé la question 4) et je l’ai noté sur ma copie, un geste qui peut être apprécié chez certains correcteurs. Cela montre bien qu’il n’est pas nécessaire de finir le sujet pour avoir 20/20.

La question 5) nous fait analyser un programme Python et nous fait justifier l’astuce que nous avons utilisée précédemment dans la question 1) b). Nous fournissons donc la même justification. C’est-à-dire la loi de \(X\) suit la même loi que \(Y-1\) où \(Y\) est une variable aléatoire qui suit une loi géométrique de paramètre \(p\). La question 5) b) nous demande de coder une fonction Python qui nécessite l’utilisation du symbole % qui donne le reste dans une division euclidienne.
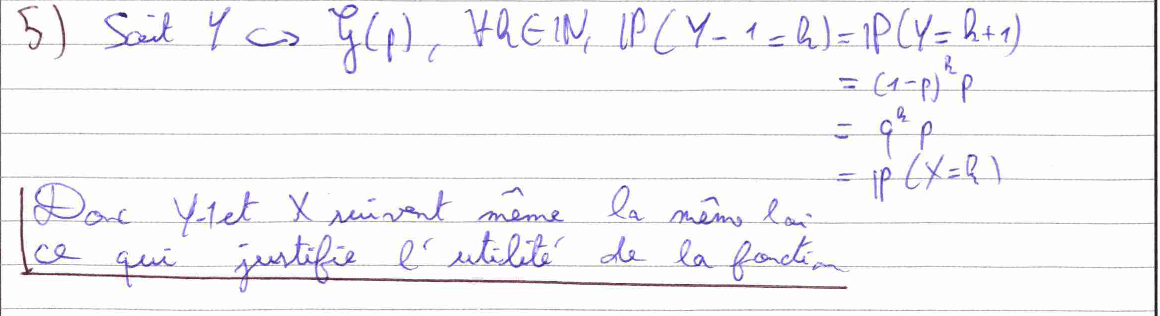
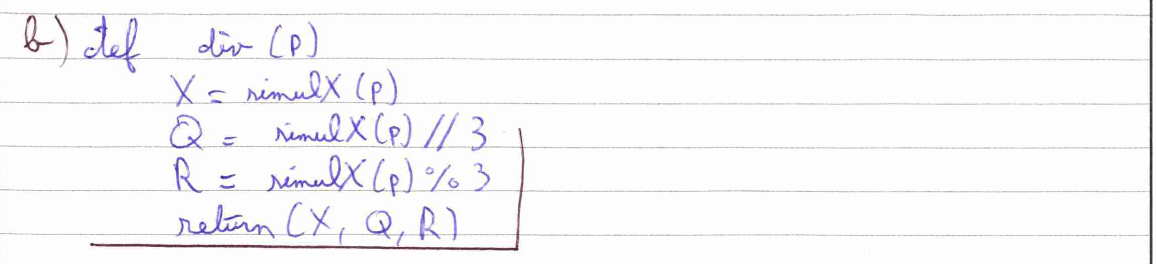
Un problème d’algèbre bilinéaire et de trigonométrie
Le sujet d’EDHEC 2023 se termine sur un problème qui a été discriminant de par ses objets d’études : la trigonométrie, l’algèbre bilinéaire et, dans une moindre mesure, l’arithmétique.
Dans la première question du problème, il faut montrer que la fonction \(k\) est \(n\text{-périodique}\). Pour cela il faut utiliser la périodicité de \( \cos.\)
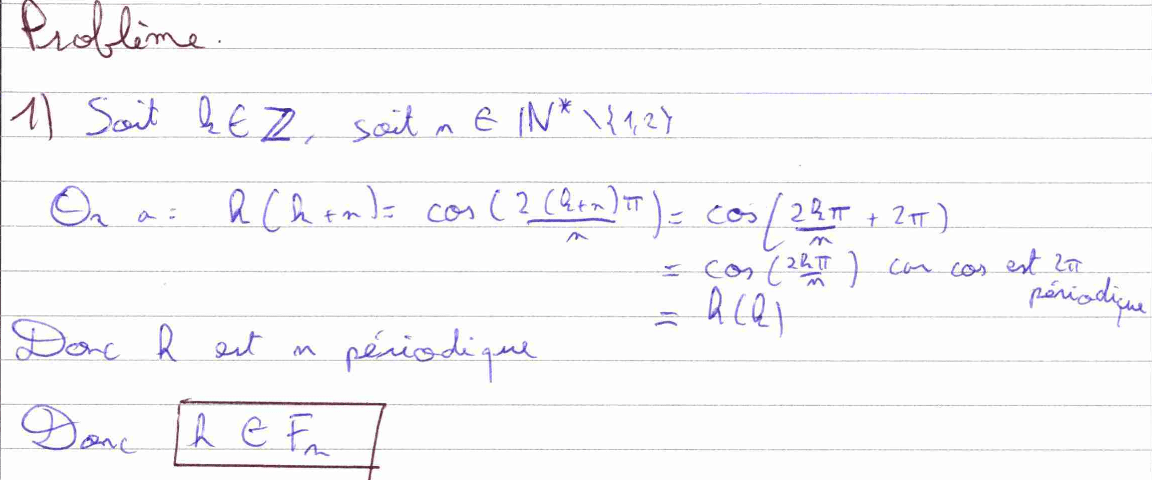
La question 2) nous fait démontrer que \(F_n\) est un espace vectoriel, nous devons utiliser la définition d’un espace vectoriel.

Dans la troisième question, pour arriver au résultat attendu, il faut utiliser l’égalité \( k = nq + r \) qui correspond à la division euclidienne de \(k\) par \(n.\)
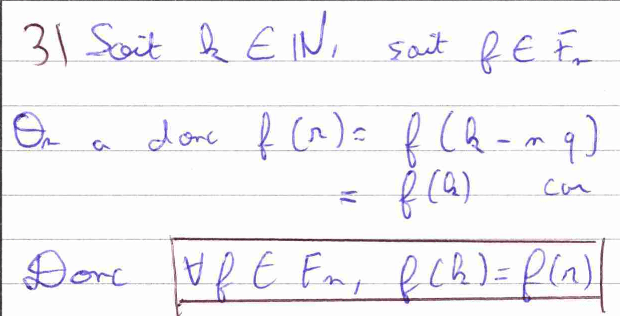
Pour la 4) a), il faut calculer la somme demandée en se servant directement de la définition des \(e_i\) qui est rappelée dans le sujet. Pour la 4) b), il faut de manière analogue utiliser la définition des \(e_i\) pour montrer la liberté de la famille indiquée. De plus, en se servant de la 4) a), on arrive à montrer que cette famille est génératrice de \(F_n\). Nous pouvons donc affirmer que c’est une base de \(F_n.\) La 4) c) nous fait simplement commenter l’égalité de la 4) a).
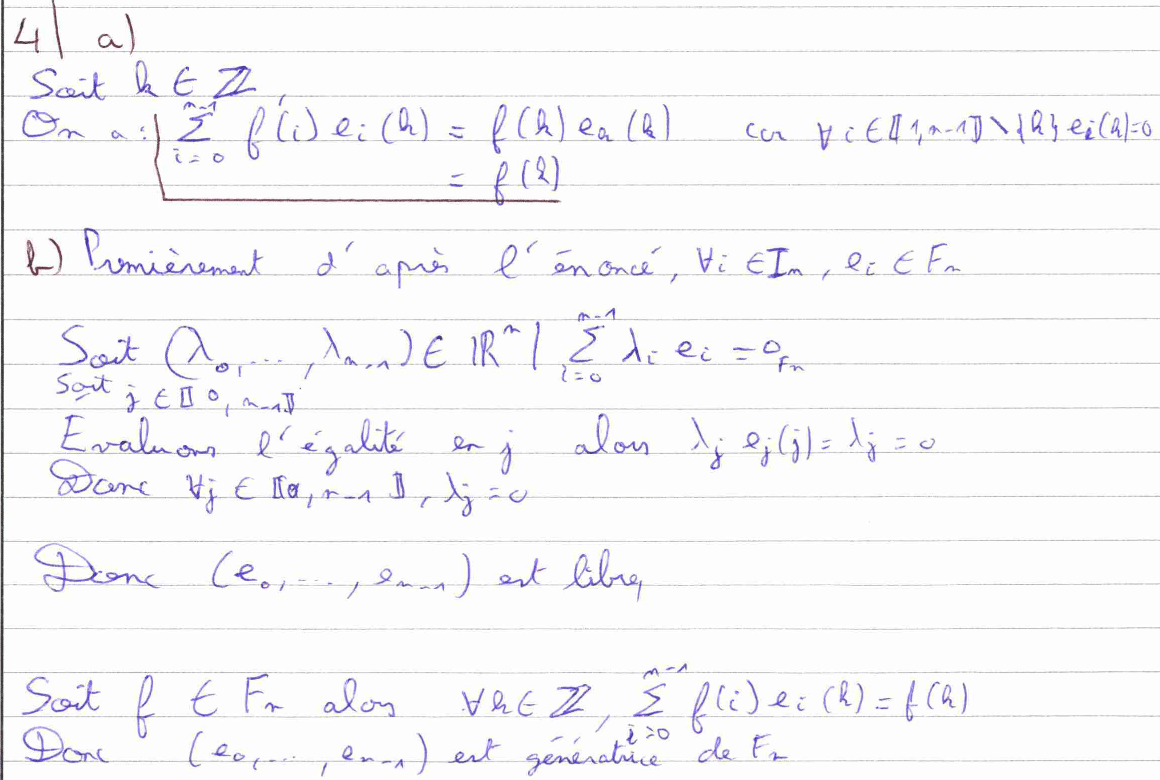

La question 5) a) consiste à montrer qu’une certaine application est un produit scalaire. Une question facile lorsqu’on connaît les différentes étapes. Cependant, il est important de soigner sa rédaction sur ce genre de questions. La question 5) b) nous fait une fois de plus utiliser la définition des \(e_i,\). D’où l’importance de prendre un moment pour correctement comprendre les objets mathématiques introduits dans un sujet.


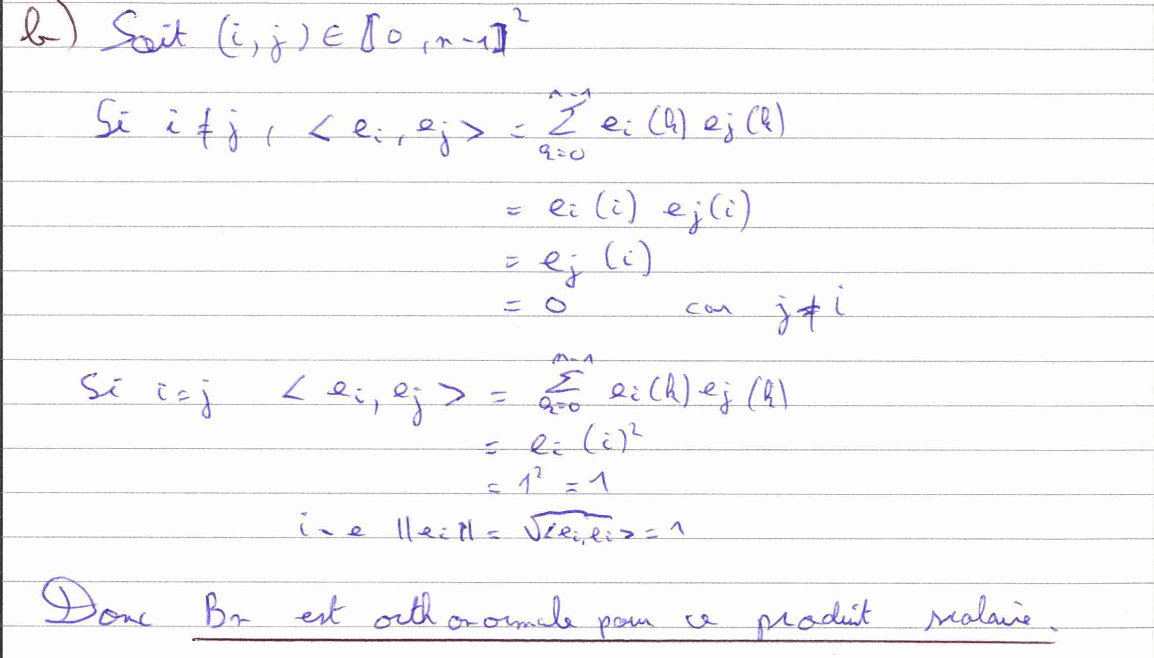
La question 5) c) est davantage technique, car elle nécessite d’utiliser une formule trigonométrique (rappelée dans le sujet) au sein d’une somme télescopique. Quant à la 5) d), c’est une application directe du résultat de la 5) c) qui nous demande aussi d’utiliser une valeur particulière de la fonction sinus. La question 5) e) est un résumé des questions qui précèdent, il faut partir de la définition d’une norme et calculer astucieusement une somme en servant du résultat de la 5) d). Cela montre bien l’importance d’admettre et de comprendre les résultats précédents.
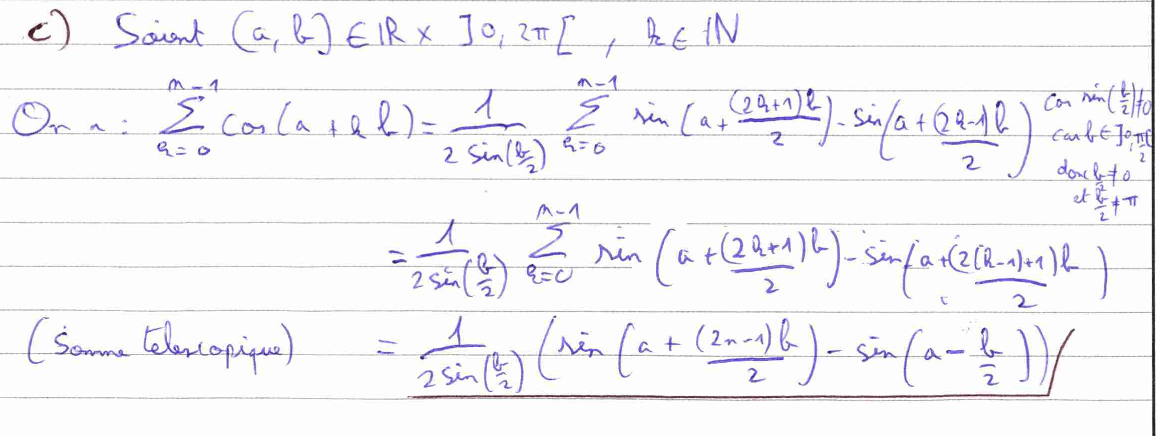
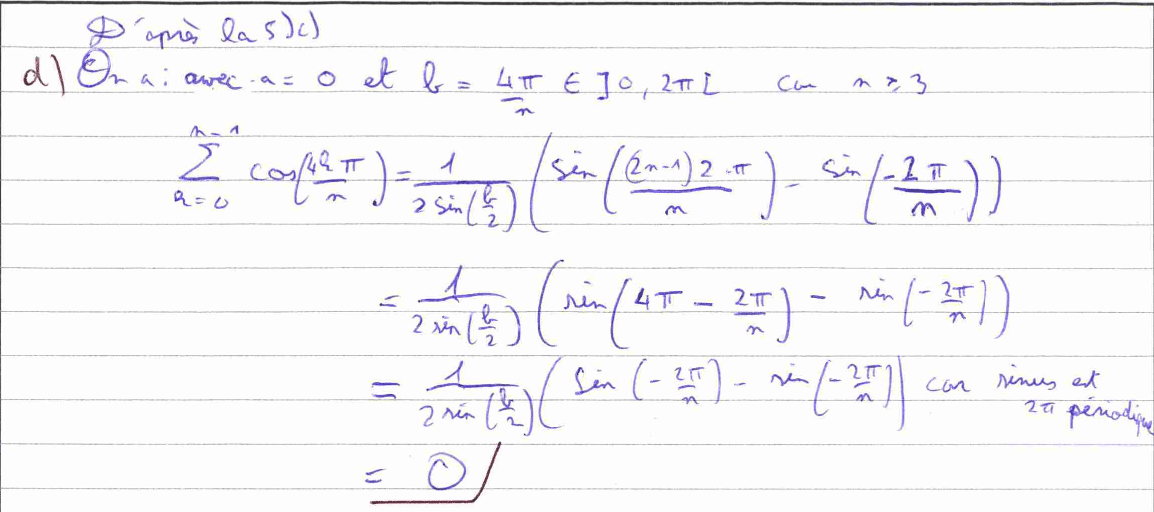
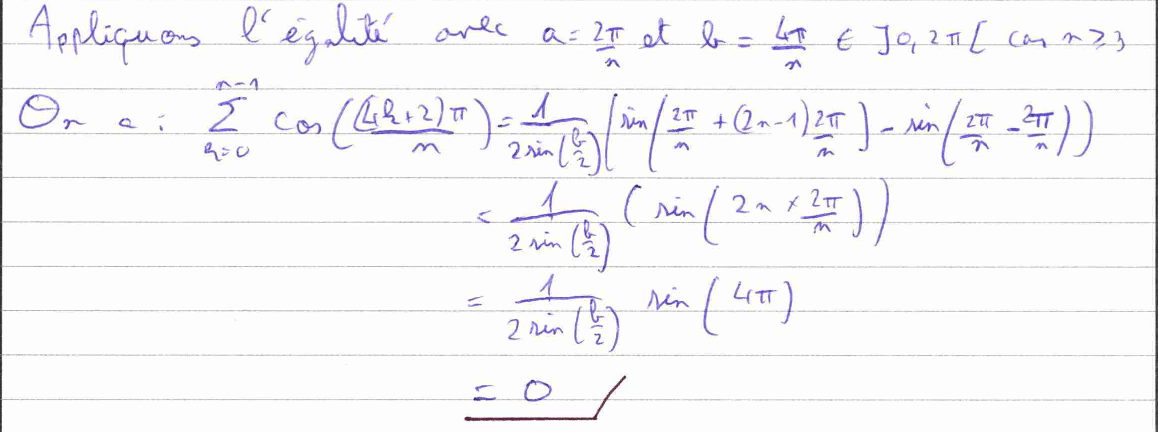
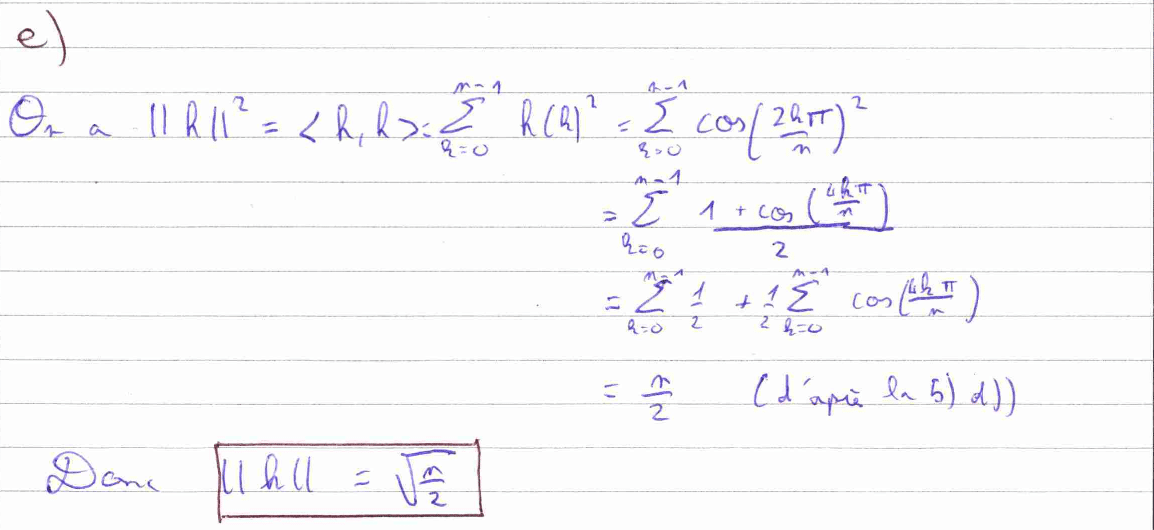
La question 6) a) nous fait utiliser des définitions qui sont rappelées dans le sujet. La définition d’un élément de \(F_n\) et la définition de l’application \(D_f.\) Quant à la 6) b), il faut montrer que \(D\) est un endomorphisme de \(F_n,\). Pour cela, il faut montrer que \(D\) est une application linéaire et que \(D\) est à valeurs dans \(F_n.\)
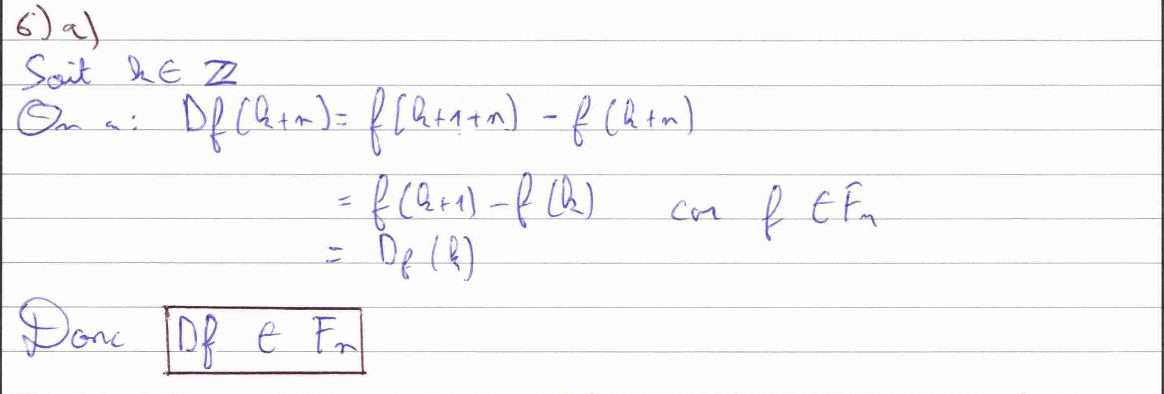
La question 6) c) consiste à montrer une égalité. Cela se fait en utilisant une formule trigonométrique (rappelée dans l’énoncé). Pour calculer la somme demandée dans la question 6) d), il faut utiliser une formule trigonométrique (rappelée dans l’énoncé) et utiliser le résultat de la question 5) d).

La question 7) a) demande de montrer une égalité. Pour cela, il faudra calculer chaque membre séparément, ce qui nécessite de longs calculs de sommes où il sera important de faire des changements d’indices. La 7) b) est une application directe du cours où il faut utiliser la définition d’un endomorphisme symétrique. Quant à la 7) c), il faut utiliser la définition d’un vecteur propre et le résultat de la question 7) a) pour montrer que toutes les valeurs propres de \(\Delta\) sont inférieures ou égales à 0.
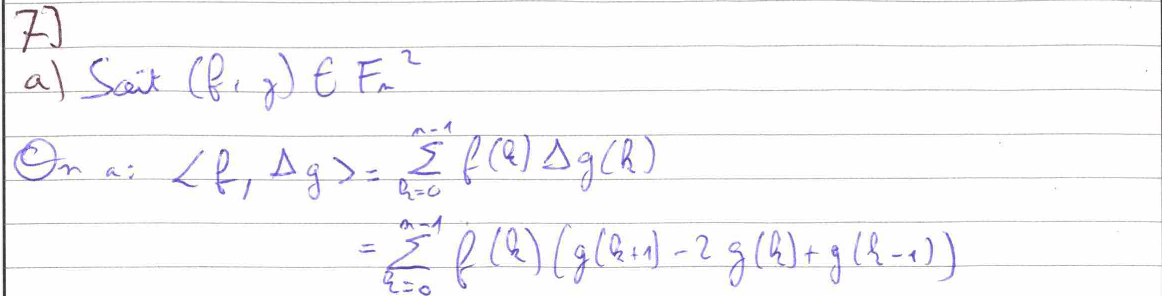
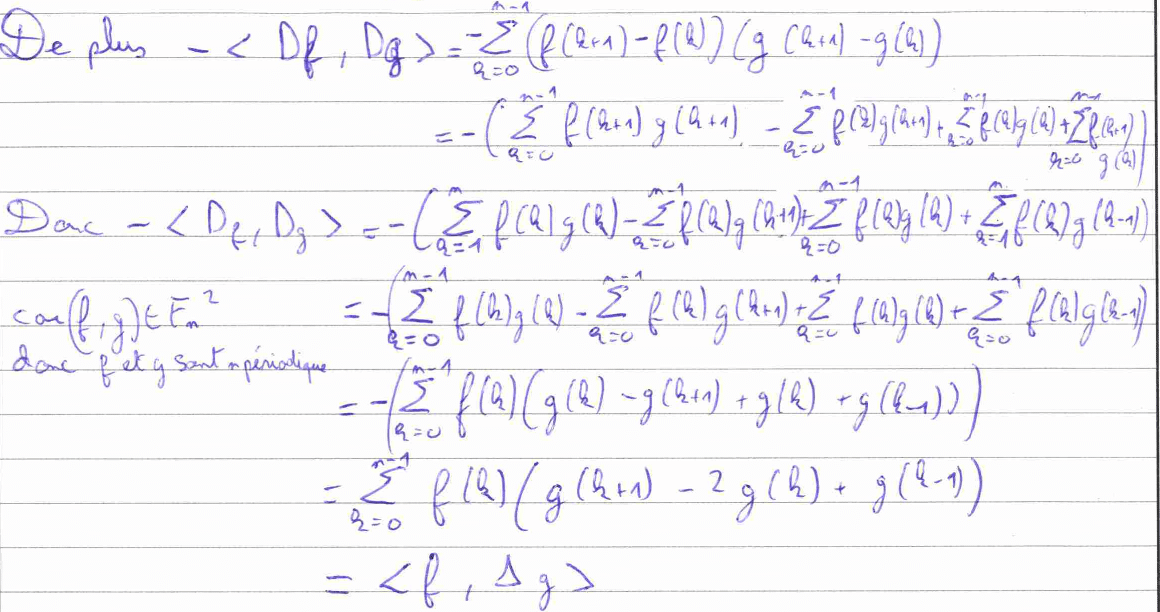
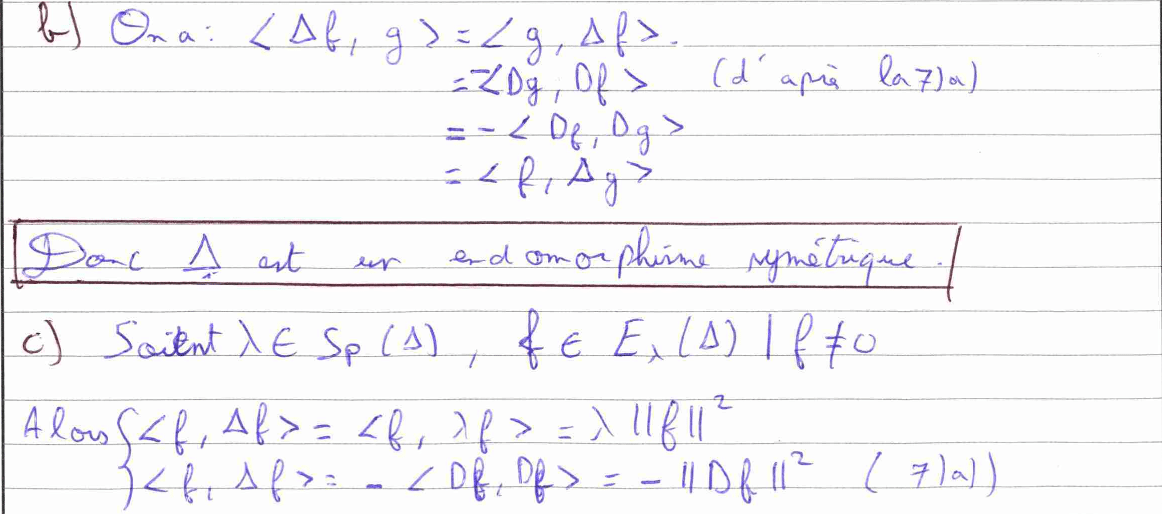

La question 8) a) nous fait appliquer directement la définition des \( \epsilon_i \) introduite pour cette question. La 8) b) est davantage technique et je ne l’ai pas terminée. J’ai donc proposé un début de raisonnement et expliqué ce qu’il manquait pour arriver au résultat attendu.

La question 9) a) est la dernière question que j’ai traitée dans ce sujet. Cela montre une fois de plus qu’il n’est pas nécessaire de finir un sujet pour avoir 20/20. Pour montrer le résultat de cette question, il faut utiliser le fait que \(D\) est symétrique donc diagonalisable et le fait que \(f\) est un élément de \(F_n.\) Nous pouvons noter que les dernières questions du sujet (10) a), 10) b) et 10) c)) sont des questions d’applications et non des questions générales. Elles sont relativement simples en comparaison aux questions que nous venons de traiter. Il aurait pu être intéressant pour certains candidats d’aller y chercher des points. Dans mon cas, j’ai manqué de temps pour les aborder.

Conclusion
Cet article visait à partager mes méthodes et astuces sur l’épreuve de mathématiques approfondies EDHEC, où j’ai obtenu la note de 20/20. À travers les commentaires détaillés, les points positifs et négatifs de ma copie, mon intention était de mettre en lumière les stratégies, les méthodes de rédaction et la préparation rigoureuse qui m’ont aidé à exceller dans cette épreuve et qui pourraient aussi t’aider à obtenir une très bonne note.
Les exercices abordés, qu’ils traitent d’algèbre linéaire, de probabilités, ou de trigonométrie, illustrent l’importance d’une compréhension profonde des concepts, d’une rédaction précise et de la capacité à appliquer des méthodes de résolution efficaces. Les questions de Python soulignent également l’importance de la programmation dans les sujets de concours.
J’espère que le partage de mon expérience et de mes méthodes pourra te guider dans ta préparation aux épreuves de concours.
N’hésite pas à consulter toutes nos autres ressources mathématiques !