L’épreuve de mathématiques approfondies de HEC est souvent considérée comme l’une des plus redoutables. En effet, elle frôle le hors-programme et nécessite des raisonnements complexes, mais elle peut être maîtrisée avec dévouement et persévérance. Dans cet article, nous analyserons ma copie de Maths I HEC de 2023 notée 19,68/20 en découvrant les méthodes et les astuces qui ont conduit à ce résultat. Mon objectif est ainsi de te montrer ce qui m’a permis d’avoir une telle note, en soulignant question par question tous les points positifs et négatifs de ma copie.
Présentation de l’épreuve
Les deux épreuves de mathématiques de HEC sont réputées comme particulièrement difficiles. Elles testent la capacité des candidats à développer des raisonnements complexes sur des notions qu’ils n’ont pas nécessairement étudiées en classe. Parmi ces deux épreuves, le Maths I se distingue du Maths II par ses questions qui portent généralement sur l’algèbre linéaire et moins sur les statistiques et les probabilités.
Ce fut ainsi une surprise et une déception personnelle de voir que l’objet du problème portait sur des probabilités et non sur de l’algèbre linéaire ou bilinéaire. Cependant, face à un sujet déconcertant et inhabituel, il ne faut pas se laisser abattre et avoir confiance en sa préparation. En effet, si un sujet te paraît inhabituel, c’est probablement aussi le cas pour les autres candidats.
Le sujet Maths I de 2023 est divisé en trois parties qui nous permettent de travailler sur un problème du domaine des probabilités. Ce problème est le célèbre problème des moments qui consiste pour une certaine suite \( (u_k)_{k \in \mathbb{N}} \) à trouver une variable aléatoire réelle \(X\) qui admet pour moments d’ordres les termes de la suite \(u\) et qui admet une densité \(f\) continue sur un intervalle \(J\) de \( \mathbb{R}.\) La deuxième partie se concentre sur le cas où \(J=\mathbb{R_+^*}\) et la troisième partie sur le cas où \(J=[0,1].\)
Les premières questions : mettre l’accent sur la rédaction
La première question de ma copie a été l’opportunité de montrer au correcteur que je savais faire preuve de rigueur en termes de rédaction. C’est ce que j’ai voulu montrer avec l’introduction des variables précédées du mot « Soit », en précisant « Sous réserve de convergence » pour le calcul de l’intégrale, en indiquant le théorème que j’utilise et en encadrant le résultat final.

J’ai continué sur cette lancée pour la deuxième et dernière question de cette première partie en justifiant correctement le changement de variable. J’ai aussi pu gagner du temps en reconnaissant la fonction Gamma dans l’intégrale plutôt que de recalculer sa valeur à l’aide d’une IPP.
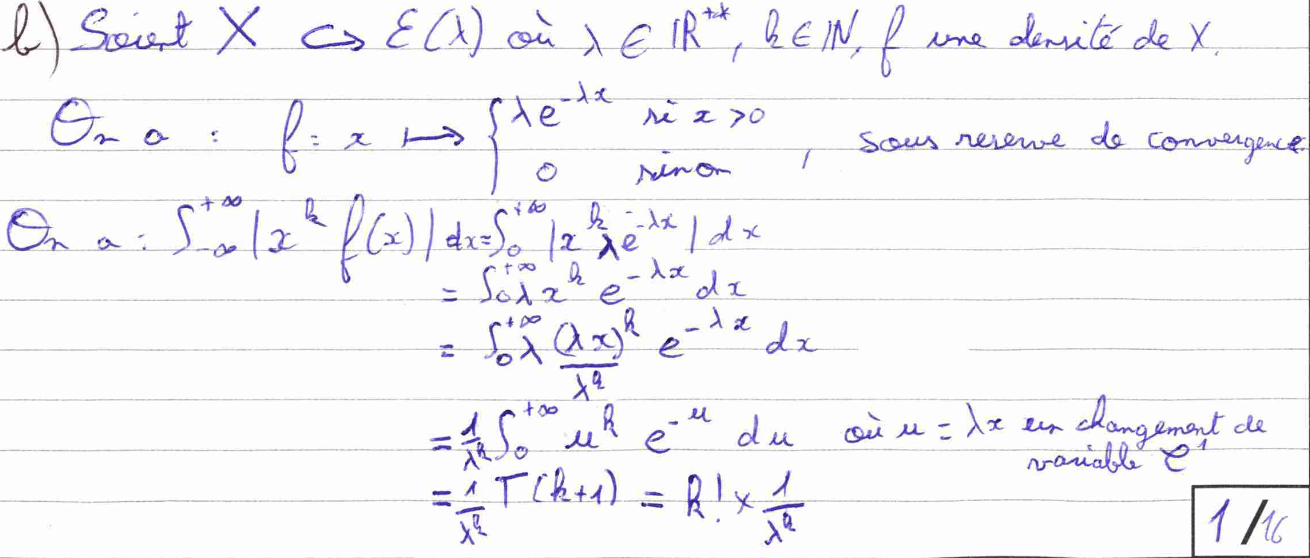

Une deuxième partie plus compliquée : gérer l’échec
La deuxième partie du sujet nous fait étudier le problème des moments dans le cas où \(J=[0,1]\) et les deux premières questions nécessitent simplement de faire preuve de rigueur dans le calcul et d’un usage malin du théorème de transfert en remarquant que \( \forall x \notin J, f(x)=0.\)
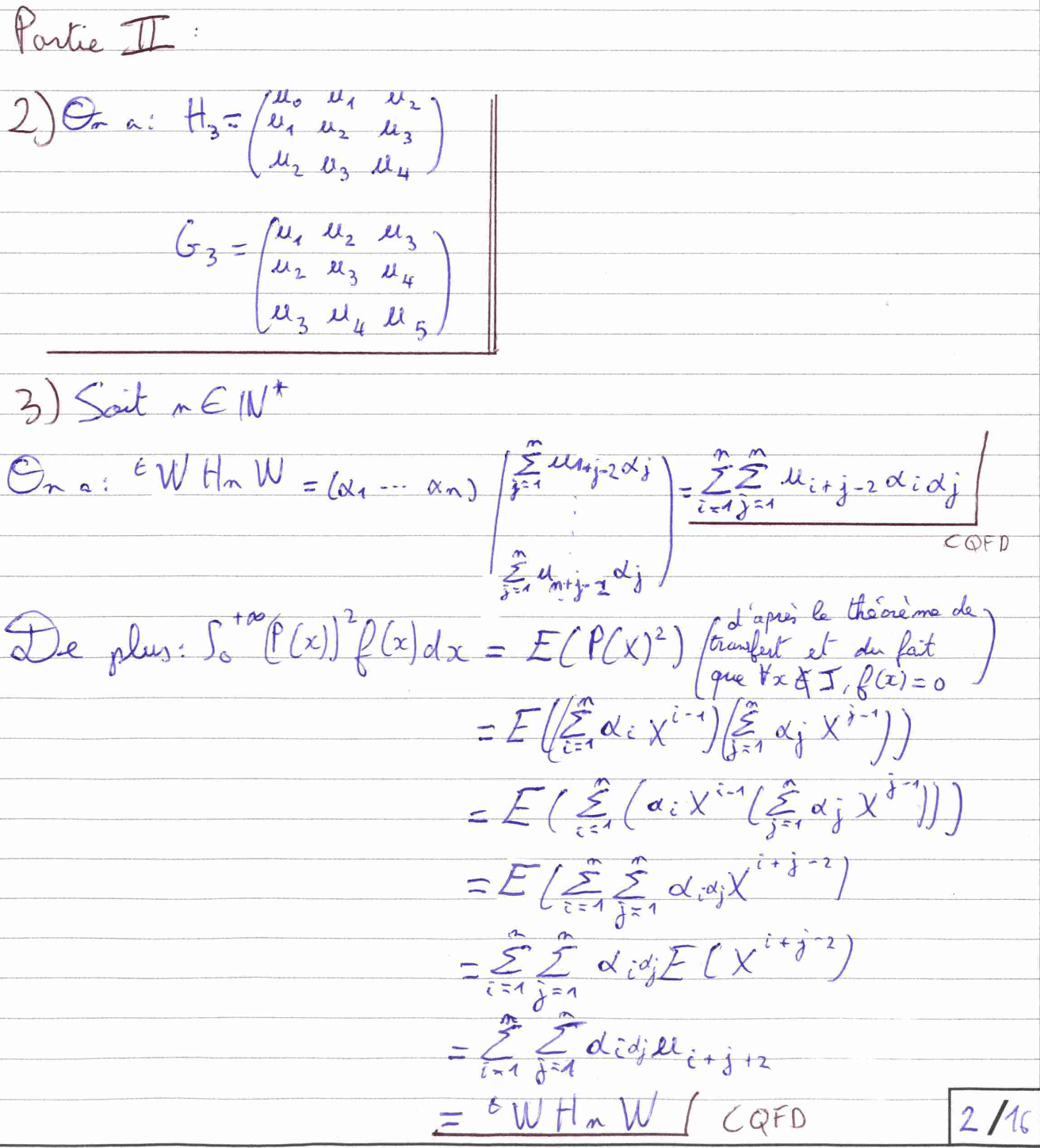
La quatrième question n’est pas plus compliquée, mais il faut cependant justifier l’existence d’une valeur propre de \(H_n\) en utilisant le théorème spectral et la symétrie de la matrice. Ce genre de détails peut paraître anodin, mais ils sont essentiels car, sans cette précision, nous ne savons pas si l’objet avec lequel nous travaillons existe.

Nous arrivons à un moment difficile où les questions commencent à se corser. Les questions 5, 6 et 7a m’ont pris de court et je n’ai pas réussi à en traiter une jusqu’au bout… Ça a été un moment difficile moralement, car nous ne sommes encore qu’au début du sujet et ça s’annonçait compliqué pour la suite. Cela montre bien qu’il n’est pas nécessaire de finir le sujet pour avoir une bonne note. Il était cependant impératif de rebondir suite à ces premiers échecs.

La question 8 qui est la dernière question de la première sous-partie de la deuxième partie est la première question de Python du sujet. Elle est donc synonyme de points potentiellement faciles à gagner. J’ai pris l’initiative de recopier le script en entier et j’ai fait une erreur qui a dû me coûter une partie des points. À la huitième ligne, c’est « m » et non « m-1 » et à la douzième ligne aussi.
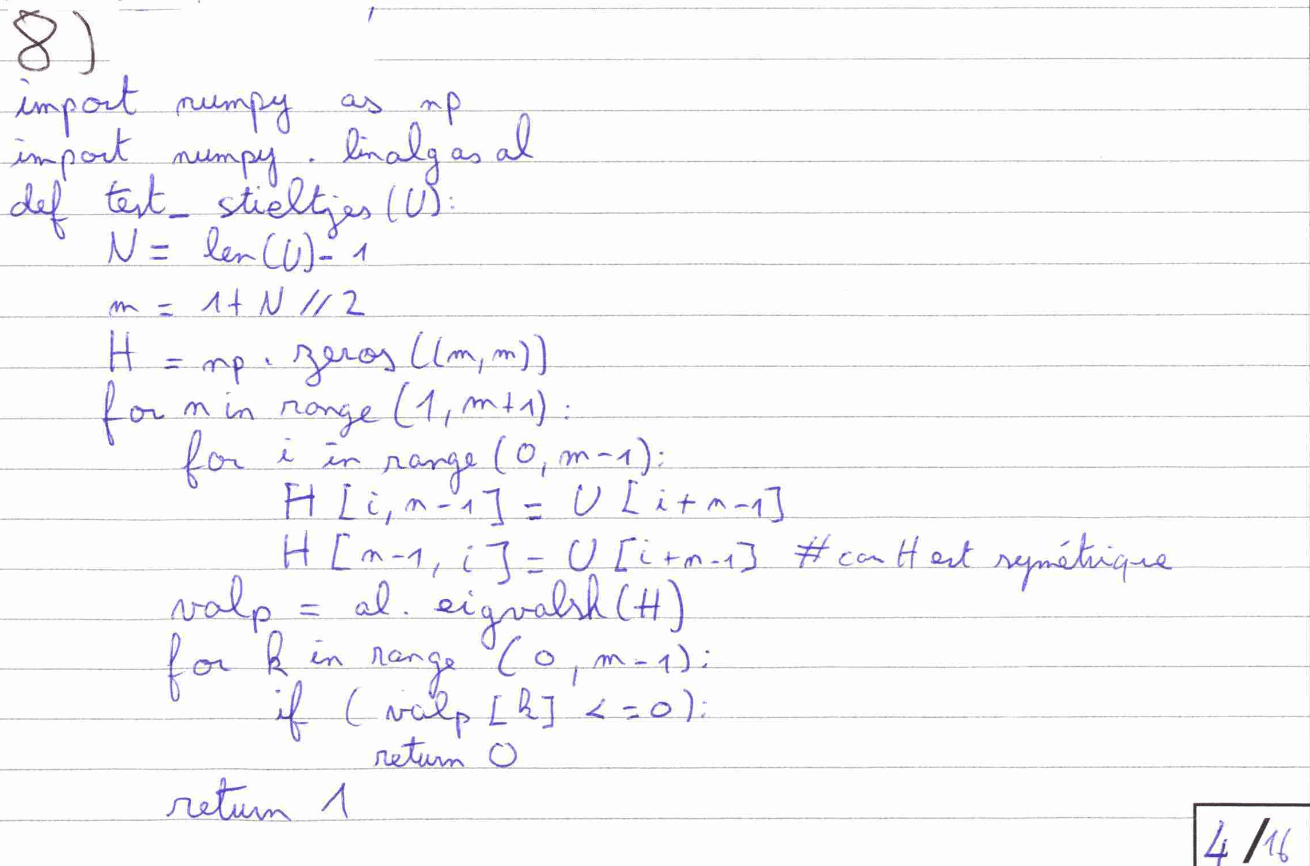
Une deuxième sous-partie pour rebondir
La deuxième sous-partie de la partie II était l’occasion de me rattraper et j’ai pu saisir cette opportunité en répondant correctement à huit questions sur les neuf qui composent cette sous-partie. Ainsi, même si le début de sujet te paraît complexe, il ne faut pas baisser les bras et continuer à aller chercher des points plus loin.
La question 9 nous fait démontrer la convergence (donc l’existence) de deux intégrales. J’ai pu gagner du temps en reconnaissant un moment d’ordre \(n\) d’une loi exponentielle.
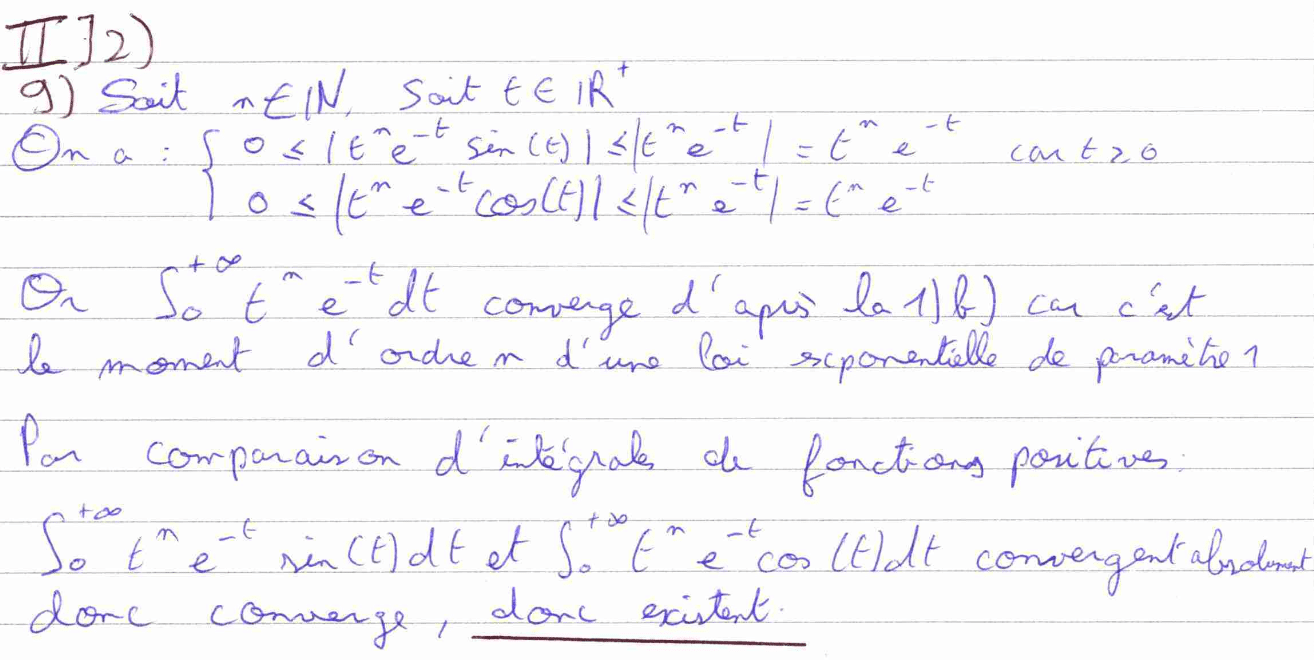
La question 10 est un calcul d’intégrale à l’aide d’une double IPP et du théorème des gendarmes. Il est donc impératif de préciser que nous travaillons avec des fonctions de classe \(C^1\) et de ne pas faire notre IPP avec \(+\infty\) sur une des bornes mais d’introduire un \(A\) dans \( \mathbb{R}_+^*.\)
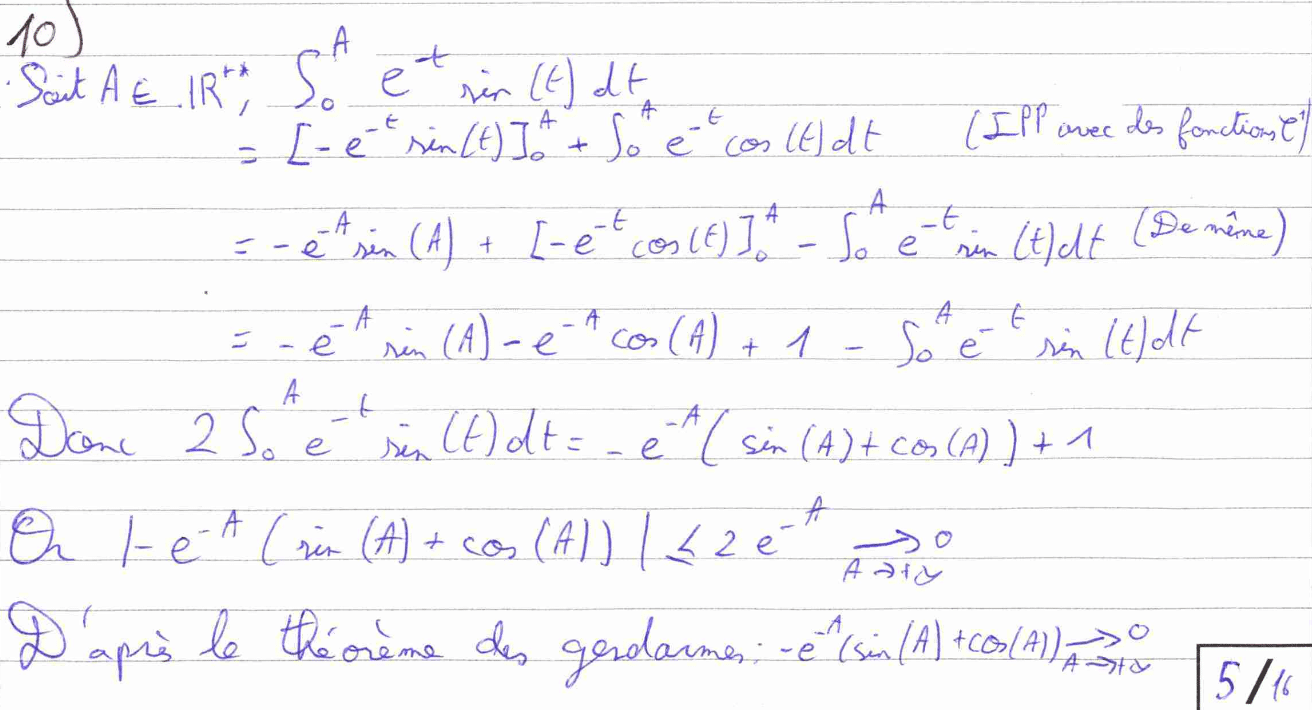

La question 11 est un exemple intéressant de comment nous pouvons gagner du temps en rédaction. Cette question nous demande de montrer deux résultats très similaires. Ainsi, nous pouvons préciser (dans une certaine mesure) « comme ci-dessus » dans la seconde démonstration à condition que la première ait été rédigée de manière irréprochable.
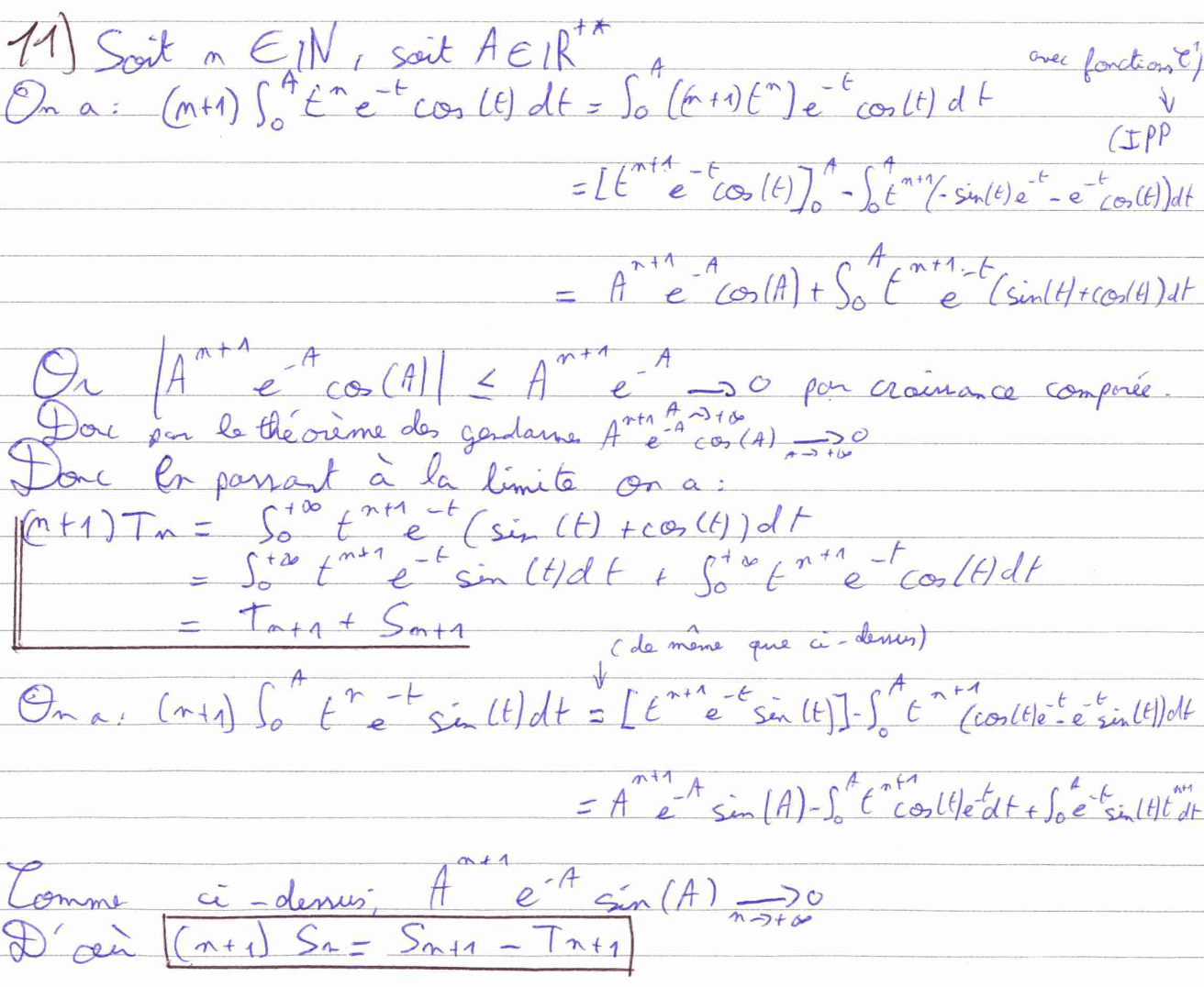
La question 12 ne présente pas de difficultés particulières, car c’est simplement un calcul matriciel. Il faut cependant penser à utiliser le résultat de la question 11 que nous venons de démontrer.
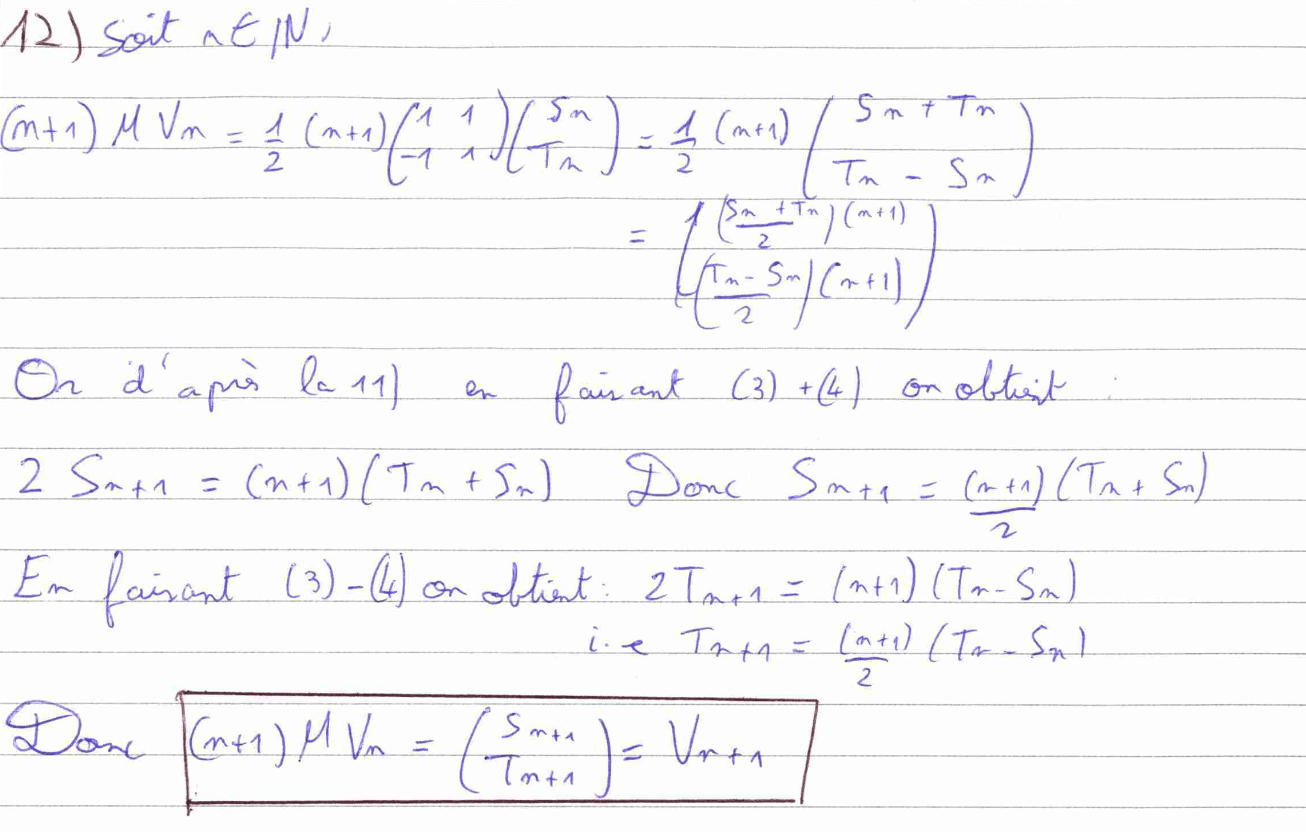
Pour la question 13, je me suis permis de faire une récurrence immédiate pour gagner du temps. Ce genre de récurrence ne s’utilise qu’à deux conditions : il faut que l’hérédité de la récurrence nécessite peu de calculs et que le début de ta copie soit irréprochable en termes de rédaction.
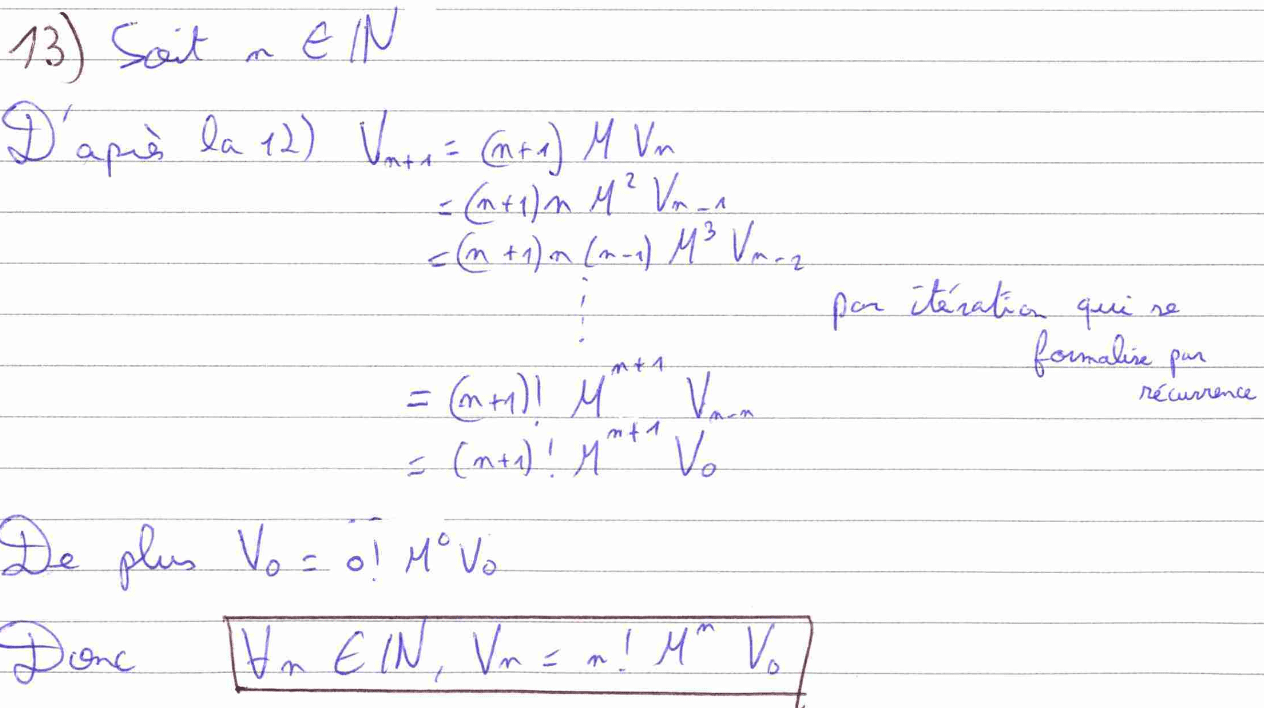
Les questions 14 et 15 ne présentent pas de difficultés particulières, il faut simplement faire preuve de rigueur dans le calcul matriciel et justifier correctement le changement de variable en invoquant la bijectivité de la fonction utilisée et sa classe \(C^1.\) J’ai cependant passé la question 16 et j’ai bien précisé que nous admettions le résultat de cette question.
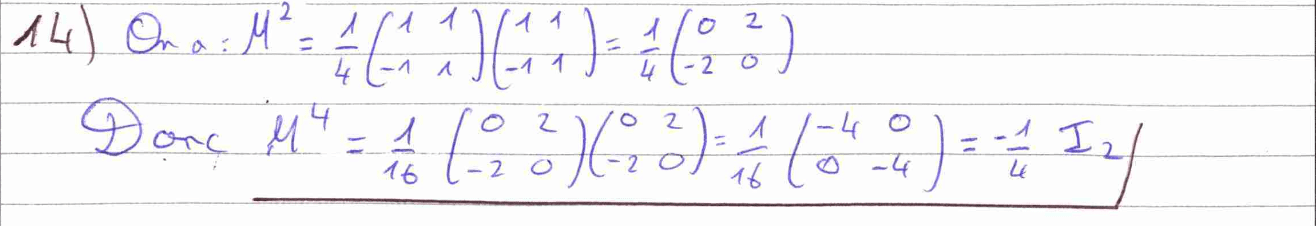

La question 17 est selon moi l’une des plus dures du sujet, car il faut comprendre ce qu’attend de nous le sujet (ici, la non-unicité de la solution) et car elle nécessite beaucoup d’initiative. En effet, il fallait penser à introduire deux densités \( G_1 \; \text{et} \; G_2 \) et montrer que les variables aléatoires qui leur sont associées sont distinctes tout en étant solutions du problème.

Une troisième partie qui nécessite de la vitesse
La troisième et dernière partie qui traite du problème dans le cas \(J=[0,1]\) du sujet est particulièrement longue et est composée de quatre sous-parties d’une difficulté croissante.
Il faut bien comprendre, dans la question 18, que nous voulons montrer la stricte positivité de \(u\) et non simplement sa positivité qui serait directe. J’ai ainsi utilisé un raisonnement par l’absurde qui utilise les propriétés de \(f\) sur \(J.\)
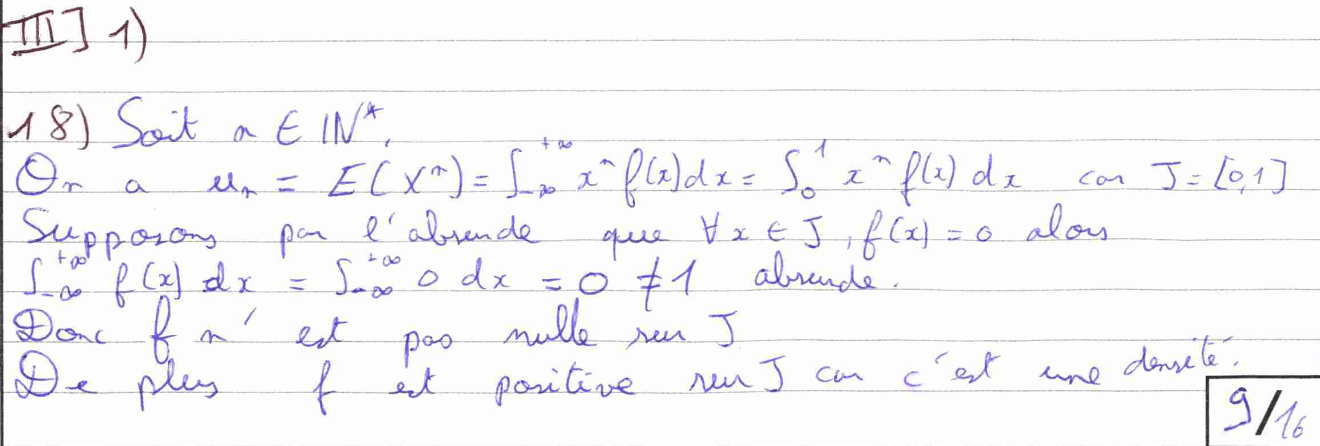
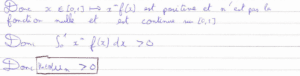
Les questions 19 et 20 nécessitent de la rigueur dans les calculs et aussi des justifications précises telles que la linéarité de l’espérance, l’utilisation du binôme de Newton et le fait que \(X\) est une variable aléatoire à densité.
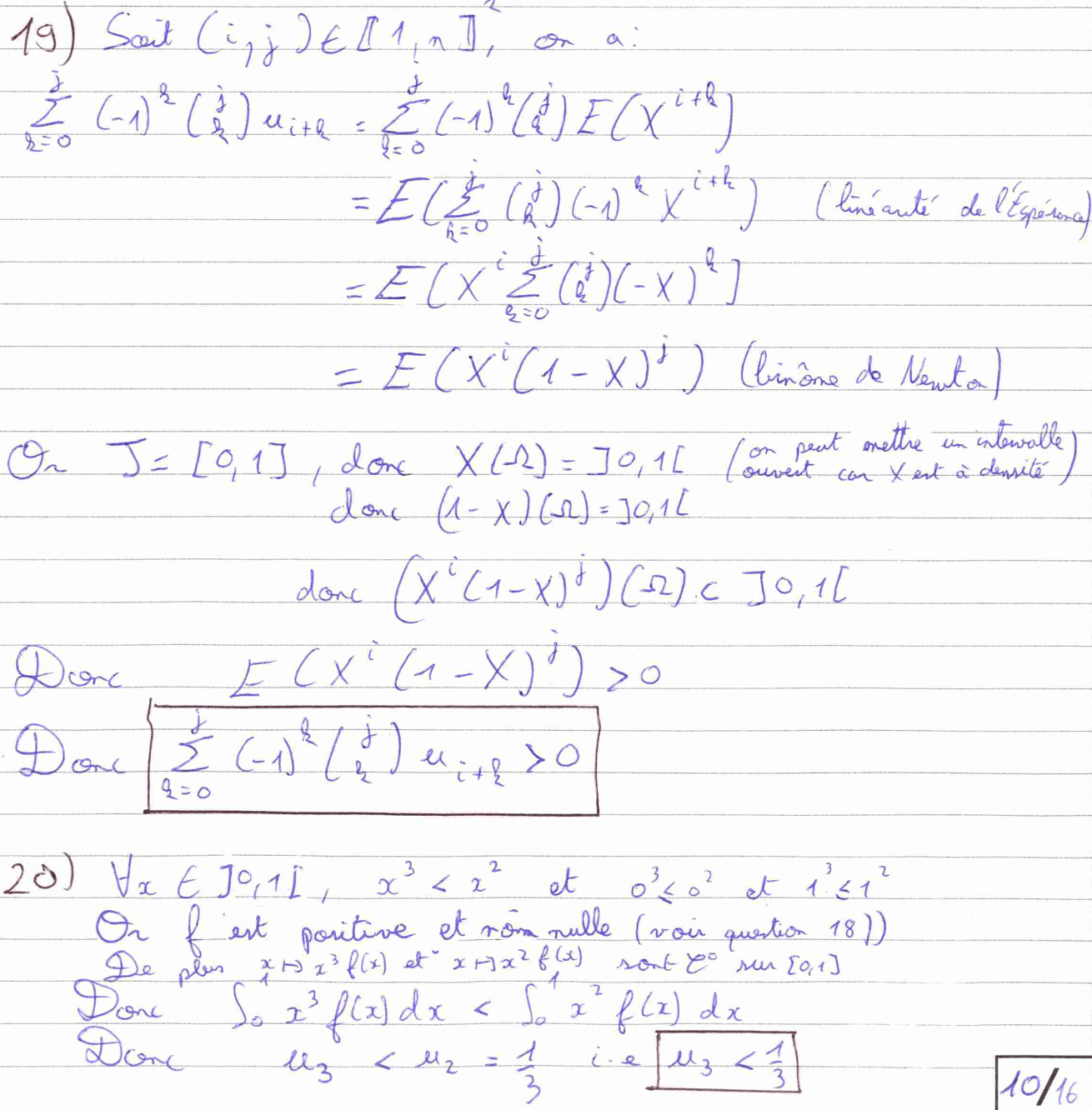
![]()
La question 21 nécessite d’être précis sur les justifications que nous indiquerons, car il faut montrer la convergence de séries. C’est donc ce que j’ai essayé de faire en introduisant des variables qui jouent le rôle de minimum et maximum et en justifiant leur existence.

La première sous-partie de la partie III vient de s’achever et nous commençons cette nouvelle partie avec une question triviale qui vérifie simplement que nous avons compris la définition de l’objet introduit.
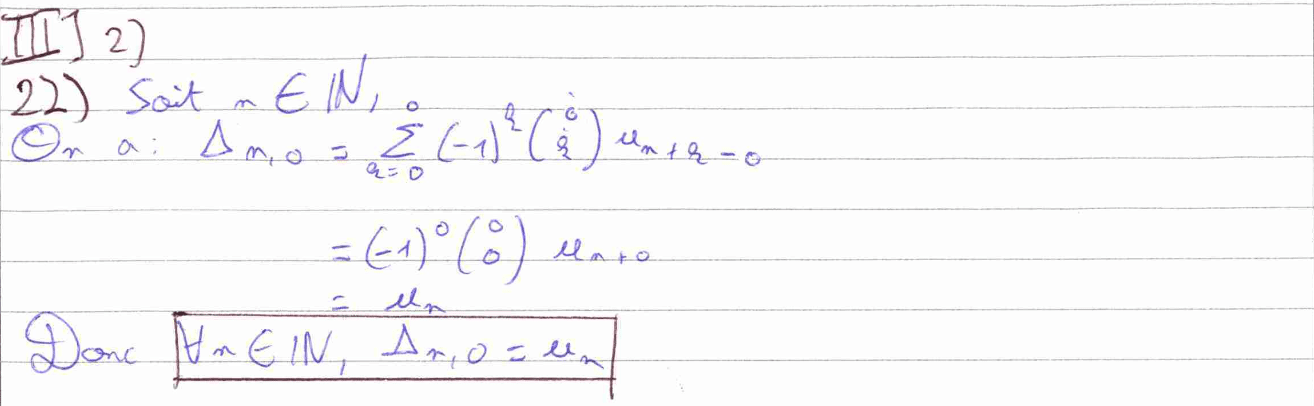
La question 23 est très similaire à la démonstration du binôme de Newton, il faut donc adopter un raisonnement similaire tout en indiquant l’utilisation d’un changement de variable.
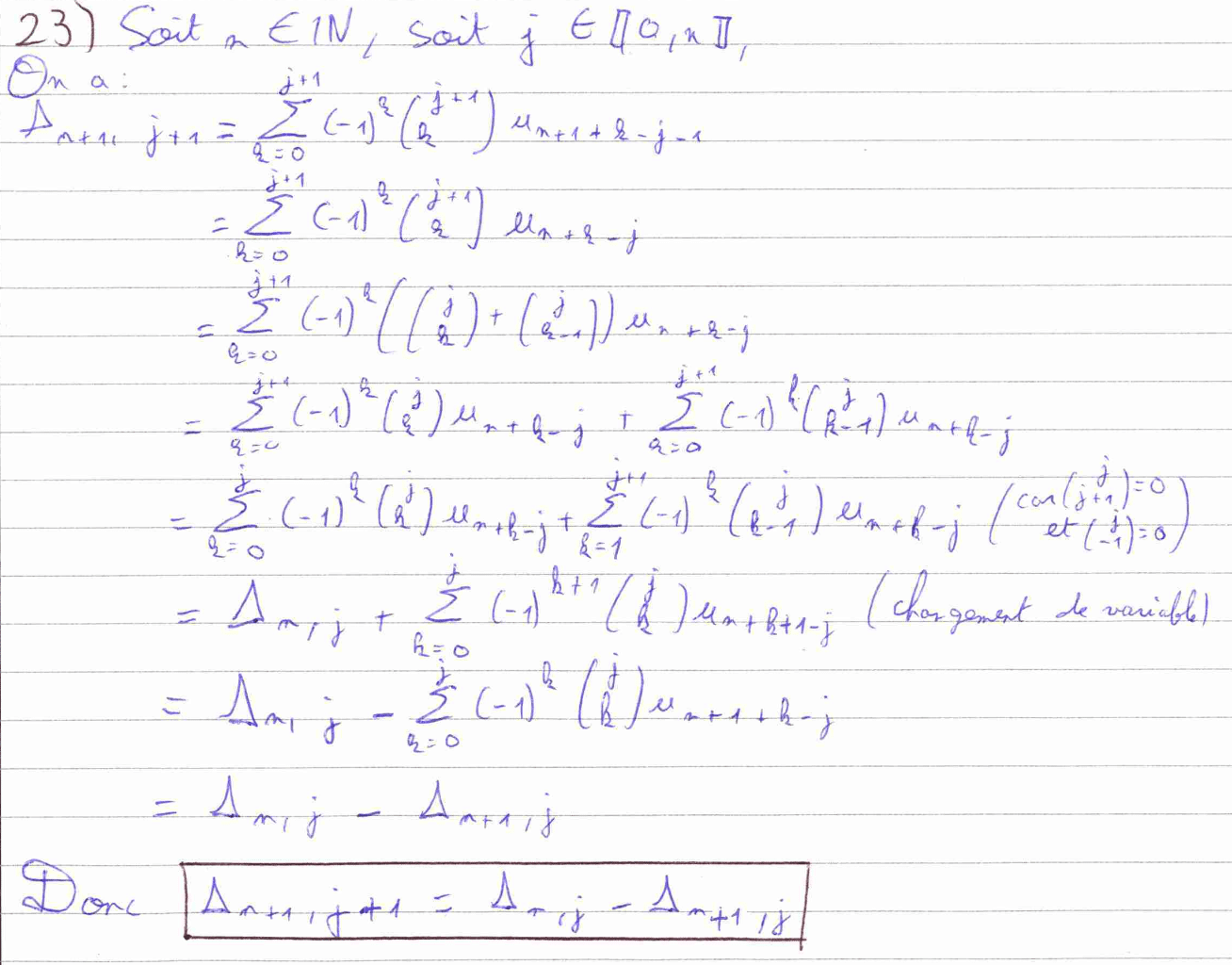
Les questions 24 et 25 sont deux questions de Python, la première était abordable et la seconde était plus complexe. J’ai pris l’initiative de recopier l’entièreté du script pour faciliter la lecture. Dans la question 24, j’ai fait une erreur à la sixième ligne « \(k\) in range(0, N+1) » et à la onzième ligne « Delta[k,j]=Delta[k-1,j-1]-Delta[k,j-1] ».

Nous passons maintenant à la troisième sous-partie de cette partie III. La question 26 nécessite d’être précis quant aux hypothèses annoncées. La rédaction d’une inégalité des accroissements finis doit être minutieusement rédigée d’où toutes mes remarques sur la continuité des fonctions et l’usage du théorème des bornes atteintes.


La question 27 demandait une fois de plus d’être rigoureux dans les calculs et de faire attention à quelques points de rédaction. Pour la 27a, il ne fallait pas confondre \(X \; \text{et} \; X(\omega)\), une erreur classique. Il fallait aussi bien penser à utiliser la croissance de l’espérance, une propriété qui est rarement utilisée. Quant à la 27b, il fallait raisonner par équivalence et bien penser à dire que la dernière assertion de l’équivalence est vraie pour que le raisonnement soit cohérent.

À partir de la question 28, il me restait peu de temps pour finir et j’ai commencé à accélérer et à passer les questions qui n’étaient pas évidentes. Ainsi je n’ai fait que la moitié « facile » de la question 28 en utilisant la fameuse propriété « \( \forall x \in [0,1], x(1-x) \le \frac{1}{4} \) » et j’ai admis le résultat de la question 29.
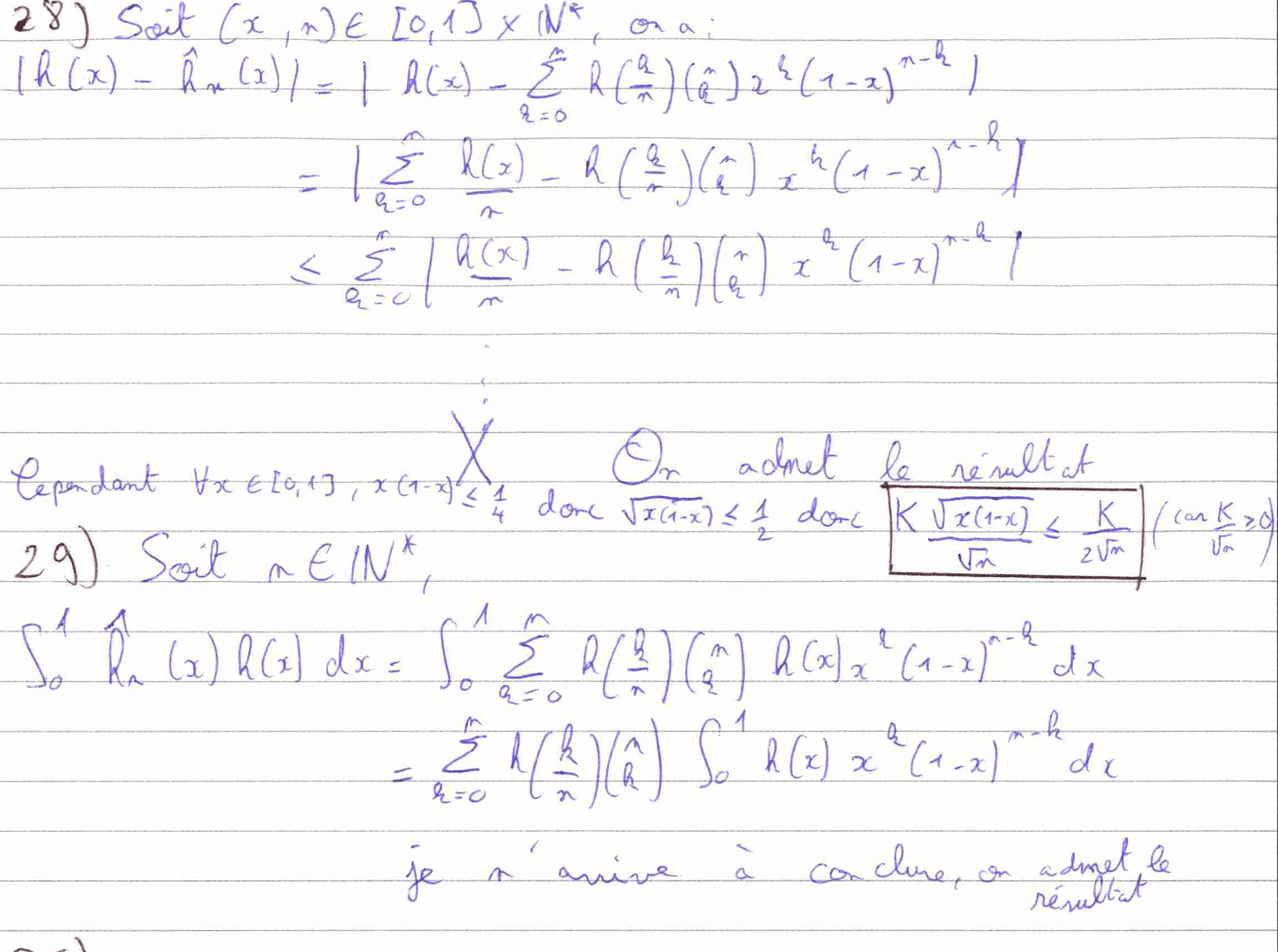
Les questions 30 et 31 ne nécessitaient pas des raisonnements très complexes, mais simplement l’utilisation des résultats précédemment démontrés ou admis. En effet, même si tu passes une question, tu peux et tu dois utiliser le résultat qu’elle t’offre. D’où l’intérêt de bien assimiler le résultat d’une question que tu as passée.
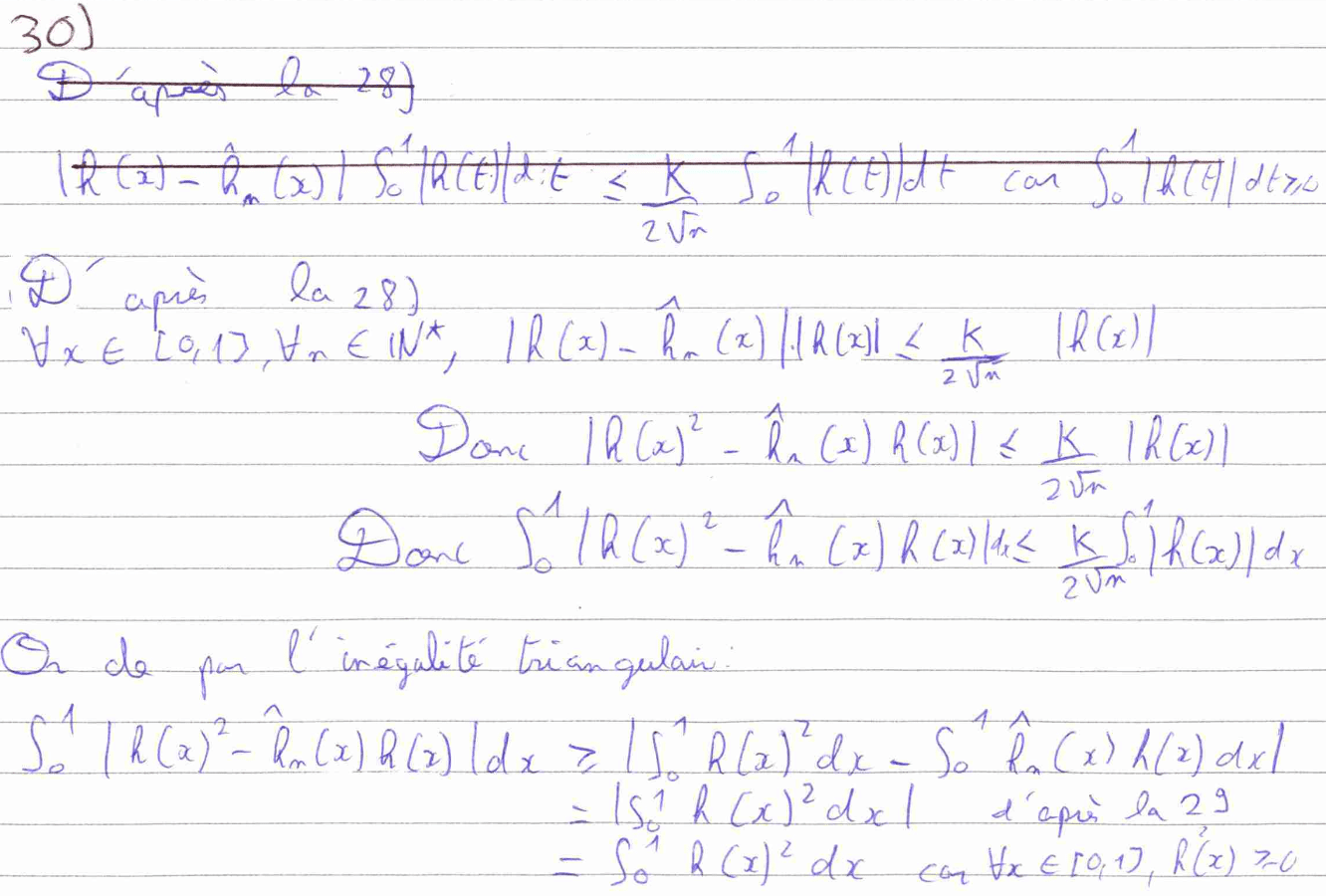

Une fin de sujet discriminante, mais non nécessaire
Nous arrivons enfin à la dernière sous-partie du sujet qui porte sur le problème de Hausdorff tronqué et qui nous fait manipuler des fonctions à plusieurs variables. Je n’ai pu finir que partiellement la première question. Cela montre une fois de plus qu’il n’est pas nécessaire de finir un sujet HEC pour avoir 20.

Conclusion
En somme, l’épreuve de mathématiques approfondies de HEC est connue pour sa complexité et son caractère redoutable. Cependant, j’espère que cette analyse approfondie de ma copie t’a montré que la réussite est à ta portée avec du dévouement, de la persévérance et des compétences bien ciblées.
De plus, la réussite en Maths I ne nécessite pas nécessairement de finir le sujet en entier. La clé réside dans la compréhension des concepts mathématiques présentés, la maîtrise du cours, la rigueur dans la rédaction et la persévérance face aux difficultés.
N’hésite pas à consulter toutes nos ressources mathématiques.













