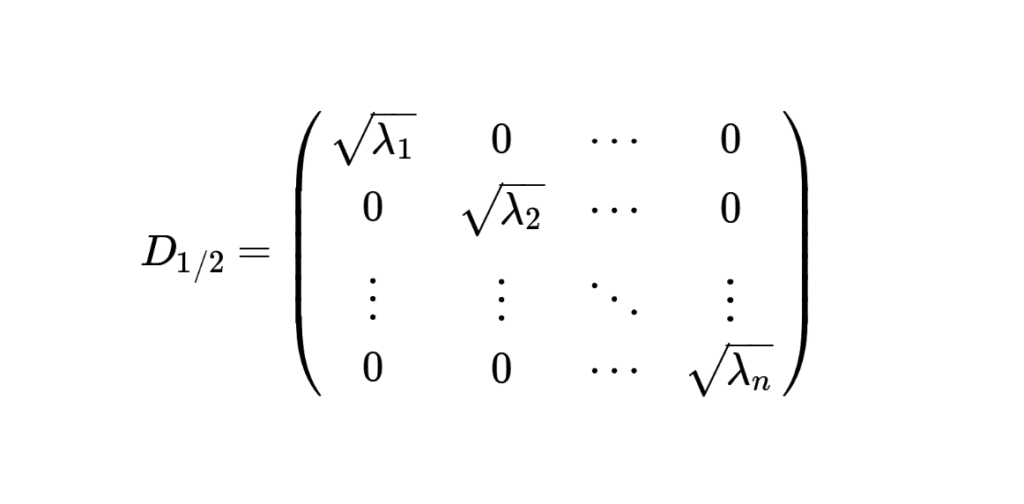Les matrices sont un outil fondamental en mathématiques, jouant un rôle crucial dans de nombreux domaines tels que l’algèbre linéaire, l’analyse numérique et même les statistiques. Leur compréhension approfondie permet non seulement de résoudre des problèmes complexes mais aussi de simplifier des calculs souvent considérés comme laborieux. Que ce soit pour le calcul des déterminants, la recherche des valeurs propres, ou la manipulation des inverses, les matrices recèlent de nombreuses astuces méconnues qui peuvent faire gagner un temps précieux et offrir des solutions élégantes. Dans cet article, nous allons explorer une série de techniques avancées mais accessibles, qui te permettront de maîtriser l’art de travailler avec les matrices.
1. Utiliser la trace pour déterminer une valeur propre manquante
La trace d’une matrice \( A \), notée \( \text{tr}(A) \), est la somme des éléments de sa diagonale principale. Elle est également égale à la somme de ses valeurs propres \( \lambda_i \). Cela peut être particulièrement utile si vous connaissez toutes les valeurs propres sauf une. Par exemple, si une matrice \( A \) de taille \( n \) a \( n-1 \) valeurs propres connues \( \lambda_1, \lambda_2, \ldots, \lambda_{n-1} \), la valeur propre manquante \( \lambda_n \) peut être déterminée en utilisant la formule suivante :
\[ \lambda_n = \text{tr}(A) – \sum_{i=1}^{n-1} \lambda_i \]
Supposons que nous ayons une matrice \( A \) avec une trace de 20 et les valeurs propres connues sont 3, 7, et 4. La valeur propre manquante serait alors :
\[ \lambda_4 = 20 – (3 + 7 + 4) = 6 \]
Cette méthode est particulièrement utile pour vérifier tes calculs de valeurs propres.
2. Calculer le déterminant d’une matrice triangulaire
Pour une matrice triangulaire de taille, qu’elle soit supérieure ou inférieure, le déterminant est simplement le produit des éléments de la diagonale principale. Cela simplifie grandement les calculs, surtout pour les grandes matrices. Si \( A \) est une matrice triangulaire de dimension \( n \times n \), alors :
\[ \det(A) = \prod_{i=1}^{n} a_{ii} \]
Prenons une matrice triangulaire supérieure \( A \) de dimension \( 2 \times 2 \) comme exemple :
\[ A = \begin{pmatrix}
2 & 3 \\
0 & 4
\end{pmatrix} \]
Le déterminant de \( A \) est alors :
\[ \det(A) = 2 \times 4 = 8 \]
De manière similaire, pour une matrice triangulaire inférieure \( B \) de dimension \( 2 \times 2 \) :
\[ B = \begin{pmatrix}
5 & 0 \\
7 & 6
\end{pmatrix} \]
Le déterminant de \( B \) est :
\[ \det(B) = 5 \times 6 = 30 \]
Cette propriété est extrêmement utile car elle permet de calculer rapidement le déterminant sans avoir à effectuer de longs calculs de cofacteurs. Pour des matrices plus grandes, cette astuce devient encore plus précieuse, économisant du temps et réduisant la complexité des calculs.
3. Utiliser les vecteurs propres pour la diagonalisation
Une matrice \( A \) est diagonalisable si et seulement si elle possède \( n \) vecteurs propres linéairement indépendants. Diagonaliser une matrice peut simplifier de nombreux calculs, notamment la puissance d’une matrice. Si \( P \) est la matrice formée par les vecteurs propres de \( A \) comme colonnes, alors :
\[ A = P D P^{-1} \]
où \( D \) est une matrice diagonale contenant les valeurs propres de \( A \). Par exemple, si \( A \) a pour vecteurs propres \( v_1, v_2 \), et \( v_3 \), et pour valeurs propres \( \lambda_1, \lambda_2 \), et \( \lambda_3 \), alors :
\[ P = \begin{pmatrix}
| & | & | \\
v_1 & v_2 & v_3 \\
| & | & |
\end{pmatrix} \]
et
\[ D = \begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_2 & 0 \\
0 & 0 & \lambda_3
\end{pmatrix} \]
4. Propriétés de la matrice inverse
Une propriété importante des matrices inversibles est que l’inverse de la transposée est la transposée de l’inverse. Autrement dit, si \( A \) est une matrice inversible, alors :
\[ (A^{-1})^T = (A^T)^{-1} \]
De plus, pour une matrice diagonale \( D \), son inverse est simplement une matrice diagonale avec les inverses des éléments diagonaux de \( D \). Par exemple, si :
\[ D = \begin{pmatrix}
d_1 & 0 & 0 \\
0 & d_2 & 0 \\
0 & 0 & d_3
\end{pmatrix} \]
alors
\[ D^{-1} = \begin{pmatrix}
\frac{1}{d_1} & 0 & 0 \\
0 & \frac{1}{d_2} & 0 \\
0 & 0 & \frac{1}{d_3}
\end{pmatrix} \]
Ces propriétés simplifient considérablement les calculs impliquant des matrices inversibles et diagonales.
5. La puissance d’une matrice diagonale
Lorsqu’une matrice est diagonale, élever cette matrice à une puissance quelconque devient particulièrement simple. Pour une matrice diagonale \( D \) de dimension \( n \times n \) :
\[ D = \begin{pmatrix}
d_1 & 0 & \cdots & 0 \\
0 & d_2 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n
\end{pmatrix} \]
Pour élever \( D \) à la puissance \( k \), il suffit d’élever chaque élément diagonal à cette puissance :
\[ D^k = \begin{pmatrix}
d_1^k & 0 & \cdots & 0 \\
0 & d_2^k & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & d_n^k
\end{pmatrix} \]
Par exemple, considérons une matrice diagonale \( D \) de dimension \( 2 \times 2 \) :
\[ D = \begin{pmatrix}
3 & 0 \\
0 & 4
\end{pmatrix} \]
Pour calculer \( D^3 \), nous élevons simplement chaque élément diagonal à la puissance 3 :
\[ D^3 = \begin{pmatrix}
3^3 & 0 \\
0 & 4^3
\end{pmatrix} = \begin{pmatrix}
27 & 0 \\
0 & 64
\end{pmatrix} \]
Cette méthode permet de simplifier considérablement les calculs, surtout pour les matrices de grandes dimensions.
6. La puissance d’une matrice diagonalisable
Si une matrice \( A \) est diagonalisable, il devient beaucoup plus simple de calculer ses puissances. Si \( A = P D P^{-1} \), où \( D \) est une matrice diagonale contenant les valeurs propres de \( A \), alors pour tout entier positif \( k \), on a :
\[ A^k = P D^k P^{-1} \]
Calculer \( D^k \) est facile puisque \( D \) est diagonale ; il suffit d’élever chaque valeur propre à la puissance \( k \). Par exemple, si :
\[ D = \begin{pmatrix}
\lambda_1 & 0 & 0 \\
0 & \lambda_2 & 0 \\
0 & 0 & \lambda_3
\end{pmatrix} \]
alors
\[ D^k = \begin{pmatrix}
\lambda_1^k & 0 & 0 \\
0 & \lambda_2^k & 0 \\
0 & 0 & \lambda_3^k
\end{pmatrix} \]
Ainsi, \( A^k \) se calcule efficacement en utilisant cette méthode.
7. Utiliser les propriétés des matrices de projecteurs
Les matrices de projecteurs, aussi appelées matrices de projection, jouent un rôle important dans l’algèbre linéaire, notamment en analyse et en géométrie. Une matrice \( P \) est dite projecteur si \( P^2 = P \). Cela signifie que lorsque \( P \) est appliquée deux fois, le résultat est le même que lorsqu’elle est appliquée une seule fois. Voici quelques propriétés et astuces pour travailler avec les matrices de projecteurs.
Propriété 1 : Idempotence
Pour une matrice projecteur \( P \), la relation \( P^2 = P \) est toujours vraie. Cela peut être utilisé pour simplifier les calculs impliquant des puissances de \( P \). Par exemple, pour toute puissance \( n \) :
\[ P^n = P \]
Propriété 2 : Valeurs propres
Les valeurs propres d’une matrice projecteur \( P \) sont toujours \( 0 \) ou \( 1 \). Cela découle directement de la propriété idempotente. Si \( \lambda \) est une valeur propre de \( P \) avec \( v \) le vecteur propre associé, alors :
\[ P v = \lambda v \]
et en appliquant à nouveau \( P \) :
\[ P(P v) = P(\lambda v) = \lambda (P v) = \lambda (\lambda v) = \lambda^2 v \]
mais puisque \( P v = \lambda v \), il s’ensuit que \( \lambda^2 = \lambda \), donc \( \lambda (\lambda – 1) = 0 \). Ainsi, \( \lambda = 0 \) ou \( \lambda = 1 \).
Propriété 3 : Trace
La trace d’une matrice projecteur \( P \), notée \( \text{tr}(P) \), est égale au rang de \( P \), c’est-à-dire au nombre de ses valeurs propres égales à 1. Cela peut être utilisé pour déterminer le rang de la matrice facilement.
8. Matrices commutantes et diagonalisation simultanée
Si deux matrices \( A \) et \( B \) commutent, c’est-à-dire \( AB = BA \), et sont diagonalisables, alors elles sont simultanément diagonalisables. Cela signifie qu’il existe une matrice \( P \) telle que :
\[ A = P D_A P^{-1} \]
et
\[ B = P D_B P^{-1} \]
où \( D_A \) et \( D_B \) sont des matrices diagonales. Cette propriété est très utile dans l’étude des systèmes de matrices qui apparaissent dans des problèmes linéaires couplés. Par exemple, si \( A \) et \( B \) ont des vecteurs propres communs, il est possible de choisir une base de vecteurs propres qui diagonalise les deux matrices simultanément, simplifiant ainsi l’analyse de leurs propriétés.
9. Utiliser les racines carrées de matrices
La recherche des racines carrées de matrices est un concept avancé mais très utile dans plusieurs domaines des mathématiques, y compris la résolution d’équations différentielles et l’optimisation. Une matrice \( B \) est une racine carrée d’une matrice \( A \) si \( B^2 = A \). Voici comment trouver et utiliser les racines carrées de matrices, en particulier pour les matrices symétriques positives.
Si une matrice \( A \) est diagonalisable, c’est-à-dire qu’il existe une matrice inversible \( P \) et une matrice diagonale \( D \) telles que :
\[ A = P D P^{-1} \]
alors la racine carrée de \( A \) peut être trouvée en prenant la racine carrée de chaque élément de \( D \). Pour cela, les valeurs propres de \( A \) doivent être positives afin que leurs racines carrées soient bien définies. Si \( D \) est une matrice diagonale avec des valeurs propres \( \lambda_1, \lambda_2, \ldots, \lambda_n \) sur la diagonale, alors :
\[ D_{1/2} = \begin{pmatrix}
\sqrt{\lambda_1} & 0 & \cdots & 0 \\
0 & \sqrt{\lambda_2} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \sqrt{\lambda_n}
\end{pmatrix} \]
La racine carrée de \( A \) est alors : \( B = P D_{1/2} P^{-1} \) et \( B^2 = A \)
Conclusion
Les matrices, avec leur structure et leurs propriétés riches, constituent un domaine fascinant des mathématiques. Les astuces présentées dans cet article montrent qu’il existe souvent des méthodes efficaces pour aborder les calculs matriciels. Que ce soit pour déterminer une valeur propre manquante à l’aide de la trace, calculer rapidement le déterminant d’une matrice triangulaire, ou exploiter les propriétés de la diagonalisation, ces techniques peuvent grandement simplifier ton travail.
Pour t’entrainer à utiliser ces astuces, tu peux réaliser les sujets suivants :
- Maths I 2016 (mathématiques approfondies)
- Ecricome 2023 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !