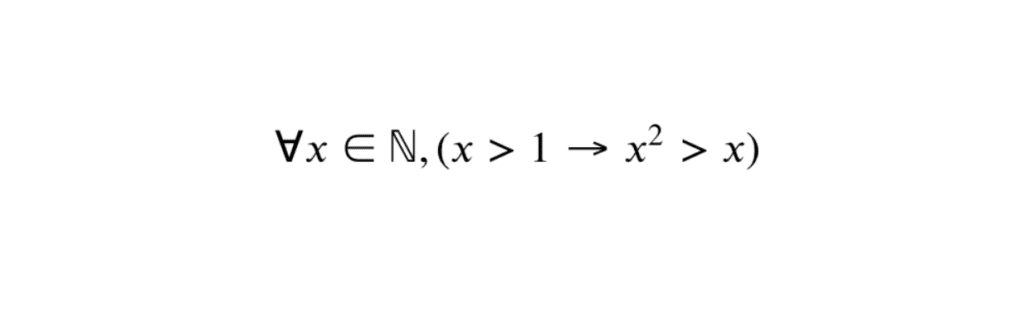Les quantificateurs jouent un rôle central en logique mathématique, permettant de formuler des propositions qui expriment des généralités ou des spécificités à propos des ensembles de nombres et d’autres objets mathématiques. Les deux principaux quantificateurs sont le quantificateur universel (\(\forall\)), qui se traduit par “pour tout”, et le quantificateur existentiel (\(\exists\)), qui signifie “il existe”. Comprendre comment et quand les utiliser est crucial pour la résolution de problèmes et la démonstration de théorèmes en mathématiques. Cet article vous propose plusieurs astuces pour maîtriser l’usage des quantificateurs à travers des exemples et explications clairs.
Astuce 1 : Utilisation stratégique de contre-exemples avec il existe
Le quantificateur existentiel peut induire en erreur, en particulier lorsqu’il s’agit de réfuter une proposition. Trouver un contre-exemple adéquat est souvent la méthode la plus directe et la plus convaincante pour démontrer l’invalidité d’une proposition utilisant \(\exists\).
Illustration approfondie avec un contre-exemple pour les quantificateurs
Pour contester la proposition \(\exists x \in \mathbb{R}, x^2 < 0\), il faut montrer que pour tout \(x\) réel, \(x^2\) est non négatif. Ce raisonnement est basé sur les propriétés fondamentales des nombres réels et leur carré. En démontrant l’impossibilité pour tout nombre réel de satisfaire \(x^2 < 0\), le contre-exemple invalide l’affirmation initiale de manière claire et concise.
Astuce 2 : Transformation des quantificateurs pour simplifier les arguments
La négation d’une proposition quantifiée transforme le type de quantificateur et modifie la condition associée, un principe utile pour réorganiser et simplifier les preuves.
Exemple de transformation en profondeur pour les quantificateurs
Considérons \(\forall x \in \mathbb{N}, x^2 \geq x\). Sa négation, \(\exists x \in \mathbb{N}, x^2 < x\), illustre comment la transformation d’un quantificateur universel en existentiel permet d’orienter la recherche vers un exemple spécifique qui réfute la généralité de la proposition originale. Cette technique est particulièrement puissante dans les preuves par l’absurde où identifier un tel exemple peut directement invalider une supposition universelle.
Astuce 3 : Quantificateurs et récurrence – Éviter les formulations erronées
Dans les preuves par récurrence, il est crucial de bien formuler l’hypothèse de récurrence pour éviter des erreurs de logique. Un écueil fréquent chez les étudiants est d’intégrer inappropriément le quantificateur universel (\(\forall\)) dans l’énoncé de la proposition de récurrence.
Erreur courante dans la formulation de la récurrence
Un exemple typique de cette erreur est la rédaction suivante pour une preuve que chaque terme d’une suite est supérieur au précédent (\(u_{n+1} > u_n\)) : “Montrons par récurrence sur l’entier naturel \(n\) que \(P(n)\) : \(\forall n, u_{n+1} > u_n\).” Cette formulation est incorrecte car elle suggère que la propriété est vraie pour tous les entiers naturels simultanément dès le début de la preuve, ce qui neutralise l’essence même de l’approche par récurrence qui est de construire la vérité de la proposition pas à pas, de \(n\) à \(n+1\).
Formulation correcte de la proposition de récurrence
La manière appropriée de formuler la récurrence dans ce contexte est de spécifier clairement que l’hypothèse de récurrence concerne un seul terme à la fois. Par exemple, la proposition de récurrence devrait être écrite comme suit : “Supposons que \(P(n)\) soit vrai, c’est-à-dire que \(u_n > u_{n-1}\). Nous devons alors démontrer que \(P(n+1)\) est également vraie, soit \(u_{n+1} > u_n\).” Cette rédaction évite l’usage du quantificateur universel et confirme que l’objectif est de prouver la relation entre les termes consécutifs de manière séquentielle.
En résumant, il est vital pour les étudiants de reconnaître que l’usage du quantificateur universel dans l’énoncé de récurrence pour des suites ou des séquences peut introduire des erreurs conceptuelles. L’accent doit être mis sur l’établissement d’une connexion logique entre chaque terme consécutif, un par un, conformément aux principes de la récurrence.
Astuce 4 : Maîtrise de la portée des quantificateurs
La portée d’un quantificateur délimite son effet sur les variables et les propositions dans lesquelles il est engagé. Une mauvaise interprétation de cette portée peut conduire à des conclusions erronées ou à des malentendus dans le raisonnement mathématique. Pour assurer la clarté, il est crucial d’utiliser des parenthèses de manière appropriée et de spécifier explicitement les ensembles concernés par le quantificateur.
Approfondissement sur la spécification de la portée
Considérons la proposition suivante : \(\forall x \in \mathbb{N}, (x > 1 \rightarrow x^2 > x)\). Ici, le quantificateur universel (\(\forall\)) s’applique explicitement à tout \(x\) dans l’ensemble des nombres naturels (\(\mathbb{N}\)). L’expression entre parenthèses précise la condition sous laquelle la conclusion \(x^2 > x\) doit être évaluée. Cette structuration aide à éviter l’ambiguïté quant à l’application de la condition et à la validité de la conclusion.
Astuce 5 : Analyse de la dépendance entre quantificateurs
L’interaction entre plusieurs quantificateurs dans une expression mathématique nécessite une analyse précise pour comprendre la relation et la dépendance entre les variables impliquées.
Détail sur la hiérarchie et l’interaction des quantificateurs
Dans l’expression \(\forall x \; \exists y, x < y\), le quantificateur existentiel (\(\exists\)) est conditionné par chaque valeur de \(x\) déterminée par le quantificateur universel (\(\forall\)). Cette structure implique que pour chaque \(x\), indépendamment choisi, il doit exister un \(y\) qui satisfait la condition \(x < y\). Comprendre cette dépendance est crucial pour interpréter correctement l’ensemble de la proposition et pour structurer des preuves qui utilisent cette forme de quantification.
Astuce 6 : Utilisation des quantificateurs dans les preuves par contradiction
Les preuves par contradiction, intégrant des quantificateurs, offrent un moyen puissant de démontrer la véracité d’une proposition en commençant par supposer que sa négation est vraie et en démontrant que cette hypothèse mène à une contradiction.
Méthodologie détaillée pour une preuve par contradiction
Pour prouver \(\exists x \in \mathbb{N}, x + 5 = 10\), on peut supposer le contraire, soit \(\forall x \in \mathbb{N}, x + 5 \neq 10\). Cette supposition peut ensuite être analysée pour révéler une contradiction, telle que l’existence d’un \(x\) spécifique (dans ce cas, \(x = 5\)) qui satisfait la condition initiale, invalidant ainsi la supposition universelle et confirmant la proposition initiale par contradiction.
Conclusion
Les quantificateurs ne sont pas seulement des symboles; ils sont des composants essentiels des déclarations et des preuves en mathématiques. Une bonne maîtrise de leur utilisation peut grandement améliorer la capacité à raisonner et à résoudre des problèmes mathématiques complexes. En intégrant les astuces présentées, tu pourras améliorer ta rédaction et résoudre des exercices avec davantage de rigueur.
Pour t’entrainer à manipuler les quantificateurs tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques !