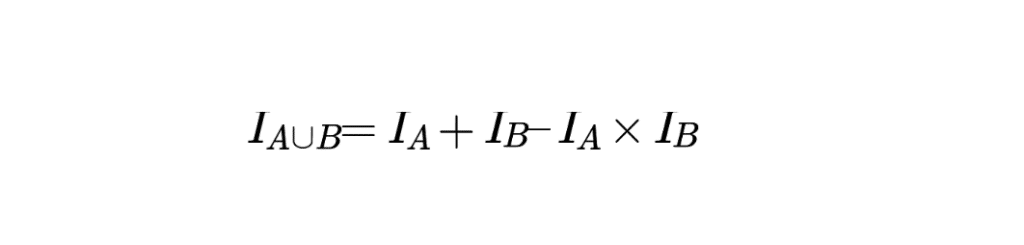Les variables indicatrices sont des outils puissants en mathématiques, notamment utilisées en probabilités et en statistiques. Une variable indicatrice prend la valeur 1 si un certain événement se produit et 0 dans le cas contraire. Elles simplifient souvent le calcul des probabilités et l’analyse des données en transformant des situations complexes en termes binaires faciles à manipuler. Cet article explore des astuces pour utiliser efficacement les variables indicatrices dans divers contextes mathématiques.
Astuce 1 : Définir clairement l’événement associé à la variable indicatrice
Pour exploiter pleinement le potentiel des variables indicatrices, il est crucial de définir avec précision l’événement qu’elles représentent. Cette définition claire est fondamentale car la moindre ambiguïté peut conduire à des erreurs dans le calcul des probabilités ou dans l’interprétation des résultats statistiques. Par exemple, dans une étude sur le comportement des consommateurs, une variable indicatrice pourrait être utilisée pour identifier les acheteurs de certains produits. Définir précisément ce qui qualifie un “acheteur” (ex : achat au moins une fois pendant la période d’étude) est essentiel pour garantir la fiabilité des analyses ultérieures.
Importance de la définition précise de la variable indicatrice
Supposez que tu travailles sur un problème impliquant des lancers de dés et que tu définis une variable indicatrice \( I \) telle que \( I = 1 \) si le résultat du lancer est un nombre pair. Il est essentiel de spécifier que \( I = 0 \) dans tous les autres cas (résultat impair), pour éviter toute confusion dans les calculs ultérieurs. Une définition imprécise peut rendre les analyses subséquentes non seulement incorrectes mais également trompeuses, affectant la qualité des décisions basées sur ces analyses.
Astuce 2 : Calcul de l’espérance d’une variable indicatrice
Les variables indicatrices ne simplifient pas seulement le calcul des fréquences et des probabilités, mais elles sont également très utiles pour déterminer l’espérance mathématique dans des contextes probabilistes. L’espérance d’une variable indicatrice est particulièrement simple à calculer et fournit des insights précieux dans l’analyse des phénomènes aléatoires.
Principe du calcul de l’espérance pour une variable indicatrice
L’espérance d’une variable indicatrice \( I_A \) correspondant à un événement \( A \) est égale à la probabilité que cet événement se produise. Autrement dit, si \( I_A = 1 \) lorsque \( A \) se produit et \( I_A = 0 \) autrement, alors l’espérance de \( I_A \), notée \( E(I_A) \), est simplement \( P(A) \).
\[ E(I_A) = 1 \cdot P(A) + 0 \cdot P(\neg A) = P(A) \]
Cette relation est directe car la définition même d’une variable indicatrice encode l’occurrence de l’événement \( A \) avec la valeur 1 et son absence avec la valeur 0. Ainsi, le calcul de l’espérance se réduit à la probabilité que l’événement \( A \) se produise.
Astuce 3 : Combinaison de variables indicatrices pour étudier des événements multiples
L’utilisation conjointe de plusieurs variables indicatrices permet d’examiner les interactions entre différents événements, ce qui est extrêmement bénéfique dans les études de probabilité et les analyses statistiques multivariées. Cette technique est particulièrement efficace pour étudier la cooccurrence d’événements et leurs interactions possibles.
Stratégie pour les événements multiples autour des variables indicatrices
Pour deux événements \( A \) et \( B \), définissez deux variables indicatrices \( I_A \) et \( I_B \). La variable \( I_{A \cap B} = I_A \times I_B \) représente alors l’indicateur de l’intersection des événements \( A \) et \( B \). Cette approche permet de simplifier l’analyse des probabilités conjointes et des interactions entre événements, offrant un moyen direct d’évaluer l’indépendance ou la dépendance entre \( A \) et \( B \) à travers l’analyse de leurs variables indicatrices respectives.
Astuce 4 : Utilisation des variables indicatrices pour l’union d’événements
Les variables indicatrices peuvent également être utilisées efficacement pour analyser l’union de deux événements ou plus. Cette approche permet d’exploiter les propriétés algébriques des variables indicatrices pour simplifier le calcul des probabilités de l’union d’événements.
Formule de la variable indicatrice pour l’union
Pour deux événements \( A \) et \( B \), la variable indicatrice pour l’union de \( A \) et \( B \) (\( A \cup B \)) peut être exprimée à l’aide des variables indicatrices \( I_A \) et \( I_B \) de \( A \) et \( B \) respectivement. La variable indicatrice pour \( A \cup B \), notée \( I_{A \cup B} \), est définie par :
\[ I_{A \cup B} = \max(I_A, I_B) \]
ou, de manière équivalente, par l’expression :
\[ I_{A \cup B} = I_A + I_B – I_A \times I_B \]
Cette dernière formule est particulièrement utile car elle reflète directement la formule d’inclusion-exclusion pour les probabilités, permettant de calculer \( P(A \cup B) \) comme suit :
\[ P(A \cup B) = P(A) + P(B) – P(A \cap B) \]
En termes de variables indicatrices, cela se traduit par :
\[ E(I_{A \cup B}) = E(I_A) + E(I_B) – E(I_A \times I_B) \]
où \( E(I_{A \cup B}) \) représente l’espérance de la variable indicatrice pour l’union des événements \( A \) et \( B \).
Cette technique est particulièrement utile pour simplifier les calculs dans les études où plusieurs événements se chevauchent, permettant une analyse plus fine et rapide des probabilités étudiées.
Astuce 5 : Utiliser les variables indicatrices pour simplifier les sommes
Les variables indicatrices peuvent transformer des opérations complexes en expressions plus simples, particulièrement utiles lors du comptage du nombre d’occurrences d’un événement. Cette simplification est particulièrement avantageuse dans le calcul de fréquences ou de probabilités. Par exemple, dans le contexte d’une enquête de satisfaction, une variable indicatrice peut être définie pour chaque répondant exprimant une satisfaction (valeur 1) ou non (valeur 0). La moyenne de ces variables indicatrices donne directement la proportion des répondants satisfaits.
Exemple d’application
Si vous souhaitez calculer le nombre de jours pluvieux sur une période de 30 jours, vous pouvez définir une variable indicatrice \( I_i \) pour chaque jour \( i \), où \( I_i = 1 \) si le jour est pluvieux, et \( I_i = 0 \) sinon. Le nombre total de jours pluvieux est alors simplement la somme des \( I_i \), soit \( \displaystyle \sum_{i=1}^{30} I_i \). Cette méthode élimine le besoin de parcourir manuellement les données pour compter les jours pluvieux, facilitant ainsi les analyses statistiques et les rapports.
Astuce 6 : Estimer les probabilités à l’aide des variables indicatrices
Les variables indicatrices sont extrêmement utiles pour estimer les probabilités d’événements complexes en les ramenant à des calculs de moyennes simples. Cette méthode est souvent employée dans les simulations Monte Carlo, où les variables indicatrices peuvent être utilisées pour modéliser une variété d’événements aléatoires et pour calculer des probabilités empiriques.
Méthode d’estimation
La probabilité d’un événement \( A \) peut être estimée par la moyenne des valeurs prises par la variable indicatrice associée, calculée sur de nombreuses répétitions de l’expérience. Si \( I_A \) est la variable indicatrice de \( A \) et que l’expérience est répétée \( n \) fois, alors \( P(A) \approx \frac{1}{n} \displaystyle \sum_{i=1}^n I_{A_i} \), où chaque \( I_{A_i} \) est évaluée lors de la \( i \)-ème répétition. Cette approche permet d’obtenir des estimations de probabilité précises même pour des événements rares ou complexes.
Conclusion
Les variables indicatrices offrent une méthode élégante et efficace pour gérer des données binaires et calculer des probabilités en mathématiques. En suivant les astuces présentées, tu pourras non seulement simplifier tes calculs mais aussi améliorer ta compréhension des événements étudiés. En effet, utiliser ces outils de manière judicieuse permet d’optimiser l’analyse des données et de renforcer la précision des études probabilistes et statistiques.
Pour t’entrainer sur les variables indicatrices tu peux réaliser ces sujets mathématiques approfondies :
Tu peux retrouver le méga répertoire qui contient toutes les annales de concours et leur corrigé ! Tu peux également accéder à toutes nos autres ressources mathématiques !