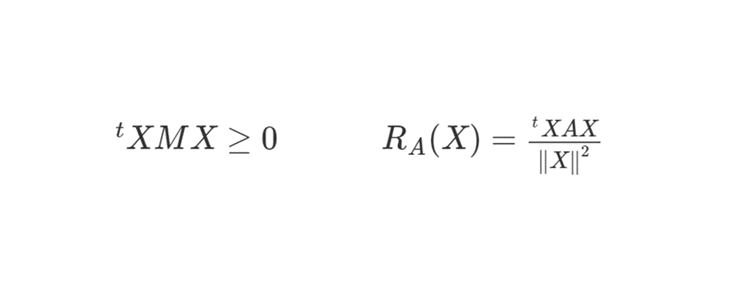
L’objectif de cet article est d’étudier des notions « classiques » qui tombent régulièrement dans les sujets et qui sont à la limite du programme. Tu trouveras ici de quoi mieux te faire comprendre la notion de matrices symétriques (définies) positives, ainsi que des liens vers des annales pour approfondir la notion. De même, l’article introduit le fameux quotient de Rayleigh, aux propriétés bien particulières !
Cet article peut être utile pour s’entraîner aux épreuves de l’EM et de l’EDHEC, mais aussi pour les Parisiennes. C’est pourquoi il est important d’être familier avec la notion pour la repérer facilement et gagner du temps et des points !
Attention, cet article est un article spécial maths approfondies. La théorie de l’algèbre bilinéaire n’est pas au programme des maths appliquées.
Les matrices symétriques (définies) positives
Définition
Une matrice symétrique \(M\in\mathcal{M}_{n}(\mathbb{R})\) est dite symétrique positive si pour tout \(X \in
\mathcal{M}_{n,1}(\mathbb{R})\), on a \({}^tXMX\geq 0\). On note \(M\in\mathcal{S}_{n}^{+}(\mathbb{R})\).
Une matrice symétrique \(M\in\mathcal{M}_{n}(\mathbb{R})\) est dite symétrique définie positive si pour tout \(X \in\mathcal{M}_{n,1}(\mathbb{R})\) avec \(X \ne 0\), on a \({}^tXMX> 0\). On note \(M\in\mathcal{S}_{n}^{+*}(\mathbb{R})\).
Remarque
\(M\) de \(\mathcal{M}_{n}(\mathbb{R})\) est symétrique positive (respectivement définie positive) \(\Leftrightarrow\) le spectre de \(M\) est inclus dans \(\mathbb{R}^{+}\) (respectivement \(\mathbb{R}_{*}^{+}\)).
Démonstration
Cette notion étant hors programme, il est important que tu saches refaire cette démonstration afin de gagner du temps en épreuve.
– On suppose \(M\in\mathcal{S}_{n}^{+*}(\mathbb{R})\).
Soit \(\lambda\) une valeur propre de \(M\), \(\exists X \ne 0\) tel que \(MX=\lambda X\)
Comme \(M\in\mathcal{S}_{n}^{+*}(\mathbb{R})\), alors \({}^tXMX\geq 0\).
Donc \(\underbrace{{}^tXMX}_{>0}= \lambda {}^tXX=\lambda \underbrace{\|X\|^2}_{>0} \). On a bien \(\lambda\in\mathbb{R}_{*}^{+}\).
– On suppose maintenant que les valeurs propres de \(M\) sont incluses dans \(\mathbb{R}_{*}^{+}\).
On sait que \(M\) est une matrice symétrique de \(\mathcal{M}_{n}(\mathbb{R})\), donc d’après le théorème spectral, il existe une matrice \(P\) orthogonale et une matrice \(D\) diagonale, dont les coefficients diagonaux sont les valeurs propres de \(M\). On note \( D=diag(\mu_1, \dots, \mu_n)\), où les \(\mu_i\) sont les \(\lambda_i\), mais potentiellement comptés plusieurs fois, en fonction de la dimension du sous-espace propre associé à la valeur propre \(\lambda_i\), telles que \(M={}^tPDP\).
Soit \(X \in\mathcal{M}_{n,1}(\mathbb{R})\), on a : \({}^tXMX={}^tX{}^tPDPX={}^t(PX)D(PX)\)
On peut alors noter : \({}^t (PX) D(PX)=\displaystyle \sum_{i=1}^{n}\mu_iy_i^2\). Donc \(\exists X \ne 0\), \(M\in\mathcal{S}_{n}^{+*}(\mathbb{R})\).
On retrouve ainsi l’équivalence.
Remarque
Si \(A\) et \(B\) sont symétriques définies positives, alors \(A+B\) l’est aussi.
Exemples
\(A=\begin{pmatrix} 3 & 0 \\ 0
& 8\end{pmatrix}\) est une matrice symétrique dont les valeurs propres sont 3 et 8, son spectre est donc inclus dans \(\mathbb{R}_{*}^{+}\). \(A\) est donc une matrice définie positive.
\(B=\begin{pmatrix} 1 & 1&1 \\ 1
& 1 &1 \\1 & 1 &1\end{pmatrix}\) est une matrice symétrique dont les valeurs propres sont 0 et 3, son spectre est donc inclus dans \(\mathbb{R}^{+}\). B est donc une matrice positive.
\(C=\begin{pmatrix} 6 & 3 \\ 3
& 6\end{pmatrix}\) est une matrice symétrique dont les valeurs propres sont 3 et 9, son spectre est donc inclus dans \(\mathbb{R}_{*}^{+}\). C’est donc une matrice définie positive.
\(D=A+C= \begin{pmatrix} 9 & 3 \\ 3
& 14\end{pmatrix}\) est la somme de deux matrices symétriques définies positives, D l’est donc aussi.
Application à l’optimisation
Maîtriser la notion de matrices symétriques définies positives et connaître la démonstration de l’équivalence avec le signe des valeurs propres peut être très utile dans le cadre de l’étude des hessiennes de fonctions à plusieurs variables, afin de montrer qu’un point critique est un minimum ou un maximum.
Soit \(f\) une fonction de \(\mathbb{R}^{n}\) dans \(\mathbb{R}\). Soit \(a\) un point critique de \(f\).
- Si \(\nabla^{2}(f)(a)\) (la matrice hessienne en \(a\)) est définie positive, alors \(a\) est un minimum au moins local de \(f\).
- Si \(\nabla^{2}(f)(a)\) est positive ( 0 est une valeur propre de la hessienne), alors \(a\) est un point col (ou point-selle) de \(f\).
Le quotient de Rayleigh
Le quotient de Rayleigh d’une matrice symétrique \(A\) est la fonction définie sur \(\mathbb{R}^{n}\) par : \(\forall x \in \mathbb R^n, R_A(x)=\frac{{}^txAx}{\|x\|^2}\).
La particularité de cette fonction est que ses points critiques sont les vecteurs propres de \(A\), et que la valeur prise par \(R_A\) en un vecteur propre vaut la valeur propre associée. L’étude de \(R_A\) permet de démontrer le célèbre encadrement de Rayleigh. Tu trouveras ici un article qui t’explique tous ses secrets.
L’exercice 1 du sujet d’Ecricome ECS 2005 (sujet, corrigé) te fait analyser un quotient de Rayleigh afin de retrouver ce résultat.
Pour approfondir
Tu peux t’entraîner sur les parties III et IV du problème 1 du sujet EML 2012 ECS (sujet et corrigé) et sur le problème 2 du sujet EML 2009 ECS (sujet et corrigé).
N’hésite pas à consulter toutes nos autres ressources de maths !
