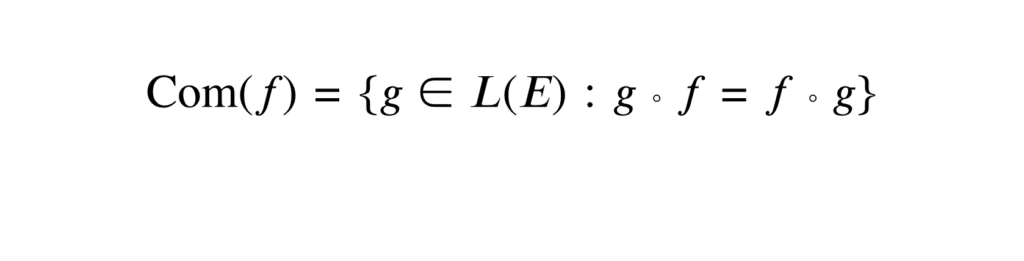L’algèbre linéaire est une branche essentielle des mathématiques qui explore les vecteurs, les espaces vectoriels, et les transformations linéaires, parmi lesquels les endomorphismes jouent un rôle central. Ces transformations, qui opèrent au sein d’un même espace vectoriel, sont cruciales pour analyser et comprendre les dynamiques internes de ces espaces. En particulier, l’étude des interactions entre endomorphismes à travers leur commutant, ou centralisateur, est vitale pour déchiffrer les propriétés structurelles et résoudre des problèmes complexes. Cet article détaille le concept du commutant d’un endomorphisme, ainsi que plusieurs de ses propriétés. Bien que cette notion soit hors programme, tu pourras être amené à la rencontrer aux épreuves parisiennes et aux oraux de mathématiques !
Qu’est-ce que le Commutant d’un Endomorphisme ?
Le commutant d’un endomorphisme, souvent désigné sous le terme de centralisateur, est l’ensemble des endomorphismes qui commutent avec cet endomorphisme donné. Pour un endomorphisme \( f \) d’un espace vectoriel \( E \), le commutant de \( f \), noté \( \text{Com}(f) \), est défini par :
\[ \text{Com}(f) = \{ g \in L(E) : g \circ f = f \circ g \} \]
où \( L(E) \) désigne l’ensemble de tous les endomorphismes de \( E \).
Le Lien entre Commutants de Matrices et d’Endomorphismes
Tout comme pour les endomorphismes, le commutant d’une matrice \( A \) comprend toutes les matrices \( B \) qui commutent avec \( A \), c’est-à-dire pour lesquelles \( AB = BA \). Cette relation de commutation est directement analogue à celle observée avec les endomorphismes, où deux opérations sont dites commuter si l’application de l’une suivie de l’autre produit le même résultat que leur application dans l’ordre inverse.
Les Propriétés Fondamentales
Le commutant d’un endomorphisme \( f \), noté \( \text{Com}(f) \), possède des propriétés algébriques et structurelles qui en font un sujet d’étude important en algèbre linéaire. Voici une liste organisée de ces propriétés :
1. Sous-espace vectoriel : \( \text{Com}(f) \) est un sous-espace vectoriel de l’ensemble \( L(E) \) des endomorphismes de l’espace vectoriel \( E \). Cela signifie que si \( g \) et \( h \) sont des endomorphismes qui commutent avec \( f \), alors toute combinaison linéaire de \( g \) et \( h \) commute également avec \( f \).
2. Stabilité sous composition : \( \text{Com}(f) \) est stable sous la composition des endomorphismes. Pour tous \( g, h \in \text{Com}(f) \), les compositions \( g \circ h \) et \( h \circ g \) sont aussi des membres de \( \text{Com}(f) \).
3. Stabilité de l’image et du noyau : Soient \(E\) un \( \mathbb{R} \text{-espace vectoriel}, \) \(f\) et \(g\) deux endomorphismes de \(E\) vérifiant \( g \circ f = f \circ g. \) Alors \( \text{Ker}(f) \; \text{et} \; \text{Im}(f) \) sont stables par \(g.\)
4. Fermeture par conjugaison : Si \( g \) appartient à \( \text{Com}(f) \) et \( h \) est un endomorphisme quelconque de \( E \), alors l’endomorphisme \( hgh^{-1} \) appartient également à \( \text{Com}(f) \), à condition que \( h \) commute avec \( f \). Cette propriété montre que \( \text{Com}(f) \) est invariant sous l’action de conjugaison par des endomorphismes qui commutent avec \( f \).
Ces propriétés rendent le commutant d’un endomorphisme non seulement intéressant du point de vue théorique mais également utile pour analyser des problèmes spécifiques où la commutativité des transformations joue un rôle crucial.
Exemples Concrets
Pour mieux comprendre le concept de commutation entre endomorphismes, considérons un espace vectoriel \( E \) et un endomorphisme \( f \) représenté par la matrice suivante dans une base choisie : \( \displaystyle F = \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} \)
Nous allons maintenant déterminer les conditions sous lesquelles un autre endomorphisme \( g \), représenté par une matrice générique \( \displaystyle G = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \), commute avec \( f \).
Pour que \( g \) et \( f \) commutent, les produits \( FG \) et \( GF \) doivent être égaux :
\[ FG = \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} a & b \\ 2c & 2d \end{pmatrix} \]
\[ GF = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix} = \begin{pmatrix} a & 2b \\ c & 2d \end{pmatrix} \]
Pour que ces deux produits soient égaux, nous devons avoir :
1. \( a = a \) (ce qui est toujours vrai),
2. \( b = 2b \) (ce qui implique \( b = 0 \)),
3. \( 2c = c \) (ce qui implique \( c = 0 \)),
4. \( 2d = 2d \) (ce qui est toujours vrai).
Le système d’équations \( b = 0 \) et \( c = 0 \) nous montre que pour que \( G \) commute avec \( F \), la matrice \( G \) doit avoir la forme :
\[ G = \begin{pmatrix} a & 0 \\ 0 & d \end{pmatrix} \]
Cela signifie que \( G \) peut être n’importe quelle matrice diagonale avec les entrées \( a \) et \( d \) sur la diagonale. Ces résultats indiquent que le commutant de \( f \), \( \text{Com}(f) \), est constitué de toutes les matrices diagonales dans cette base. Cette analyse illustre comment la structure spécifique de \( f \) détermine les propriétés et les contraintes des endomorphismes qui peuvent commuter avec lui.
Une condition nécessaire et suffisante pour que deux endomorphismes commutent
Pour deux endomorphismes \( f \) et \( g \) d’un espace vectoriel \( E \) de dimension finie sur \( \mathbb{R} \), où \( f \) est diagonalisable, une condition nécessaire et suffisante pour qu’ils commutent est que les sous-espaces propres de \( f \) soient stables par \( g \). Cette propriété se démontre en deux étapes claires.
Tout d’abord, si \( f \) et \( g \) commutent, alors pour tout polynôme \( P \), le noyau de \( P(f) \) est stable par \( g \). En particulier, pour \( P(X) = X – \lambda \) où \( \lambda \) est une valeur propre de \( f \), chaque sous-espace propre de \( f \) correspondant à \( \lambda \) est préservé par \( g \).
Réciproquement, si chaque sous-espace propre de \( f \) est stable par \( g \), alors pour tout vecteur propre \( x \) de \( f \) associé à \( \lambda \), l’application de \( g \) suivie de \( f \) est équivalente à l’application de \( f \) suivie de \( g \), c’est-à-dire \( g(f(x)) = g(\lambda x) = \lambda g(x) \) et \( f(g(x)) = \lambda g(x) \). Étant donné que \( f \) est diagonalisable, \( E \) se décompose en une somme directe des sous-espaces propres de \( f \), permettant de généraliser cette relation à tout \( E \) et ainsi démontrer que \( f(g(x)) = g(f(x)) \) pour tout \( x \) dans \( E \). Cette relation démontre donc que \( g \) et \( f \) commutent.
Conclusion
Le commutant d’un endomorphisme est plus qu’une simple collection d’endomorphismes; il représente un outil puissant pour analyser et comprendre les structures internes et les symétries dans différents contextes mathématiques. Pour les étudiants préparant les épreuves parisiennes et les oraux de mathématiques, maîtriser ce concept vous permet d’enrichir votre préparation et vos outils en algèbre linéaire.
Pour t’entrainer sur la notion de commutant d’endomorphisme tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques !