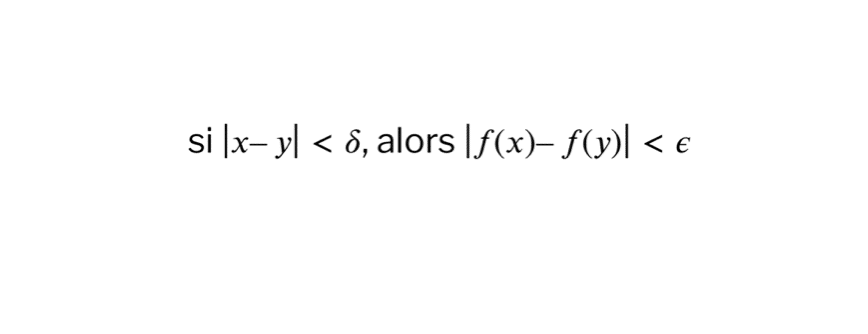La continuité uniforme est un concept fondamental en analyse mathématique, renforçant la notion de continuité d’une fonction. Ce concept est particulièrement utile en économie, où la stabilité et la prévisibilité des fonctions jouent un rôle crucial dans des modèles comme ceux de l’optimisation. Dans cet article, nous allons explorer la définition de la continuité uniforme, ses propriétés, et comment elle se distingue de la simple continuité. Nous illustrerons également le concept par des exemples pratiques pertinents pour les étudiants qui préparent les épreuves parisiennes !
Définition de la Continuité Uniforme
La continuité Point par Point
Pour qu’une fonction \( f: X \rightarrow Y \) soit continue en un point \( a \in X \), pour tout \( \epsilon > 0 \), il doit exister un \( \delta > 0 \) tel que pour tout \( x \in X \), si \( |x – a| < \delta \), alors \( |f(x) – f(a)| < \epsilon \). Cette définition dépend du point \( a \) et du choix de \( \delta \) qui peut varier d’un point à l’autre de \( X \).
La continuité uniforme
La continuité uniforme renforce cette idée en éliminant la dépendance au point \( a \). Une fonction \( f \) est dite uniformément continue sur \( X \) si, pour tout \( \epsilon > 0 \), il existe un \( \delta > 0 \) unique pour tout \( X \) tel que pour tous \( x, y \in X \), si \( |x – y| < \delta \), alors \( |f(x) – f(y)| < \epsilon \). Ici, \( \delta \) est constant pour tous les points de \( X \) et tous les écarts \( \epsilon \) choisis.
Remarque : Il est possible de reformuler cette définition pour l’étendre aux fonctions d’un espace vectoriel normé qui sont à valeurs dans un espace vectoriel normé. En effet, il suffit de remplacer toutes les valeurs absolues par des normes.
La continuité uniforme représente une condition plus rigoureuse que la continuité classique. D’un point de vue intuitif, une fonction qui n’est pas uniformément continue permet l’existence de paires de points extrêmement proches dont les images, cependant, ne sont pas aussi rapprochées. Par conséquent, des fonctions telles que \( \displaystyle f(x) = x^2 \) et \( \displaystyle g(x) = \sin(e^x) \) ne satisfont pas à la continuité uniforme sur l’ensemble des réels \( \mathbb{R} \).
Propriétés de la Continuité Uniforme
Le théorème de Heine
Si une fonction \( f: [a, b] \rightarrow \mathbb{R} \) est continue sur le segment fermé \([a, b]\), alors elle est aussi uniformément continue sur ce segment.
Ce résultat clé souligne que la variation d’une fonction sur un intervalle fermé et borné est non seulement contrôlée localement, mais de manière uniforme sur tout l’intervalle. Cela assure une prévisibilité et une stabilité importantes de la fonction sur toute la longueur du segment.
Les fonctions lipschitziennes
La notion de fonction lipschitzienne est essentielle en analyse mathématique pour étudier la stabilité et la régularité des fonctions. Une fonction \( f \) définie sur un intervalle \( I \) du réel \( \mathbb{R} \) est qualifiée de lipschitzienne si elle satisfait à la condition suivante : pour tout couple de points \( x, x’ \) dans \( I \), la différence entre les valeurs de \( f \) en ces points est majorée par \( k \) fois la distance entre \( x \) et \( x’ \), où \( k \) est une constante réelle positive. Mathématiquement, cela s’exprime comme \( |f(x) – f(x’)| \leq k|x – x’| \).
Remarque : Si la constante \( k \) est en plus inférieure à 1 (0 < \( k \) < 1), alors \( f \) est dite contractante, ce qui implique que \( f \) rapproche systématiquement les points.
Implications : Ces propriétés entraînent des implications directes en termes de continuité : une fonction lipschitzienne sur \( I \) est uniformément continue sur \( I \). De plus, toute fonction uniformément continue sur un intervalle est nécessairement continue sur cet intervalle. Il est important de noter, toutefois, que les réciproques de ces affirmations ne sont pas vraies, soulignant ainsi que les conditions de Lipschitz et de contraction imposent une régularité plus stricte que la simple continuité.
Exercices et Applications
Exercice 1
Soit la fonction \( f(x) = 3x + 7 \). Démontrer que \( f \) est uniformément continue sur \( \mathbb{R} \).
Nous devons montrer que pour tout \( \epsilon > 0 \), il existe un \( \delta > 0 \) tel que si \( |x – y| < \delta \), alors \( |f(x) – f(y)| < \epsilon \). Choisissons \( \displaystyle \delta = \frac{\epsilon}{3} \). Alors, \( |f(x) – f(y)| = |3x + 7 – (3y + 7)| = 3|x – y| \). Si \( |x – y| < \delta \), alors \( 3|x – y| < 3\delta = \epsilon \).
Exercice 2
Montrer que la fonction \( f(x) = x^2 \) n’est pas uniformément continue sur \( \mathbb{R} \).
Pour démontrer que \( f(x) = x^2 \) n’est pas uniformément continue sur \( \mathbb{R} \), nous utilisons un raisonnement par l’absurde en supposant que \( f \) est uniformément continue sur \( \mathbb{R} \). Si \( f \) est uniformément continue, alors pour tout \( \epsilon > 0 \), il existe un \( \delta > 0 \) tel que pour tous \( x, y \in \mathbb{R} \), si \( |x – y| < \delta \), alors \( |x^2 – y^2| < \epsilon \). Considérons \( |x^2 – y^2| = |x+y||x-y| \). Pour des valeurs de \( x \) et \( y \) telles que \( x \) est grand et \( y = x + \delta/2 \), l’expression devient \( |(2x + \delta/2)\delta/2| \). Prenons \( x \) suffisamment grand pour que cette expression dépasse \( \epsilon \), quelle que soit la valeur de \( \delta \). Par exemple, choisissons \( x \) tel que \( 2x > \frac{2\epsilon}{\delta} \), ce qui est toujours possible puisque \( x \) peut être arbitrairement grand. Ainsi, nous avons :
\[
|(2x + \delta/2)\delta/2| = |2x\delta/2 + (\delta/2)^2| = x\delta + \frac{\delta^2}{4}
\]
Pour \( x \) grand, \( x\delta \) deviendra plus grand que \( \epsilon \), peu importe la valeur de \( \delta \), contredisant l’hypothèse que \( \epsilon \) pouvait être rendu arbitrairement petit par rapport aux écarts entre \( x \) et \( y \).
Ainsi, la fonction \( f(x) = x^2 \) ne peut pas être uniformément continue sur \( \mathbb{R} \), car pour des valeurs élevées de \( x \), même des changements très petits dans \( x \) (inférieurs à \( \delta \)) peuvent entraîner des changements significativement grands dans \( f(x) \) qui dépassent \( \epsilon \), ce qui ne respecte pas la définition de la continuité uniforme.
Conclusion
La continuité uniforme est un outil puissant en analyse, offrant une compréhension plus fine des comportements des fonctions sur divers domaines. Sa compréhension est essentielle pour les étudiants qui préparent les épreuves parisiennes et les oraux de mathématiques, permettant de mieux modéliser et prévoir les comportements de fonctions.
Pour t’entraîner et approfondir tes connaissances sur la continuité tu peux réaliser les sujets mathématiques approfondies suivants :
Tu peux retrouver ici toutes nos autres ressources mathématiques !