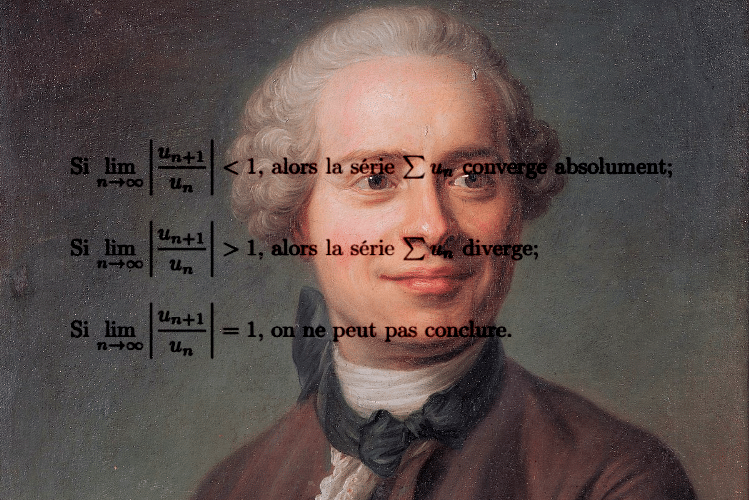Les notions hors programme sont à travailler en priorité par les candidats visant les trois Parisiennes. Cet article te propose de découvrir le critère de d’Alembert, assez récurrent dans les sujets de concours, pour mieux t’aider à le comprendre et d’y d’être sensibilisé(e) afin de ne pas être pris(e) au dépourvu le jour J. Cela te simplifie également la tâche pour ficher.
Le critère de d’Alembert expliqué simplement
Le critère de d’Alembert est un test de convergence qui permet de déterminer la nature des séries à termes positifs.
Il s’avère en particulier très utile lorsque le terme général de la série étudiée contient des factoriels ou des puissances.
Définition du critère de d’Alembert
Soit \( \left(u_{n}\right) \) une suite réelle qui ne s’annule pas à partir d’un certain rang, telle que la suite \( \left( \displaystyle\frac{ |u_{n+1}| }{ |u_{n}| } \right) \) admette une limite finie \(l \in \mathbb{R}^{*}_{+} \).
- Si \( l<1\), alors la série \( \sum{u_{n}} \) converge absolument ;
- Si \( l>1\), alors la série \( \sum{u_{n}} \) diverge ;
- Si \( l=1\), on ne peut pas conclure.
Démonstration
Idée derrière la démonstration
On va chercher à comparer la série \( \sum{u_{n}} \) à une autre série dont on connaît le comportement.
Or, par la définition de la limite, on sait que :
\[ \forall \epsilon > 0, \ \exists n_{0} \in \mathbb{N}, \ \forall n \ge n_{0}, \ l – \epsilon \le \frac{ u_{n+1} }{ u_{n}} \le l + \epsilon . \]
C’est-à-dire
\[ \forall \epsilon > 0, \ \exists n_{0} \in \mathbb{N}, \ \forall n \ge n_{0}, \ \left( l – \epsilon \right)^{n-n_{0}}u_{n_{0}} \le \frac{ u_{n+1} }{ u_{n}} \le \left( l + \epsilon \right)^{n-n_{0}}u_{n_{0}} . \]
C’est-à-dire
\[ \forall \epsilon > 0, \ \exists n_{0} \in \mathbb{N}, \ \forall n \ge n_{0}, \ \left( l – \epsilon \right)^{n}\displaystyle\frac{u_{n_{0}}}{\left( l – \epsilon \right)^{n_{0}}} \le \frac{ u_{n+1}}{ u_{n}} \le \left( l + \epsilon \right)^{n}\displaystyle\frac{u_{n_{0}}}{\left( l – \epsilon \right)^{n_{0}}} . \]
On va donc chercher à comparer \( \left( u_{n} \right) \) avec les suites géométriques \( \left( \left( l – \epsilon \right)^{n} \right) \) et \( \left( \left( l + \epsilon \right)^{n} \right) \).
Préliminaire
On sait que : \( \displaystyle\lim_{n \to \infty}\displaystyle\frac{ |u_{n+1}| }{ |u_{n}|}=l\), avec \(l<1\).
On en déduit que :
\[ \forall \epsilon > 0, \ \exists n_{0} \in \mathbb{N}, \ \forall n \ge n_{0}, \ \bigg| \frac{ u_{n+1} }{ u_{n}} – l \bigg| \le \epsilon . \]
Ce qu’on peut aussi écrire :
\[ \forall \epsilon > 0, \ \exists n_{0} \in \mathbb{N}, \ \forall n \ge n_{0}, \ l – \epsilon \le \frac{ u_{n+1} }{ u_{n}} \le l + \epsilon . \]
Cas où \(l<1\)
Soit \( \epsilon \in \mathbb{R} \) tel que \( l + \epsilon < 1 \). On pose \( l + \epsilon = K \).
On remarque que :
\[ \forall n \ge n_{0}, \ \bigg| \frac{ u_{n+1} }{ u_{n}} \bigg| \le K \Leftrightarrow \ | u_{n+1}| \le K | u_{n}|. \]
Première méthode : Récurrence
Montrons par récurrence que, pour tout entier \( n \ge n_{0} \), la propriété \( \mathscr{P}_{n} \ : “ \ |u_{n}| \le C \cdot K^{n}, \text{ avec } C=\displaystyle\frac{|u_{n_{0}}|}{K^{n_{0}}}” \) est vraie.
Initialisation
\( \displaystyle\frac{|u_{n_{0}}|}{K^{n_{0}}} \cdot K^{n_{0}} = |u_{n_{0}}| \). Ainsi, \( \mathscr{P}_{n_{0}} \) est vraie.
Hérédité
Supposons \( \mathscr{P}_{n} \) vraie pour un entier \( n \ge n_{0} \) fixé. Il vient alors que : \(| u_{n}| \le C \cdot K^{n} \). Or, on sait que : \( | u_{n+1}| \le K | u_{n}| \). Donc \( | u_{n+1}| \le K \cdot C \cdot K^{n} \). i.e. \(| u_{n+1}| \le C \cdot K^{n+1} \). Ainsi, \( \mathscr{P}_{n+1} \) est vraie.
Conclusion
Ainsi, par le principe de récurrence, la propriété \( \mathscr{P}_{n} \) est vraie pour tout entier \( n \ge n_{0} \), donc :
\[ \forall n \ge n_{0}, \ |u_{n}| \le C \cdot K^{n}, \text{ avec } C=\displaystyle\frac{|u_{n_{0}}|}{K^{n_{0}}} \]
Or, la série \( \displaystyle\sum_{n \ge 0}{K^{n}} \) converge en tant que série géométrique car \( K \in ]0,1[ \).
Ainsi, la série \( \displaystyle\sum_{n \ge n_{0}}{K^{n}} \) converge.
Par comparaison de séries à termes positifs, la série \( \displaystyle\sum_{n \ge n_{0}}{|u_{n}|} \) converge.
Donc, la série \( \displaystyle\sum_{n \ge 0}{|u_{n}|} \) converge, et donc la série \( \displaystyle\sum_{n \ge 0}{u_{n}} \) converge absolument.
On vient ainsi de montrer que :
\[ \fbox{\( \text{Si } l<1\text{ , alors la série } \sum{u_{n}} \text{ converge absolument } \)} \]
Seconde méthode : Faire intervenir une suite décroissante à partir d’un certain rang
\( \begin{align} \forall n \ge n_{0} \ : \ \bigg| \displaystyle\frac{ u_{n+1} }{ u_{n}} – l \bigg| \ge K & \Leftrightarrow \displaystyle\frac{|u_{n+1}|}{K} \le |u_{n}| \\ & \Leftrightarrow \displaystyle\frac{|u_{n+1}|}{K^{n+1}} \le \frac{|u_{n}|}{K^{n}} \end{align} \)
Posons la suite \( \left( v_{n} \right) \), telle que : \( \forall n \in \mathbb{N}, \ v_{n} = \displaystyle\frac{|u_{n}|}{K^{n}}. \)
Il vient alors :
\[ \forall n \ge n_{0}, \ v_{n+1} \le v_{n}, \textit{ i.e. } \forall n \le n_{0}, \ v_{n} \ge v_{n_{0}} \]
Il vient donc que :
\[ \forall n \le n_{0}, \ |u_{n}| \le v_{n_{0}} \cdot K^{n} \]
Or, la série \( \displaystyle\sum_{n \ge 0}{K^{n}} \) converge en tant que série géométrique car \( K \in ]0,1[ \).
Ainsi, la série \( \displaystyle\sum_{n \ge n_{0}}{K^{n}} \) converge, et, par comparaison de séries à termes positifs, la série \( \displaystyle\sum_{n \ge n_{0}}{|u_{n}|} \) converge, et donc la série \( \displaystyle\sum_{n \ge 0}{|u_{n}|} \) converge, et donc la série \( \displaystyle\sum_{n \ge 0}{u_{n}} \) converge absolument.
On vient ainsi de montrer que :
\[ \fbox{\( \text{Si } l<1\text{ , alors la série } \sum{u_{n}} \text{ converge absolument } \)} \]
Cas où \(l>1\)
Soit \( \epsilon > 0 \) tel que \( l – \epsilon > 1 \). On pose \( l – \epsilon = K \).
On sait que :
\[ \forall n \le n_{0}, \ \bigg| \frac{ u_{n+1} }{ u_{n}} \bigg| \le K. \]
Et donc que :
\[ \forall n \le n_{0}, \ |u_{n+1}| \ge K \cdot |u_{n}| \ge |u_{n}|.\]
On en déduit que :
\[ \forall n \le n_{0}, \ |u_{n}| \ge |u_{n_{0}}| \ge 0.\]
Et donc, la suite \( \left( u_{n} \right) \) ne tend pas vers \( 0 \) et la série \( \sum{u_{n}} \) diverge grossièrement.
On vient ainsi de montrer que :
\[ \fbox{\( \text{Si } l>1\text{ , alors la série } \sum{u_{n}} \text{ diverge } \)} \]
Cas où \(l=1\)
Soit \( \alpha \in \mathbb{R} \).
Considérons la suite \( \left( u_{n} \right)_{n \in \mathbb{N}^{*}} \), définie comme suit : \( \forall n \in \mathbb{N}^{*}, \ u_{n} = \frac{1}{n^{ \alpha }} \).
\( \displaystyle\frac{u_{n+1}}{u_{n}}=\displaystyle\frac{n^{ \alpha }}{ \left( n+1 \right)^{ \alpha }} \displaystyle\underset{+ \infty }{ \sim } \frac{n^{ \alpha }}{n^{ \alpha }}=1 \).
Ainsi, \( \displaystyle\lim_{n \to +\infty}{\displaystyle\frac{u_{n+1}}{u_{n}}}=1 \)
Or, la série de Riemann \( \sum{u_{n}} \) converge si \( \alpha > 1 \) et diverge si \( \alpha \le 1 \).
On vient de montrer \( l = 1 \) n’implique pas nécessairement que la série \( \sum{u_{n}} \) converge ou diverge.
On vient ainsi de montrer que :
\[ \fbox{\( \text{Si } l=1\text{ , alors la série on ne peut conclure.} \)} \]
Exercices d’application
Je te propose en synthèse des exemples d’application du critère de d’Alembert. Je t’encourage à les faire par toi-même avant de regarder la correction.
Énoncé
En appliquant le critère de d’Alembert, étudier la convergence des séries suivantes :
- \( \displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{n}{e^{n}}}; \)
- \( \displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{n}{e^{n}}}; \)
- \( \displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{4^{n}\left( n+1\right)^{2}}{n!}}. \)
Correction
- \( \forall n \in \mathbb{N}^{*}, \displaystyle\frac{\frac{n+1}{e^{n+1}}}{\frac{n}{e^{n}}}=\displaystyle\frac{n+1}{n} \cdot \displaystyle\frac{1}{e} \) et \( \displaystyle\frac{n+1}{n} \cdot \displaystyle\frac{1}{e} \displaystyle\underset{n \to +\infty}{\to} \displaystyle\frac{1}{e} < 1\). Ainsi, d’après le critère de d’Alembert, la série \( \displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{n}{e^{n}}} \) converge absolument.
- De même, \( \displaystyle\lim_{n \to \infty}\displaystyle\frac{\frac{n+1}{e^{n+1}}}{\frac{n}{e^{n}}}=e>1 \). Ainsi, d’après le critère de d’Alembert, la série \(\displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{n}{e^{n}}}\) diverge.
- \( \displaystyle\frac{\frac{4^{n+1}\left( n+2\right)^{2}}{(n+1)!}}{\frac{4^{n}\left( n+1\right)^{2}}{n!}}=\displaystyle\frac{4^{n+1}\left( n+2\right)^{2}}{(n+1)!}\cdot\frac{n!}{4^{n}\left( n+1\right)^{2}}=\displaystyle\frac{4\left( n+2\right)^{2}}{\left( n+1\right)^{3}}\displaystyle\underset{n \to +\infty}{\to} 0.\) Ainsi, d’après le critère de d’Alembert, la série \( \displaystyle\sum_{n \in \mathbb{N}^{*}}{\displaystyle\frac{4^{n}\left( n+1\right)^{2}}{n!}} \) converge absolument.
N’hésite pas à consulter tous nos articles de mathématiques !