Dans cet article, tu trouveras les démonstrations des formules trigonométriques qu’il faudra connaître pour les concours. En effet, cela pourrait être utile pour éviter de toutes les apprendre par cœur (et donc de perdre du temps, sans oublier le risque de te tromper), car elles se retrouvent facilement, en n’en connaissant que cinq !
Attention, cet article est réservé aux maths approfondies, les fonctions trigonométriques n’étant pas au programme des maths appliquées.
Petits rappels des formules trigonométriques
Pour en savoir plus sur les fonctions trigonométriques, je t’invite à consulter cet article.
Dans tout l’article, on prend \(a\) et \(b\) deux réels.
Les valeurs à connaître
Voici un tableau récapitulatif à connaître par cœur :
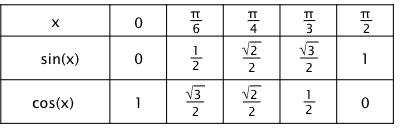
Les formules trigonométriques à connaître
Ces cinq formules classiques sont à connaître par cœur. Elles vont te servir pour retrouver celles que je vais démontrer juste en dessous.
- \(\cos^{2}(a)+\sin^{2}(a)=1\)
- \(\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\)
- \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\)
- \(\sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)\)
- \(\sin(a-b)=\cos(a)\sin(b)-\cos(b)\sin(a)\)
Démonstration des autres formules trigonométriques
cos(2a) et sin(2a)
- Montrons que \(\cos(2a)=2\cos^{2}(a)-1=1-2\sin^{2}(a)\)
\(
\begin{align}
\cos(2a)&=\cos(a+a)\\
&=\cos(a)\cos(a)-\sin(a)\sin(a)\\
&=\cos^{2}(a)-\sin^{2}(a)\\
&=cos^{2}(a)-(1-\cos^{2}(a))\\
&=2\cos^{2}(a)-1
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \cos(2a)=2\cos^{2}(a)-1\)}\]
De la même manière :
\(
\begin{align}
\cos(2a)&=\cos(a+a)\\
&=\cos(a)\cos(a)-\sin(a)\sin(a)\\
&=\cos^{2}(a)-\sin^{2}(a)\\
&=(1-\sin^{2}(a))-\sin^{2}(a)
&=1-2\sin^{2}(a)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \cos(2a)=1-2\sin^{2}(a)\)}\]
- Montrons que \(\sin(2a)=2\sin(a)\cos(a)\)
\(
\begin{align}
\sin(2a)&=\sin(a+a)\\
&=\sin(a)\cos(a)+\cos(a)\sin(a)\\
&=2\sin(a)\cos(a)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \sin(2a)=2\sin(a)\cos(a)\)}\]
Transformations trigonométriques de produits en sommes (démonstration)
Ces formules peuvent être très utiles, notamment lorsqu’il faut calculer une intégrale.
- Montrons que \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\)
D’après le cours, \(\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\) et \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\).
En additionnant ces deux égalités, on a :
\(2\cos(a)\cos(b)=\cos(a+b)+\cos(a-b)\)
D’où \[ \fbox{\( \displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a+b)+\cos(a-b)\)}\]
- Montrons que \(\displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b))\)
D’après le cours, \(\displaystyle \cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)\) et \(\cos(a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\).
En soustrayant :
\(
\begin{align}
\cos(a-b)-\cos(a+b)&=(\cos(a)\cos(b)+\sin(a)\sin(b))-(\cos(a)\cos(b)-\sin(a)\sin(b))\\
&=2\sin(a)\sin(b)
\end{align}
\)
D’où \[ \fbox{\( \displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b)\)}\]
- Montrons que \(\displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b))\)
D’après le cours, \(\displaystyle \sin(a+b)=\cos(a)\sin(b)+\cos(b)\sin(a)\) et \(\sin(a-b)=\cos(a)\sin(b)-\cos(b)\sin(a)\).
En additionnant ces deux égalités, on a :
\(2\sin(a)cos(b)=\sin(a+b)+\sin(a-b)\)
D’où \[ \fbox{\( \displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b)\)}\]
Formules trigonométriques de linéarisation (démonstration)
- Montrons que \(\displaystyle \cos^{2}(a)=\frac{1}{2}(1+\cos(2a))\)
D’après la démonstration précédente, \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\).
D’où :
\(\displaystyle \cos(a)\cos(a)=\frac{1}{2}(\cos(a-a)+cos(a+a))\)
\(\Leftrightarrow\)
\(\cos^{2}(a)=\frac{1}{2}(\cos(0)+\cos(2a))\)
D’où, finalement, \[ \fbox{\( \displaystyle \cos^{2}(a)=\frac{1}{2}(1+\cos(2a))\)}\]
- De la même manière, on montre que
\[ \fbox{\( \displaystyle \sin^{2}(a)=\frac{1}{2}(1-\cos(2a))\)}\]
Transformation trigonométriques de sommes en produits (démonstration)
Dans un exercice, comme dans HEC 2018, les formules suivantes seront données, et tu devras les démontrer. On part alors d’un côté de l’équation pour prouver l’égalité.
- Montrons que \(\displaystyle \cos(a)+\cos(b)=2\cos(\frac{a+b}{2})\cos(\frac{a-b}{2})\)
On sait que \(\displaystyle \cos(a)\cos(b)=\frac{1}{2}(\cos(a-b)+cos(a+b))\)
En remplaçant \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\displaystyle \frac{a-b}{2}\) dans l’égalité précédente, on a :
\(\displaystyle \cos(\frac{a+b}{2})\cos(\frac{a-b}{2})=\frac{\cos(\frac{a+b}{2}+\frac{a-b}{2})+\cos(\frac{a+b}{2}-\frac{a-b}{2})}{2}\)
En simplifiant, on obtient :
\(\displaystyle \cos(\frac{a+b}{2})+\cos(\frac{a-b}{2})=\frac{\cos(a)+\cos(b)}{2}\)
D’où, finalement : \[ \fbox{\( \displaystyle 2\cos(\frac{a+b}{2})+\cos(\frac{a-b}{2})=\cos(a)+\cos(b) \)}\]
- Montrons que \(\displaystyle \cos(a)-\cos(b)=-2\sin(\frac{a+b}{2})\sin(\frac{a-b}{2})\)
On sait que \(\displaystyle \sin(a)\sin(b)=\frac{1}{2}(\cos(a-b)-\cos(a+b))\)
En remplaçant \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\frac{a-b}{2}\) dans l’égalité précédente, on a :
\(\displaystyle \sin(\frac{a+b}{2})\sin(\frac{a-b}{2})=\frac{\cos(\frac{a+b}{2}-\frac{a-b}{2})-\cos(\frac{a+b}{2}+\frac{a-b}{2})}{2}\)
En simplifiant, on obtient :
\(\displaystyle \sin(\frac{a+b}{2})\sin(\frac{a-b}{2})=\frac{\cos(b)-\cos(a)}{2}\)
D’où \[ \fbox{\( \displaystyle \cos(a)-\cos(b)=-2\sin(\frac{a+b}{2})\sin(\frac{a-b}{2})\)}\]
- Montrons que \(\displaystyle \sin(a)+\sin(b)=2\sin(\frac{a+b}{2})\cos(\frac{a-b}{2})\)
On sait que \(\displaystyle \sin(a)\cos(b)=\frac{1}{2}(\sin(a-b)+\sin(a+b))\)
De la même manière que les démonstrations précédentes, on remplace \(a\) par \(\displaystyle \frac{a+b}{2}\) et \(b\) par \(\frac{a-b}{2}\) dans l’égalité et on obtient :
\[ \fbox{\( \displaystyle\sin(a)+\sin(b)=2\sin(\frac{a+b}{2})\cos(\frac{a-b}{2})\)}\]
- Montrons que \(\displaystyle \sin(a)-\sin(b)=2\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})\)
De la même façon que dans les démonstrations précédentes, on trouve
\[ \fbox{\( \displaystyle\sin(a)-\sin(b)=2\cos(\frac{a+b}{2})\sin(\frac{a-b}{2})\)}\]
La trigonométrie expliquée dans une vidéo très complète
Si des paroles sont mieux que des mots pour ta compréhension de la trigonométrie, on t’invite à aller voir cette merveilleuse vidéo explicative de Ambroise réalisée sur notre chaîne youtube, il détaille vraiment tout sur tout de la trigonométrie dans les moindres détails…
Les sujets en rapport avec les formules de trigonométrie
Avec ça tu pourras performer au concours sur les formules de trigo. Je te conseille de faire aussi des annales à fond :
Et il y a encore bien d’autres annales traitant de ces formules de trigo.
Aller plus loin
Les fonctions de trigonométries peuvent être approfondies sous différentes formes. En effet, les fonctions sinus et cosinus ont donné lieu à de nombreuses notions hors programme (qui se trouvent régulièrement dans les sujets). Parmi elles, tu peux retrouver : voici un tableau récapitulatif de toutes nos ressources de trigonométrie sur Major Prépa, que ce soit aussi bien en termes de notions de cours comme de notions hors programme :
| Contenu de trigonométrie au programme et hors programme ECG | |
| Trigo au programme | Trigo hors programme |
| Tout sur les fonctions de trigonométrie cos et sin | Les fonctions de trigonométrie cosh et sinh (cosinus hyperbolique et sinus hyperbolique) |
| Fiche récapitulative des formules de trigo | Trigonométrie et nombres complexes |
| Démonstrations des formules trigonométriques | La loi arcsinus standard et à support borné |
| Zoom sur la fonction Arctangente (Arctan et toutes ses méthodes associées) | Les intégrales de Wallis |
| Vidéo explicative de la trigonométrie | L’intégrale de Dirichelet |
| La trigonométrie (du point de vue du lycée, trigo troisième, trigonométrie en seconde…) | Transformée de Fourier (mais il y a des nombres complexes…) |
| Tout comprendre sur le cercle trigonométrique | |
J’espère que cet article t’aura plu, te voici maintenant pro en trigonométrie ! N’hésite pas à consulter toutes nos ressources en mathématiques.













