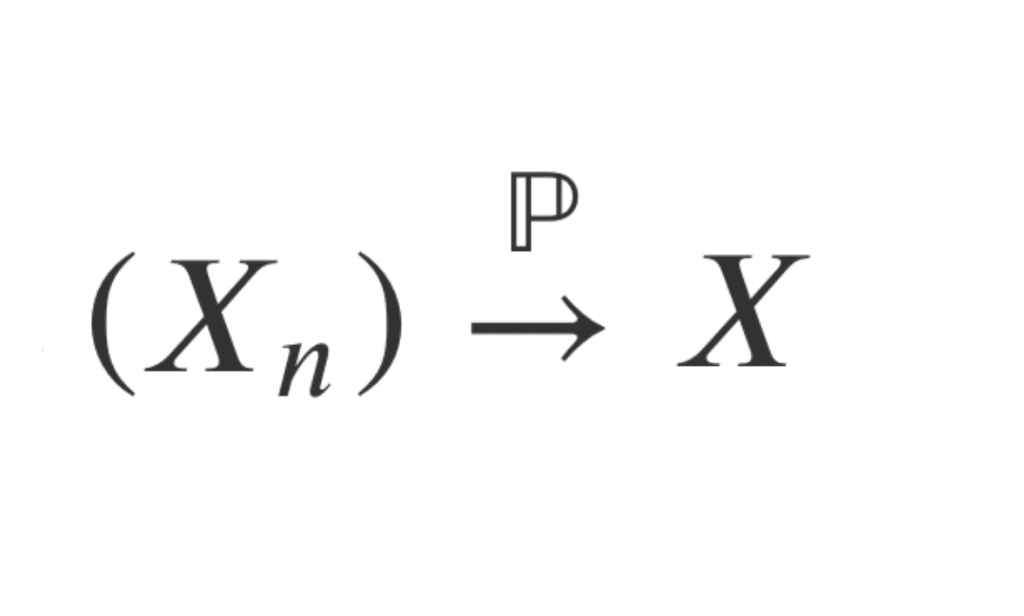Le chapitre de probabilité sur les convergences arrive assez tardivement dans l’année d’un préparationnaire. Il peut alors arriver que son traitement soit expéditif. C’est dommage, car les questions qui traitent de convergence, en plus d’être intéressantes, se traitent généralement de la même manière. Elles peuvent donc être assez faciles à aborder lorsque l’on y est habitué.
Je te propose donc de découvrir quelques méthodes pour résoudre ces questions de convergence.
La convergence en probabilité
Définition
Soit \((X_n)_{n \in \mathbb{N}}\) une suite de variables aléatoires et \(X\) une variable aléatoire. On dit que ( \(X_n)_{n \in \mathbb{N}}\) converge en probabilité vers \(X\) lorsque :
\(\forall \epsilon >0, \lim \limits_{n \to +\infty} P(|X_n-X|> \epsilon)=0\)
On note alors \( (X_n) \overset{\mathbb{P}}{\rightarrow} X\)
Les outils du cours dont on dispose
Certains résultats du cours sont très utiles pour démontrer une convergence en probabilité. Le premier étant la loi faible des grands nombres.
Soit \( (X_n)_{n \in \mathbb{N}^*}\) une suite de variables aléatoires indépendantes, possédant une même espérance notée \(m\) et la même variance \(\sigma^2\). Alors \(( \displaystyle \frac{1}{n} \sum_{k=1}^n X_k)\) converge en probabilité vers \(m\).
Si tu retrouves ces hypothèses, il n’y a alors aucune hésitation à avoir. Il suffit d’appliquer la loi faible des grands nombres.
Les autres outils principaux sont ce qu’on appelle les inégalités de concentration (Markov et Bienaymé-Tchebychev).
Inégalité de Markov
Soit \(X\) une variable aléatoire positive possédant une espérance.
Alors : \(\forall a >0, P(X \ge a) \le \frac{E(X)}{a}\)
Inégalité de Bienaymé-Tchebychev
Soit \(X\) une variable aléatoire possédant une variance (et donc aussi une espérance).
\(\forall \epsilon >0, P(|X-E(X)| \ge \epsilon) \le \frac{V(X)}{\epsilon^2}\)
Utiliser les inégalités de concentration pour démontrer des convergences en probabilité
L’inégalité de Markov
Considérons une suite \((X_n)\) de variables aléatoires et \(X\) une variable aléatoire.
- Si dans l’énoncé, il est indiqué que \(\lim \limits_{n \to +\infty} E(|X_n-X|)=0 \)
Alors, tu peux appliquer l’inégalité de Markov à la variable aléatoire \(|X_n-X|\) (qui est bien positive). On a alors :
\(\forall a >0, P(|X_n-X|\ge a) \le \frac{E(|X_n-X|)}{a}\)
Or, par définition, une probabilité est positive, donc par théorème d’encadrement, on a :
\(\forall a>0 \lim \limits_{n \to +\infty} P(|X_n-X| \ge a)=0\)
D’où : \( (X_n) \overset{\mathbb{P}}{\rightarrow} X\)
- Si dans l’énoncé, il est indiqué que \(\lim \limits_{n \to +\infty} E((X_n-X)^2)=0 \), tu peux raisonner comme précédemment, en appliquant cette fois-ci l’inégalité de Markov à la variable aléatoire positive \((X_n-X)^2\)
On a donc de même que précédemment, par encadrement : \(\forall a>0 \lim \limits_{n \to +\infty} P((X_n-X)^2 \ge a)=0\)
Or, dans la mesure où la fonction carrée est bijective croissante de \(\mathbb{R}_+\) dans \(\mathbb{R}_+\), on a :
\(P((X_n-X)^2 \ge a)= P(|X_n-X| \ge \sqrt(a))\)
En notant \(\epsilon= \sqrt a\), on a alors : \(\forall \epsilon >0, \lim \limits_{n \to +\infty} P(|X_n-X| \ge \epsilon)=0\)
Par définition, on a alors bien \( (X_n) \overset{\mathbb{P}}{\rightarrow} X\)
L’inégalité de Bienaymé-Tchebychev
Soit \((X_n)\) une suite de variables aléatoires possédant une même espérance notée \(m\) et une variance qui tend vers 0.
Si on te demande de montrer que \((X_n)\) converge en probabilité vers \(m\), tu peux alors appliquer l’inégalité de Bienaymé-Tchebychev à la variable \(X_n\).
Soit \(n \in \mathbb{N}\), Soit \(\epsilon >0, P(|X_n-m| \ge \epsilon) \le \frac{V(X_n)}{\epsilon^2}\)
Alors, par encadrement : \(\forall \epsilon>0 \lim \limits_{n \to +\infty} P(|X_n-m| \ge \epsilon)=0\)
D’où : \( (X_n) \overset{\mathbb{P}}{\rightarrow} m\)
La convergence en loi
Définition
Soit \((X_n)\) une suite de variables aléaoires, \(F_n\) les fonctions de répartition qui leur sont associées, \(X\) une variable aléatoire, et \(F_X\) sa fonction de répartition.
On dit que \((X_n\)) converge en loi vers \(X\), et on note alors \( (X_n) \overset{\mathcal{L}} {\rightarrow} X\) lorsque pour tout \(x\) de \(\mathcal{C}\) (où \(\mathcal{C}\) désigne l’ensemble des points en lesquels la fonction \(F_X\) est continue) : \(\lim \limits_{n \to +\infty} F_n(x)=F_X(x)\)
Il est important de signaler que la relation \(\lim \limits_{n \to +\infty} F_n(x)=F_X(x)\) est demandée seulement sur \(\mathcal{C}\), et non sur \(\mathbb{R}\) tout entier.
Démontrer une convergence en loi
Le cas où les variables \(X_n\) et \(X\) sont discrètes
Ce cas est particulier, car pour démontrer que la suite \((X_n)\) converge en loi vers \(X\), il suffit de montrer que la convergence est vérifiée pour les atomes, c’est-à-dire :
\(\forall x \in X(\Omega), \lim \limits_{n \to +\infty} P(X_n=x)=P(X=x)\)
Pas besoin de passer par les fonctions de répartition donc.
Les autres cas
Si tu n’es pas dans ce cas, pas le choix. Il faut déterminer les fonctions de répartition \(F_n\) et \(F_X\), à partir d’une densité dans la plupart des cas. Puis, montrer que pour les points où \(F_X\) est continue \(\lim \limits_{n \to +\infty} F_n(x)=F_X(x)\)
C’est ce point en gras dont il faut ce souvenir, car il nous préserve d’étudier tout un tas de cas dégénérés et simplifie considérablement le travail.
Conclusion
Tu l’auras compris, ces questions ne sont généralement pas difficiles dans les concepts. Tu seras donc attendu·e au tournant sur la rigueur, les justifications et la maîtrise de ton cours et de ses hypothèses. Il ne faut donc absolument pas bâcler ces questions.
Pour consulter toutes nos ressources en maths, ça se passe ici !