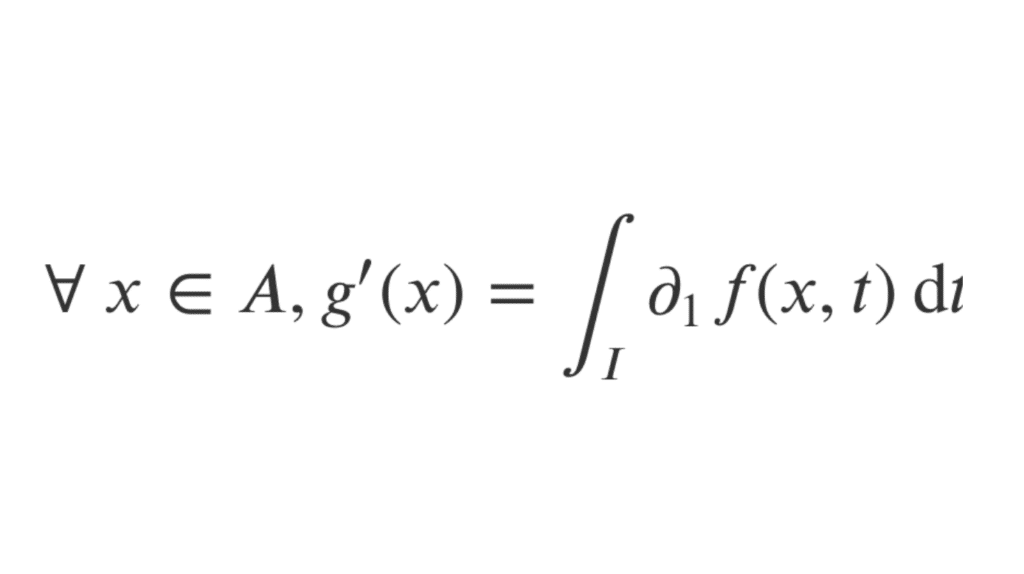ATTENTION : Petite remarque avant de traiter du théorème de Leibniz. Cet article traite de la dérivation sous le signe de l’intégrale, qui est une notion hors programme. Tu ne pourras donc pas l’utiliser de toi-même aux écrits (sauf s’il s’agit du thème du sujet). Les correcteurs attendent de toi une autre méthode de résolution.
Cependant, lors des oraux, les examinateurs laissent souvent les candidats utiliser des théorèmes hors programme s’ils les connaissent. Il faut néanmoins t’attendre à quelques questions ayant pour but de vérifier que tu maîtrises bien ce dont tu parles !
Pour utiliser ce théorème, il est nécessaire d’avoir vu au préalable le chapitre sur les fonctions à plusieurs variables.
Il doit t’être déjà arrivé, lors d’exercices, de vouloir dériver des intégrales. Cependant, ton professeur a déjà dû te mentionner que la dérivée d’une intégrale n’est pas l’intégrale d’une dérivée ! La réalité est un peu plus complexe, mais la méthode n’en reste pas moins plutôt simple.
Dans cet article, je te détaille pas à pas le théorème de Leibniz, qui permet de dériver une intégrale, et je te propose une mise en application rapide, afin que tu intègres la façon de procéder du mieux possible.
Théorème de Leibniz
On considère \(A\) et \(I\) deux intervalles de \(\mathbb{R}\) et \(f\) une fonction définie sur \(A \times I\) à valeurs dans \(\mathbb{C}\) (le fait que \(f\) prenne ses valeurs dans \(\mathbb{C}\) fait que le théorème marche également pour des fonctions qui prennent leurs valeurs dans \(\mathbb{R}\)).
On suppose que :
- \( \forall x \in A, t \mapsto f(x,t)\) est continue par morceaux et intégrable sur \(I\).
- \(\forall t \in I, x \mapsto f(x,t)\) est de classe \(C^1\) sur \(A\).
- \(\forall x \in A, t \mapsto \partial_{1} f(x,t)\) est continue par morceaux.
- Il existe une fonction \(\phi\) INDÉPENDANTE DE \(x\) continue par morceaux et intégrable sur \(I\) telle que :
\[ \forall(x,t) \in a \times I, |\partial_{1} f(x,t)| \le \phi(t)\]
\[ \fbox{\( \text{Alors} \ g : x \mapsto \displaystyle \int_I f(x,t)\, \mathrm{d}t \ \text {est de classe} \ C^1 \text{ sur A et}\ \forall \ x \in A, g'(x) = \displaystyle \int_I \partial _1f(x,t)\, \mathrm{d}t \ \)}\]
Cas particulier
Dans le cas où \( I = [a,b]\) avec \( -\infty < a < b < + \infty\), les théorèmes sont un peu plus simples et deviennent :
- si \(f\) est continue sur \( A \times [a,b]\), alors la fonction \( x \mapsto \displaystyle \int_{a}^{b}f(x,t) \,\mathrm{d}t\) est définie et continue sur \(A\) ;
- si \(f\) est \(C^1\) sur \( A \times [a,b]\), alors \( g : x \mapsto \displaystyle \int_{a}^{b} f(x,t) \, \mathrm{d}t\) est \(C^1\) sur \(A\) et \(\forall x \in A, g'(x) = \displaystyle \int_{a}^{b} \partial_1 f(x,t) \, \mathrm{d}t\).
Exercice d’application
On pose, pour tout \(x \in \mathbb{R}\), \( F(x) = \displaystyle \int_{0}^{+\infty} \frac{sin(xt)}{t}e^{-t} \mathrm{d}t \)
- Justifier que \(F\) est bien définie sur \(\mathbb{R}\)
- Justifier que \(F\) est \(C^1\) et donner une expression de \(F'(x)\) pour tout \(x \in \mathbb{R}\)
Correction
- L’intégrale est faussement impropre pour la borne 0, car la fonction se prolonge par continuité en 0. Ainsi, la fonction \(t \mapsto \displaystyle \frac {sin(xt)}{t}e^{-t}\) est continue sur \([0,+\infty[\) et on a pour tout \(t \ge 1\), \( \left |\displaystyle \frac{sin(xt)}{t}e^{-t} \right | \le e^{-t}\). La fonction \(t \mapsto e^{-t}\) étant intégrable sur \([0,+\infty[\), on en déduit que la fonction \(t \mapsto \displaystyle \frac {sin(xt)}{t}e^{-t}\) est intégrable sur \([0,+\infty[\), et que \(F\) est bien définie sur \(\mathbb{R}\).
- Posons, pour \(x \in \mathbb{R}\) et \(t>0\), \(f(x,t) = \displaystyle \frac {sin(xt)}{t}e^{-t}\).
– Ainsi, pour \(x \in \mathbb{R}\), la fonction \(t \mapsto f(x,t)\) est continue (donc continue par morceaux) et intégrable sur \(\mathbb{R}^*_+\).
– \(\forall t \in \mathbb{R}^*_+\), la fonction \(x \mapsto f(x,t)\) est \(C^1\) sur \(\mathbb{R}\) (théorèmes classiques).
– De plus, pour tout \((x,t) \in \mathbb{R} \times \mathbb{R^*_+}, |\partial_1(f)(x,t)|\le e^{-t}\) et cette dernière fonction est intégrable sur \(\mathbb{R}^*_+\).
On en déduit par le théorème de Leibniz que \(F\) est de classe \(C^1\) sur \(\mathbb{R}\), et que \[ F'(x) = \displaystyle \int_{0}^{+\infty} cos(xt)e^{-t} \mathrm{d}t \]
N’hésite pas à consulter toutes nos ressources mathématiques !