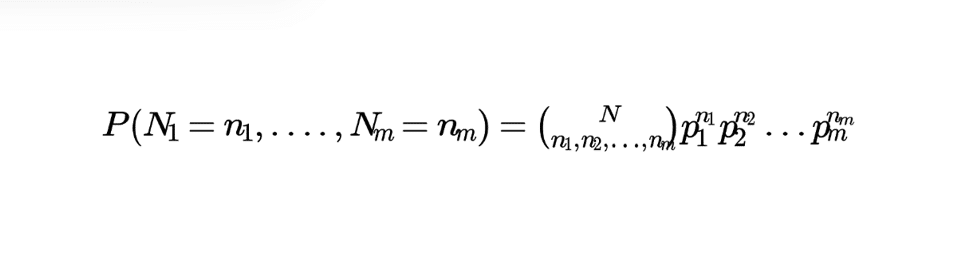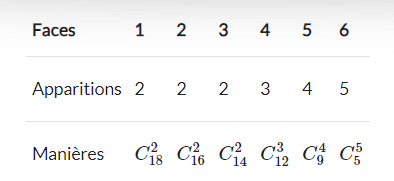Cet article s’intéresse à une loi de probabilité particulière qui généralise la loi binomiale. On vise ici à décortiquer les principales propriétés de la loi multinomiale, qui pourrait tomber dans un sujet de concours, probablement un sujet de Maths II.
Introduction
En théorie des probabilités, la loi multinomiale généralise la loi binomiale. Tandis que la loi binomiale concerne le nombre de succès lors d’une série de \(n\) épreuves de Bernoulli indépendantes, la loi multinomiale ne se restreint pas aux épreuves comportant deux issues.
Par exemple, la loi multinomiale s’applique au cas de \(n\) jets d’un dé à six faces. L’apparition du chiffre 1 seul peut être modélisée par une loi binomiale, alors que l’ensemble des apparitions des faces de 1 à 6 est modélisé par une loi multinomiale.
La loi multinomiale intervient dans de nombreuses branches de la Statistique : schéma probabiliste, théorie des sondages, statistique du khi-deux…
Construction de la loi multinomiale
On prend un dé non truqué et on note \(\pi=(p_1,p_2,…,p_6)\) l’ensemble des probabilités d’apparition de chaque face. On note que \(p_1+p_2+….+p_3=1\).
Supposons qu’on réalise 18 lancers indépendants, on obtient deux 1, deux 2, deux 3, trois 4, 4 cinq et 5 six. Dans cette configuration, la probabilité de cette séquence \(S\) est \(P(S)=p_1^2p_2^2p_3^2p_4^3p_5^4p_6^5\).
Dans la mesure où ce calcul est une multiplication, toute permutation de la séquence précédente aurait la même probabilité d’apparition et ferait apparaître la même séquence observée. Pour obtenir une probabilité complète de cette répartition, tous scénarios confondus, on peut dénombrer le nombre de manières qu’il y a d’y arriver, case par case. On obtient alors ce tableau (à noté : \(C_18^2\) correspond à \({{18}\choose{2}}\)) :
On note que dans ce dénombrement par case, le total dans lequel on prend (nombre en bas) est diminué des observations qu’on a placées dans la case précédente. En multipliant toutes ces possibilités, on trouve que \({{18}\choose{2,2,2,3,4,5}}=C_18^2C_16^2…..C_5^5=46313467200\) séquences de réponses différentes peuvent amener cette distribution.
En les prenant toutes en compte, la probabilité totale de cette distribution particulière est donc \(P(n\pi)={{18}\choose{2,2,2,3,4,5}}p_1^2p_2^2p_3^2p_4^3p_5^4p_6^5\).
Généralisation
D’une façon générale, dans ce type de situation, les données sont des comptages bornés des \(m\) modalités d’une variable catégorisée. Si les conditions suivantes sont réunies :
- les résultats des lancers sont indépendants ;
- la probabilité de tomber sur une issue donnée est toujours la même.
Alors la probabilité d’un ensemble particulier d’effectifs prend la forme suivante, dite loi multinomiale :
En posant les variables \(N_i\) correspondant aux probabilités \(p_i\), on obtient : \(P(N_1=n_1,….,N_m=n_m)={{N}\choose{n_1,n_2,…,n_m}}p_1^{n_1}p_2^{n_2}…p_m^{n_m}\).
Avec l’effectif total \(N=n_1+n_2+…+n_m\).
Propriétés
Chacune des variables \(N_i\) suit une loi binomiale dont l’espérance et la variance sont : \(E(N_i)=np_i\), \(V(N_i)=np_i(1-p_i)\) et les covariances s’écrivent \(Cov(N_i,N_j)=-np_ip_j\) pour \(i \ne j\)
Exemple
\(n\) étudiants votent pour trois candidats pour la présidence de leur BDE. Soit \(X_1,X_2,X_3\) les nombres de votes correspondants, et supposons que les \(n\) étudiants votent indépendamment avec des probabilités \(p_1=0.45\), \(p_2=0.4\) et \(p_3=0.15\).
La loi conjointe de \(X_1,X_2,X_3\) est une loi multinomiale où \(m=3\).
Ainsi \( P(X_1,X_2,X_3)={{n}\choose{x_1,x_2,x_3}}p_1^{x_1}p_2^{x_2}p_3^{x_3}\).
La loi marginale de \(X_3\) est une loi binomiale de paramètre \((n,p_3)\).
La loi multinomiale n’est pas une loi que tu dois maîtriser pour le concours. Cependant, comprendre le mécanisme de dénombrement et le fonctionnement de la loi peut t’être très utile et te permettre de gagner du temps en épreuve !
Tu peux accéder à l’ensemble de nos ressources mathématiques en cliquant ici !