Cet article vise à étudier un type d’endomorphisme bien particulier, les endomorphismes cycliques. Nous verrons les principales propriétés en lien avec ces endomorphismes ainsi que leur liens avec les matrices compagnons. L’étude de ce type d’endomorphisme peut intervenir dans des sujets de tous genres et pour les mathématiques approfondies comme appliquées.
Définition
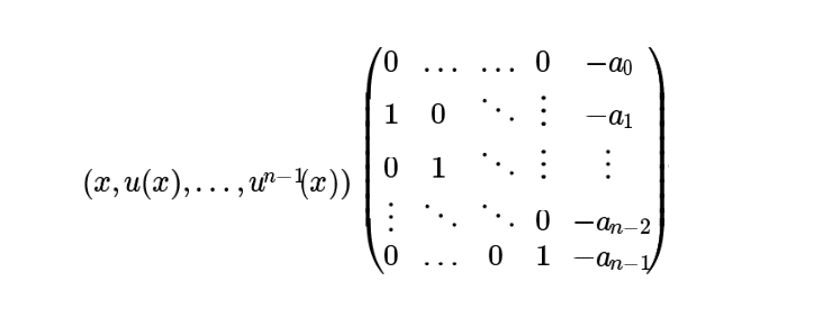
Soit \(E\) un espace vectoriel de dimension finie \(n\) et soit \(u\) un endomorphisme de \(E\). On dit que \(u\) est cyclique s’il existe \(x\) de \(E\) tel que \((x,u(x),…,u^{n-1}(x))\) soit une base de \(E\).
Exemples
Montrons que \(f(x,y)=(4x-2y,x+y)\) est un endomorphisme cyclique en considérant \(v=(1,0)\).
\(f(v)=(4,1)\). Or \((v,f(v))=((1,0),(4,1))\) est une famille libre de \(\mathbb{R}^2\) de dimension \(2\), c’est donc une base. Ainsi \(f\) est un endomorphisme cyclique.
Contre-exemple, soit \(g\) un endomorphisme d’un espace vectoriel de dimension 3 tel que \(g^2=g+2id\). Alors pour tout \(x\), \(g^2(x)=g(x)+2x\). La famille \((x, g(x), g^2(x))\) n’est donc pas libre, donc pas une base. \(g\) n’est alors pas cyclique.
Propriété (en lien avec les matrices de compagnon)
Soit \(u\) un endomorphisme de \(E\). Alors \(u\) est cyclique si et seulement s’il existe une base de \(E\) dans laquelle la matrice de \(u\) est la matrice compagnon du polynôme caractéristique de \(u\).
Autrement dit, \(u\) est cyclique si et seulement s’il existe une base de \(E\) dans laquelle sa matrice est de la forme \(\begin{pmatrix} 0&\dots&\dots&0&-a_0\\ 1&0&\ddots&\vdots&-a_1\\ 0&1&\ddots&\vdots&\vdots\\ \vdots&\ddots&\ddots&0&-a_{n-2}\\ 0&\dots&0&1&-a_{n-1} \end{pmatrix}\).
Pour en savoir plus sur les matrices de compagnon tu peux lire cet article !
Démonstration
Soit \(A=\begin{pmatrix} 0&\dots&\dots&0&-a_0\\ 1&0&\ddots&\vdots&-a_1\\ 0&1&\ddots&\vdots&\vdots\\ \vdots&\ddots&\ddots&0&-a_{n-2}\\ 0&\dots&0&1&-a_{n-1} \end{pmatrix}\) la matrice de \(u\) dans la base \((e_1,…, e_n)\). On a \(u(e_1)=e_2\), \(u^2(e_1)=u(e_2)=e_3\), \(u^3(e_1)=u(e_3)=e_4\) et ainsi de suite jusqu’à \(u^{n-1}(e_1)=u(e_{n-1})=e_n\). Or \((e_1,…,e_n)\) est une base de \(E\) donc \((e_1, u(e_1),…,u^{n-1}(e_1))\) est une base de \(E\) donc \(u\) est cyclique.
Soit \(u\) un endomorphisme cyclique de \(E\) alors il existe \(x\) de \(E\) tel que \((x,u(x),…,u^{n-1}(x))\) soit une base de \(E\). Or \(u^n(x)\) appartient à \(E\) donc il existe une décomposition de \(u^n(x)\) dans la base \((x,u(x),…,u^{n-1}(x))\). Ainsi la matrice de \(u\) dans la base \((x,u(x),…,u^{n-1}(x))\) est une matrice de compagnon.
Exemple :
Soit \(A=\begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & -1 \end{pmatrix}\) la matrice de \(u\) dans la base \((e_1, e_2, e_3)\).
On a \(u(e_1)=e_2\), \(u^2(e_1)=u(e_2)=e_3\) et \((e_1, e_2, e_3)\) qui forment une base donc \((e_1, u(e_1), u^2(e_1))\) forment une base également. \(u\) est donc un endomorphisme cyclique.
Attention erreur classique
Un endomorphisme cyclique peut avoir une représentation matricielle autre qu’une matrice de compagnon.
Par exemple, soit \(e_1,e_2,e_3)\) une base de \(E\) et \(f\) un endomorphisme de \(E\) dont la matrice associé dans cette base est \(A=\begin{pmatrix} 1 &2 &2 \\ 1 & 1 &2\\ -2 & -2 & -3 \end{pmatrix}\).
\(f(e_1)=e_1+e_2-2e_3\) et \(f^2(e_1)=f(e_1+e_2-2e_3)=-e_1-2e_2+2e_3\). On remarque que \((e_1, f(e_1), f^2(e_1))=(e_1, e_1+e_2-2e_3, -e_1-2e_2+2e_3)\) est une famille libre de dimension \(3\) de \(E\) donc une base de \(E\). Ainsi \(f\) est cyclique.
Ainsi une matrice de compagnon représente TOUJOURS un endomorphisme cyclique mais la représentation matricielle d’un endomorphisme cyclique n’est PAS TOUJOURS une matrice de compagnon !
Pour t’entrainer
Pour approfondir et vérifier que tu as bien compris la notion tu peux t’entrainer sur le sujet de mathématiques approfondies de l’EML 2001 (sujet)
N’hésite pas à parcourir toutes nos ressources de mathématiques en cliquant ici !