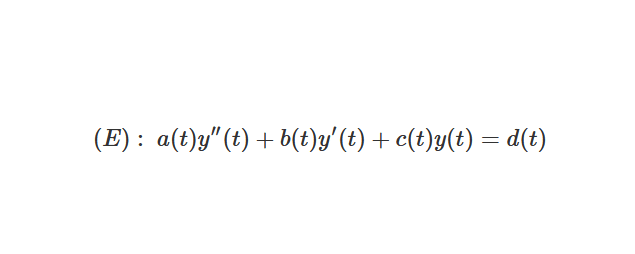Comme tu le sais, les équations différentielles viennent d’entrer au programme en ECG (Maths appliquées). Si le programme s’arrête aux équations différentielles à coefficients constants, tu vas voir que la théorie va bien plus loin, notamment dans le monde des coefficients non constants.
Équations différentielles à coefficients non constants : explication
Soit \( I \) un intervalle de \( \mathbb{R} \), soit \( \mathcal{A}(I, \mathbb{R}) \) l’ensemble des applications de \( I \ \text{dans} \) \( \mathbb{R} \)
Il s’agit donc simplement de faire varier le coefficient \(a\) que tu as l’habitude de voir dans une expression telle que \( (E) : \ y'(t) + ay(t) = b(t) \). En effet ici, tu vois que \( a \in \mathbb{R} \), et ce que nous allons voir aujourd’hui est le cas où \( a \in \mathcal{A}(I, \mathbb{R}) \), c’est-à-dire le cas où \(a\) est une fonction allant de \( I \ \text{dans} \ R \). Il va donc finalement s’agir d’avoir une équation de la forme : \( (E) : \ y'(t) + a(t)y(t) = b(t), \ \text{d’inconnue } y \in \mathcal{A}(I, \mathbb{R}) \)
Cette approche par les coefficients non constants généralise donc celle vue avec des coefficients constants (puisque \( a \in \mathbb{R} \) est une fonction constante). Elle permet aussi de représenter des systèmes plus réalistes (temps, espace) et de modéliser des phénomènes transitoires. Elle a donc toutes les chances de tomber lors d’une prochaine session de concours !
Résolution au premier degré
L’équation homogène
Contrairement à la résolution au second degré, il est assez aisé de transposer ce que l’on sait des équations différentielles à coefficients constants ici. Voici le théorème clé :
Soit \(I\) un intervalle de \(\mathbb{R}\).
On dispose de \(a\) continue sur \(I\) à valeurs dans \(\mathbb{R}\) telle que l’on a :
\( \begin{align*}
(E) : y’ + a(t)y &= b(t) \quad \text{d’inconnue } y \in \mathcal{A}(I, \mathbb{R})
\end{align*} \)
Alors, l’ensemble-solution \(S(E)\) de \((E)\) est donné par :
\[ S(E) = \begin{cases} I \to \mathbb{R} \\ t \mapsto f_p(t) + Ce^{-A(t)}, C \in \mathbb{R}, \ \text{avec} \ A \ \text{une primitive de} \ a \end{cases} \]
N.B. : N’oublie pas de normaliser ton équation différentielle pour pouvoir appliquer ce théorème.
Tu vois donc le parallèle avec le monde constant : l’ensemble solution est de la même forme. On a bien une solution particulière \(t \mapsto f_p(t) \), accompagnée de notre nouvelle solution homogène \(t \mapsto Ce^{-A(t)}\), avec cette fois \(A\) qui est une primitive de \(a\). Tu vois donc qu’à condition de maîtriser tes formules de primitives et d’être à l’aise avec l’intégration, il est aisé de résoudre l’équation homogène. Reste à déterminer une solution particulière.
Une solution particulière
Ici, tu ne peux pas chercher à appliquer les astuces de cet article, propres aux coefficients constants. Ainsi, il faut ici (presque toujours, sauf si tu es aidé(e) par l’énoncé) appliquer la méthode de la variation de la constante (HP), mais en l’adaptant aux coefficients non constants.
Si on reprend l’équation \((E)\) de la section précédente, on peut dire que :
Il existe une fonction \( C \) de classe \( C^{1} \) sur \( I \), telle que \( t \mapsto C(t)e^{-A(t)} \) est solution de \((E)\).
Essayons donc de voir le cas général de résolution sur \( (E) : y’ + a(t)y = b(t) \).
Étape 1
On a notre solution homogène qui est \( \begin{cases} I \to \mathbb{R} \\ t \mapsto Ce^{-A(t)}, C \in \mathbb{R}, \ \text{avec} \ A \ \text{une primitive de} \ a \end{cases} \).
Étape 2
On sait que : \( \forall t \in I, f_p(t) = C(t)e^{-A(t)}, C \in \mathcal{A}(I, \mathbb{R}) \) est une solution de \( (E) \).
2.1 : On a que la dérivée de \( f_p \) (qui est \( C^{1} \) sur \(I\) par produit de deux telles fonctions) est :
\( \begin{align*}
f_p'(t) = C'(t)e^{-A(t)} – C(t)a(t)e^{-A(t)}, \ \text{d’apres la formule de dérivation d’une composée}
\end{align*} \)
2.2 : On substitue \(f_p\) et \(f_p’\) dans \((E) \) et on obtient :
\( \begin{align*}
C'(t)e^{-A(t)} – C(t)a(t)e^{-A(t)} + a(t)C(t)e^{-A(t)} = b(t)
\end{align*} \)
2.3 : En simplifiant et en isolant \( C'(t) \), on a :
\( \begin{align*}
C'(t) = b(t)e^{A(t)}
\end{align*} \)
2.4 : En intégrant \( C'(t) \) par rapport à \( t \), on trouve :
\( \begin{align*}
C(t) = \int b(t)e^{A(t)} dt + C_1, \ \text{ou} \ C_1 \ \text{est une constante d’intégration}
\end{align*} \)
2.5 : La solution particulière est \( f_p(t) = C(t)e^{-A(t)} \), donc :
\( \begin{align*}
f_p(t) = \left( \int b(t)e^{A(t)} dt + C_1 \right) e^{-A(t)}
\end{align*} \)
Étape 3
On peut maintenant écrire notre solution générale en concaténant l’étape 1 et l’étape 2.
\begin{align*}
y(t) = f_h(t) + f_p(t) = Ce^{-A(t)} + \left( \int b(t)e^{A(t)} dt + C_1 \right) e^{-A(t)}, (C,C_1) \in \mathbb{R^2}
\end{align*}
N.B. : Si les étapes 2.4, 2.5 et 3 te paraissent un peu obscures, c’est tout à fait normal. Il n’y a en réalité rien de difficile dans cette généralisation de la variation de la constante, et tu verras qu’en t’entraînant sur quelques cas particuliers, le schéma finira par te paraître naturel.
Un exemple concret
Justement, voyons tout cela sur un exemple concret en résolvant l’équation différentielle \( (E) : y’ + \frac{2}{t}y = t^{2} \ \) sur \( \mathbb{R}_{+}^{*} \).
Étape 1 : Trouver la solution générale de l’équation homogène associée
L’équation homogène associée est : \(y’ + \frac{2}{t}y = 0\).
On résout cette équation en trouvant la solution générale \(y_h\) :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ y_h(t) &= Ce^{-\int \frac{2}{t} dt}, \ C \in \mathbb{R} \\
y_h(t) &= Ce^{-2\ln|t|}, \ C \in \mathbb{R} \\
y_h(t) &= C\frac{1}{t^2}, \ C \in \mathbb{R}
\end{align*} \)
Étape 2 : Déterminer une solution particulière
On sait que la solution particulière a la forme : \(y_p(t) = f(t)e^{-\int \frac{2}{t} dt}, \ \forall t \in \mathbb{R}_{+}^{*}\).
Étape 3 : Calculer la dérivée de \(y_p\)
La dérivée de \(y_p\) est :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ y_p'(t) &= f'(t)e^{-\int \frac{2}{t} dt} – f(t)\frac{2}{t}e^{-\int \frac{2}{t} dt} \\
&= f'(t)e^{-2\ln|t|} – \frac{2f(t)}{t^2}
\end{align*} \)
Étape 4 : Substituer \(y_p\) et \(y_p’\) dans l’EDO1 initiale
En substituant \(y_p\) et \(y_p’\) dans l’EDO1 initiale, on obtient les équivalences suivantes sur \( \mathbb{R}_{+}^{*} \) :
\( \begin{align*}
&f'(t)e^{-2\ln|t|} – \frac{2f(t)}{t^2} + \frac{2}{t}\left(f(t)e^{-2\ln|t|}\right) = t^2 \\
\Leftrightarrow &f'(t)e^{-2\ln|t|} = t^2 \\
\Leftrightarrow &f'(t)\frac{1}{t^2} = t^2
\end{align*} \)
Étape 5 : Isoler \(f'(t)\)
En isolant \(f'(t)\), on a :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ f'(t) &= t^4
\end{align*} \)
Étape 6 : Trouver \(f\)
On intègre \(f’\) pour trouver \(f\) :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ f(t) &= \int t^4 dt \\
f(t) &= \frac{t^5}{5} + C_1, \ C_1 \in \mathbb{R}
\end{align*} \)
Étape 7 : La solution particulière
La solution particulière est \(y_p(t) = f(t)e^{-\int \frac{2}{t} dt}\), donc :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ y_p(t) = \left( \frac{t^5}{5} + C_1 \right)\frac{1}{t^2}, \ C_1 \in \mathbb{R}
\end{align*} \)
Étape 8 : La solution générale
La solution générale de l’équation différentielle est la somme de la solution générale de l’équation homogène \(y_h\) et de la solution particulière \(y_p\), c’est-à-dire :
\( \begin{align*}
\forall t \in \mathbb{R}_{+}^{*}, \ y(t) &= y_h(t) + y_p(t) \\
&= \frac{C}{t^2} + \left( \frac{t^5}{5} + C_1 \right) \frac{1}{t^2}, \quad (C,C_1) \in \mathbb{R^2}
\end{align*} \)
Voilà, tu sais maintenant tout sur la résolution des équations différentielles d’ordre 1 à coefficients non constants. J’espère que cet exemple t’a permis d’intégrer le chemin classique menant à la résolution. Je t’invite à t’entraîner sur d’autres exercices pour le comprendre encore mieux.
Résolution au second degré
La résolution d’équations différentielles d’ordre 2 à coefficients non constants commence à dépasser de très loin le programme de Maths appliquées. Néanmoins, si tu vises les Parisiennes, connaître cette méthode de résolution te donnera un gros avantage sur tes concurrents si ce type de problème est posé au concours.
Soit \(I\) un intervalle de \( \mathbb{R} \).
Une équation différentielle d’ordre 2 à coefficients non constants se présente ainsi :
\[ (E) :\ a(t)y^{\prime \prime}(t) + b(t)y'(t) + c(t)y(t) = d(t), \ \text{d’inconnue} \ y \in \mathcal{A}(I, \mathbb{R}) \]
N.B. : Ici, (a,b,c) sont trois fonctions continues sur I à valeur dans \( \mathbb{R} \).
La démarche sera la suivante :
Étape 1 : Déterminer une solution \(f_h\) de l’équation homogène associée (évidente ou donnée par l’énoncé).
Étape 2 : Premier changement de variable. On pose \( y = u \times f_h \), avec \( u \in \mathcal{A}(I, \mathbb{R}) \ \) qui est une fonction \(C_1 \ \text{sur} \ I \).
Étape 3 : On injecte notre changement de variable dans \((E)\). On obtient alors quelque chose de la forme \((E) : (af)u^{\prime \prime} + (2af’ + b)u’ = d \). Attention : On parle toujours bien de fonctions ici.
Étape 4 : Deuxième changement de variable. On pose \( z = u’\), et on obtient quelque chose de la forme \((E) : (af)z’ + (2af’ + b)z = d \).
Étape 5 : On est sur une équation différentielle d’ordre 1 à coefficients non constants, que tu sais maintenant résoudre. On résout donc \((E)\) et on détermine \( u = \int z(t) dt, \ \text{puis enfin} \ y = u \times f \).
Un exemple concret
Pour bien comprendre cette méthode un peu fastidieuse, résolvons \((E) : x^{2}y^{\prime \prime}(x) – 2y(x) = 5x^{3}, \quad \text{d’inconnue } y \in \mathcal{A}(\mathbb{R}_{+}^{*}, \mathbb{R}) \)
On repend les notations de la section précédente (notamment pour \(u\) et \(z\))
Étape 1 : L’énoncé donne que \( f_h : \begin{cases} \mathbb{R}_{+}^{*} \to \mathbb{R} \\ x \mapsto x^{2} \end{cases} \ \) est solution de \(E_H\) : \( x^{2}y^{\prime \prime} – 2y = 0 \)
Étape 2 : On pose, \( \forall x \in \mathbb{R}_{+}^{*}, y(x) = u(x) \times x^{2} \), et on observe que :
\( \forall x \in \mathbb{R}_{+}^{*}, y'(x) = u'(x)x^{2} + 2xu(x) \)
\( \forall x \in \mathbb{R}_{+}^{*}, y^{\prime \prime}(x) = u{\prime \prime}(x)x^{2} + 4xu'(x) +2u(x) \)
Étape 3 : On injecte dans \((E)\) et on a \((E) : x^{3} \times (u{\prime \prime}(x)x + 4u'(x)) = 0 \)
On tente de résoudre cette équation, et on se retrouve avec l’équivalence suivante (car \( f_h \) est définie sur \( \mathbb{R}_{+}^{*}) \) :
\( \begin{align*}
x^{3} (u{\prime \prime}(x)x + 4u'(x)) = 0 \\
\Leftrightarrow (u{\prime \prime}(x)x + 4u'(x)) = 0
\end{align*} \)
Étape 4 : On pose \( z = u’ \). On a donc \((E) : z'(x)x + 4z(x) = 5x^{4} \)
Ceci revient à étudier \((E) : y’ + \frac{1}{x}y = 5x^{3} \quad \text{d’inconnue } y \in \mathcal{A}(\mathbb{R}_{+}^{*}, \mathbb{R}) \). Or, tu sais maintenant faire ça !
Je te laisse donc poursuivre l’étude à l’aide de la variation de la constante, tout comme je l’ai fait pour le premier exemple.
Conclusion
Tu sais maintenant tout sur les équations différentielles d’ordre 1 et d’ordre 2 à coefficients non constants. C’est un des aspects les plus poussés que tu puisses voir sur les équations différentielles. Il est certain que bien intégrer ces concepts démontrera que tu es prêt(e) à faire face à toutes les éventualités au concours en ce qui concerne les équations différentielles.
Pour continuer à te préparer aux concours, tu peux également retrouver nos autres ressources mathématiques ici.