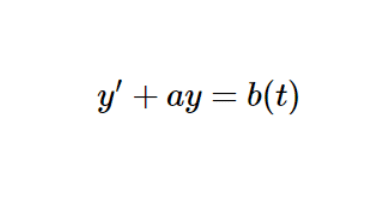Absentes des programmes des ECE/ECS, les équations différentielles font leur grand retour dans le cursus mathématiques appliquées. Cette notion est donc à maîtriser sur le bout des doigts.
Mais qu’est-ce qu’une équation différentielle ?
Une équation différentielle est une équation qui relie une fonction à ses dérivées. Cette fonction est l’inconnue, que l’on note généralement \( y \), et dépend d’une variable, fréquemment notée \( t \) ou \( x \).
Elle permet de décrire comment une quantité change en fonction d’une autre, comme la vitesse d’un objet qui dépend du temps. Ces équations sont utilisées pour modéliser des phénomènes variés, comme la croissance des populations, le mouvement des objets ou les changements de température.
Il existe différents types d’équations différentielles et, ainsi, différentes méthodes pour les résoudre.
Les équations différentielles du premier ordre
Les équations différentielles du premier ordre sont les équations de la forme \[ y’ + ay = b(t) (E)\]
où \( b \) est une fonction continue sur un intervalle \( I \) et \( t \in I \).
L’équation homogène associée à \( (E) \) est \( y’ + ay = 0 (E_{0}) \).
Les solutions de \( (E_{0}) \) sont toutes les fonctions \( g(t) = Ce^{-at}\), où \( C \in \mathbb{R}\).
Les solutions de \( (E)\) sont la somme des solutions de \( (E_{0}) \) et d’une solution particulière de \( (E)\) .
Si \( b \) est une constante, la solution particulière l’est également.
Si \( b \) n’est pas une constante, le sujet guide l’étudiant dans sa recherche.
Les équations différentielles du second ordre
Les équations différentielles du second ordre sont les équations de la forme \( y” + ay’ + by = c(t) (E)\)
où \( c\) est une fonction continue sur un intervalle \( I \) et \( t \in I \).
L’équation homogène associée à \( (E) \) est \( y” + ay’ + by = 0 (E_{0}) \).
L’équation caractéristique de \( (E) \) est \(r^{2} + ar + b = 0 (E_{c}) \).
Si \( (E_{c}) \) admet une unique solution sur \( I \) notée \( r_{0} \), alors les solutions de \( (E) \) sur \( I \) sont toutes les fonctions de la forme :
\[ g(t) = (At + B) e^{-r_{0}t} \]
Si \( (E_{c}) \) admet deux solutions sur \( I \) notées \( r_{1} \) et \( r_{2} \), alors les solutions de \( (E) \) sur \(I \) sont toutes les fonctions de la forme :
\[ g(t) = Ae^{-r_{1}t} + Be^{-r_{2}t} \]
Les solutions de \( (E)\) sont la somme des solutions de \( (E_{0}) \) et d’une solution particulière de \( (E)\) .
Si \( c \) est une constante, la solution particulière l’est également.
Si \( c \) n’est pas une constante, le sujet guide l’étudiant dans sa recherche.
La trajectoire
La trajectoire d’une équation différentielle \( (E)\) sur\( I \) est de l’ensemble \(\{ (t, y(t)) \mid t \in I \}\). Elle correspond à la représentation graphique des fonctions solutions.
On peut obtenir une trajectoire unique en imposant des conditions initiales du type \( y(t_{0}) = y_{0}\)
S’il s’agit d’une équation différentielle du premier ordre, il faudra une condition initiale pour obtenir une unique trajectoire.
S’il s’agit d’une équation différentielle du second ordre, il faudra deux conditions initiales pour obtenir une unique trajectoire.
On appelle trajectoire d’équilibre toute trajectoire associée à une solution constante.
Une trajectoire converge si \( y(t) \) possède une limite finie en \(+\infty\).
Résoudre un système différentiel linéaire à coefficients constants
Soit \( I \in \mathbb{R} \).
On appelle système différentiel linéaire homogène à coefficients constants un système de la forme :
\[
(S) \begin{cases}
x’_1(t) = a_{11}x_1(t) + a_{12}x_2(t) + \dots + a_{1n}x_n(t) \\
\vdots \\
x’_n(t) = a_{n1}x_1(t) + a_{n2}x_2(t) + \dots + a_{nn}x_n(t)
\end{cases}
\]
où \( t \in I\) et \(x_1, \dots, x_n \) sont n fonctions de la variable \(t\), dérivables sur \(I\), et \(a_{11}, \dots, a_{nn} \) sont \(n^2\) réels.
Le but de la résolution de ce système est de trouver les fonctions \(x_1, \dots, x_n\).
Étape 1
Réécrivons le système sous forme matricielle :
On pose pour tout \(t \in I\) :
\[
X(t) = \begin{pmatrix}
x_1(t) \\
x_2(t) \\
\vdots \\
x_n(t)
\end{pmatrix}
\quad \text{et} \quad
X'(t) = \begin{pmatrix}
x’_1(t) \\
x’_2(t) \\
\vdots \\
x’_n(t)
\end{pmatrix}
\]
Et
\[
A = \begin{pmatrix}
a_{11} & \dots & a_{1n} \\
\vdots & \ddots & \vdots \\
a_{n1} & \dots & a_{nn}
\end{pmatrix}
\]
Alors, le système \((S)\) peut s’écrire \(X'(t) = AX(t)\).
Attention : les étapes suivantes sont possibles uniquement si A est diagonalisable !
Étape 2
On diagonalise \(A\) afin de l’écrire sous la forme :
\(A = PDP^{-1}\), où \(D = \begin{pmatrix} \lambda_1 & 0 \\ 0 & \ddots & 0 \\ 0 & 0 & \lambda_n \end{pmatrix} \)
\(D\) est une matrice diagonale qui contient les valeurs propres de \(A\) sur sa diagonale.
\(P\) est une matrice inversible composée des vecteurs propres associés aux valeurs propres de \(A\), organisés en colonnes (attention à prendre le même ordre que pour D !)
Étape 3
On pose \(Y(t)=P^{-1}X(t)\)
On obtient, par dérivation, \[\begin{align}
Y'(t) & = P^{-1}X'(t) \\
& = P^{-1}AX(t) \\
& = P^{-1}APP^{-1}X(t)
\end{align} \]
On a alors : \(Y'(t) = DY(t)(*)\), car \(D=P^{-1}AP \)
Soit \(Y(t) = \begin{pmatrix} y_{1}(t) \\ \vdots \\ y_{n}(t)\end{pmatrix}\)
\(
X'(t) = AX(t) \Leftrightarrow Y'(t)= DY(t)
\)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{pmatrix} y’_{1}(t) \\ \vdots \\ y’_{n}(t) \end{pmatrix} = \begin{pmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{pmatrix} \begin{pmatrix} y_{1}(t) \\ \vdots \\ y_{n}(t) \end{pmatrix}
\)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{cases} y’_{1}(t) = \lambda_{1} y_{1}(t) \\ \vdots \\ y’_{n}(t) = \lambda_{n} y_{n}(t) \end{cases}
\)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{cases} y_{1}(t) = C_{1}e^{\lambda_{1}t} \\ \vdots \\ y_{n}(t) = C_{n}e^{\lambda_{n}t} \end{cases}
\)
\(\forall i \in I, y_i(t) = C_i e^{\lambda_i t}\) , où \(\forall i \in I, C_{i} \in \mathbb{R}\)
On a donc \(Y(t) = \begin{pmatrix} C_1 e^{\lambda_1 t} \\ \vdots \\ C_n e^{\lambda_n t} \end{pmatrix}\)
Étape 4
On retrouve \(X(t)\) par \(X(t) = PY(t)\).
Étape 5 (si demandée)
On résout le système par rapport à des conditions initiales imposées.
Il suffit de replacer le \(t\) dans notre système \( X(t) \), puis de résoudre des équations simples afin de trouver les valeurs de \( C_{i} \).
Théorème de Cauchy : en considérant le système \( (S) X'(t) = AX(t) \) et la condition initiale \( X(t_{o}) = X_{0} \) où \(t_{o} \in I \) et \( X_{0} \in \mathbb{R}^{n} \) sont donnés, alors le problème admet une solution unique.
Exemple
Résoudre le système :
\[
\begin{cases}
x'(t) = y(t) + z(t) \\
y'(t) = -x(t) + 2y(t) + z(t) \\
z'(t) = x(t) + z(t)
\end{cases}
\]
Étape 1
Passons à l’écriture matricielle. On obtient :
\[
X'(t) = A X(t)
\]
où
\[
X(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \end{pmatrix}, \quad A = \begin{pmatrix}
0 & 1 & 1 \\
-1 & 2 & 1 \\
1 & 0 & 1
\end{pmatrix}
\]
Étape 2
Diagonalisons A.
N’hésite pas à consulter cet article si tu n’es pas à l’aise avec les méthodes de diagonalisation d’une matrice.
Soit \(\lambda \in \mathbb{R}\),
\(
\lambda \text{ est une valeur propre de A} \Leftrightarrow A-\lambda I = 0
\)
\(
A-\lambda I = \begin{pmatrix}
-\lambda & 1 & 1 \\
-1 & 2 – \lambda & 1 \\
1 & 0 & 1 – \lambda \end{pmatrix}
\)
On utilise la méthode du pivot de Gauss
On fait \(L_{1}\leftrightarrow L_{3}\) :
\[
\begin{pmatrix}
1 & 0 & 1-\lambda \\
-1 & 2-\lambda & 1 \\
-\lambda & 1 & 1
\end{pmatrix}
\]
Puis \(L_{2}\leftarrow L_{2}+L_{1}\) et \(L_{3}\leftarrow L_{3}+\lambda L_{1}\) :
\[
\begin{pmatrix}
1 & 0 & 1-\lambda \\
0 & 2-\lambda & 2 -\lambda \\
0 & 1 & -\lambda^{2} + \lambda + 1
\end{pmatrix}
\]
On effectue une disjonction de cas
Pour \(2 – \lambda \ne 0\), on fait \(L_{2}\leftarrow \frac{1}{(2 -\lambda)L_{2}}\) :
\[
\begin{pmatrix}
1 & 0 & 1-\lambda \\
0 & 1 & 1 \\
0 & 1 & -\lambda^{2} + \lambda + 1
\end{pmatrix}
\]
Ce qui simplifie les calculs de \(L_{3}\leftarrow L_{3}- L_{2}\) :
\[
\begin{pmatrix}
1 & 0 & 1-\lambda \\
0 & 1 & 1 \\
0 & 0 & -\lambda^{2} + \lambda
\end{pmatrix}
\]
On pose \( A_{\lambda} = \begin{pmatrix}
1 & 0 & 1-\lambda \\
0 & 1 & 1 \\
0 & 0 & -\lambda^{2} + \lambda
\end{pmatrix}\)
\begin{align}
\lambda \text{ est une valeur propre de A} & \Leftrightarrow -\lambda^{2} + \lambda = 0 \\
& \Leftrightarrow \lambda (1 – \lambda) = 0 \\
& \Leftrightarrow\lambda = 0 \text{ou} \lambda = 1
\end{align}
Pour \(2 – \lambda = 0\), soit \(\lambda = 2\)
Ainsi \(A – \lambda I = A – 2I\)
\[ A – 2I = \begin{pmatrix}
1 & 0 & -2 \\
0 & 0 & 0 \\
0 & 1 & -1
\end{pmatrix}
\]
On observe que la deuxième colonne est nulle, ainsi le rang de la matrice est inférieur ou égal à 2, donc 2 est une valeur propre de A.
Ainsi, les valeurs propres de A sont \( \fbox {\(0, 1 \text {et} 2\)} \).
On calcule ensuite les espaces propres associés à 0, 1 et 2
Soit \( X = \begin{pmatrix} x \\ y \\ z\end{pmatrix}\),
Pour la valeur propre 0 :
\(
\begin{align}
X \in E_{0} & \Leftrightarrow (A-0I)X = O \\
& \Leftrightarrow \begin{cases} x + z = 0 \\ y + z = 0 \end{cases} \\
& \Leftrightarrow \begin{cases} x = – z \\ y = – z \end{cases} \\
& \Leftrightarrow X \in \text{Vect}\begin{pmatrix} 1 \\ 1 \\ – 1 \end{pmatrix}
\end{align}
\)
Ainsi \( \fbox {\( E_{0} = \text{Vect}\begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix} \)} \)
Pour la valeur propre 1 :
\(
A_{1} = \begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 1 \\
0 & 0 & 0
\end{pmatrix}
\)
\(
\begin{align}
X \in E_{1} & \Leftrightarrow A_{1}X = O \\
& \Leftrightarrow \begin{cases} x = 0 \\ y + z = 0 \end{cases} \\
& \Leftrightarrow \begin{cases} x = 0 \frac{1}{2} x \\ y = – z \end{cases} \\
& \Leftrightarrow X \in \text{Vect}\begin{pmatrix} 0 \\ 1 \\ – 1 \end{pmatrix}
\end{align}
\)
Ainsi \( \fbox {\( E_{1} = \text{Vect}\begin{pmatrix} 0 \\ 1 \\ -1 \end{pmatrix} \)} \)
Pour la valeur propre 2 :
\(
A – 2I = \begin{pmatrix}
-2 & 1 & 1 \\
-1 & 0 & 1 \\
1 & 0 & -1
\end{pmatrix}
\)
\(
\begin{align}
X \in E_{2} & \Leftrightarrow (A-2I)X = O \\
& \Leftrightarrow \begin{cases} -2x + y + z = 0 \\ -x + z = 0 \\ x – z = 0 \end{cases} \\
& \Leftrightarrow \begin{cases} 2x + y + x = 0 \\ x = z \end{cases} \\
& \Leftrightarrow \begin{cases} -x + y = 0 \\ x = z \end{cases} \\
& \Leftrightarrow \begin{cases} y = x \\ x = z \end{cases} \\
& \Leftrightarrow X \in \text{Vect}\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}
\end{align}
\)
Ainsi \( \fbox {\(E_{2} = \text{Vect}\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} \)} \)
A est d’ordre 3 et possède trois valeurs propres, donc \( \fbox {\( \text{A est diagonalisable } \)} \).
On peut alors écrire \(A\) sous la forme \(A=PDP^{-1}\)
avec \(
D = \begin{pmatrix}
0 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 2
\end{pmatrix}
\)
Et \( P = \begin{pmatrix}
1 & 0 & 1 \\
1 & 1 & 1 \\
-1 & -1 & 1
\end{pmatrix}\)
Calculons \( P^{-1}\) en utilisant la méthode du pivot de Gauss. Si tu ne sais pas inverser une matrice, tu peux consulter cet article.
On a : \[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \\
1 & 1 & 1 & 0 & 1 & 0 \\
-1 & -1 & 1 & 0 & 0 & 1
\end{array} \right]
\]
On fait : \( L_{2} \leftarrow L_{2}+L_{1}\) :
\[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \\
0 & 1 & 0 & -1 & 1 & 0 \\
-1 & -1 & 1 & 0 & 0 & 1
\end{array} \right]
\]
Puis \( L_{3} \leftarrow L_{3}+L_{1}\) :
\[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \\
0 & 1 & 0 & -1 & 1 & 0 \\
0 & -1 & 2 & 1 & 0 & 1
\end{array} \right]
\]
Et \( L_{3} \leftarrow L_{3}+L_{2}\) :
\[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \\
0 & 1 & 0 & -1 & 1 & 0 \\
0 & 0 & 2 & 0 & 1 & 1
\end{array} \right]
\]
Puis \( L_{3} \leftarrow \frac{1}{2}L_{3}\) :
\[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \\
0 & 1 & 0 & -1 & 1 & 0 \\
0 & 0 & 1 & 0 & \frac{1}{2} & \frac{1}{2}
\end{array} \right]
\]
Et \( L_{1} \leftarrow L_{1}-L_{3}\) :
\[
\left[ \begin{array}{ccc|ccc}
1 & 0 & 0 & 1 & -\frac{1}{2} & -\frac{1}{2} \\
0 & 1 & 0 & -1 & 1 & 0 \\
0 & 0 & 1 & 0 & \frac{1}{2} & \frac{1}{2}
\end{array} \right]
\]
Ainsi \( \fbox {\( P^{-1} = \begin{pmatrix}
1 & -\frac{1}{2} & -\frac{1}{2} \\
-1 & 1 & 0 \\
0 & \frac{1}{2} & \frac{1}{2}
\end{pmatrix} \) } \)
Étape 3
Posons \(Y(t)=P^{-1}X(t)\)
On obtient, par dérivation, \[\begin{align}
Y'(t) & = P^{-1}X'(t) \\
& = P^{-1}AX(t) \\
& = P^{-1}APP^{-1}X(t)
\end{align} \]
On a alors : \(Y'(t) = DY(t)(*)\), car \(D=P^{-1}AP \)
Soit \(Y(t) = \begin{pmatrix} y_{1}(t) \\ y_{2}(t) \\ y_{3}(t)\end{pmatrix}\)
\(
X'(t) = AX(t) \Leftrightarrow Y'(t)= DY(t)
\)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{pmatrix} y’_{1}(t) \\ y’_{2}(t) \\ y’_{3}(t) \end{pmatrix} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{pmatrix} \begin{pmatrix} y_{1}(t) \\ y_{2}(t) \\ y_{3}(t) \end{pmatrix}
\)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{cases}
y’_{1}(t) = 0 \\
y’_{2}(t) = y_{2}(t)\\
y’_{3}(t) = 2y_{3}(t)
\end{cases}
\)
Soit \( (C_{1}, C_{2}, C_{3}) \in \mathbb{R}^{3} \)
\(
Y'(t)= DY(t) \Leftrightarrow \begin{cases}
y_{1}(t) = C_{1} \\
y_{2}(t) = C_{2}e^{t} \\
y_{3}(t) = C_{3}e^{2t}
\end{cases}
\)
On a donc \(Y(t) = \begin{pmatrix}
C_{1} \\
C_{2}e^{t}\\
C_{3}e^{2t}
\end{pmatrix}\)
Étape 4
Retrouvons \(X(t)\) par \(X(t) = PY(t)\).
\(
X(t) = PY(t) \Leftrightarrow X(t) = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ -1 & -1 & 1 \end{pmatrix} \begin{pmatrix} C_{1} \\ C_{2}e^{t}\\ C_{3}e^{2t} \end{pmatrix}
\)
\(
X(t) = PY(t) \Leftrightarrow X(t) = \begin{pmatrix}
C_{1} + C_{3}e^{2t}\\
C_{1} + C_{2}e^{t} + C_{3}e^{2t} \\
– C_{1} – C_{2}e^{t} + C_{3}e^{2t}
\end{pmatrix}
\)
Donc, la solution du système initial est \[ \fbox {\( \begin{cases}
C_{1} + C_{3}e^{2t}\\
C_{1} + C_{2}e^{t} + C_{3}e^{2t} \\
– C_{1} – C_{2}e^{t} + C_{3}e^{2t}
\end{cases} \)}
\]
N’hésite pas à faire et refaire cet exercice jusqu’à ce que tu aies bien compris et mémorisé les différentes étapes de résolution d’un système d’équations différentielles.
Tu peux ensuite approfondir cette notion grâce à ces articles :
- Six astuces sur les équations différentielles
- Liens entre équations différentielles et systèmes différentiels
Tu peux également approfondir ta maîtrise en te challengeant avec ces articles :
- Résolution de l’équation différentielle logistique (hors programme ECG)
- Les équations différentielles à coefficients non constants (hors programme ECG)
Tu peux retrouver ici le méga-répertoire qui contient toutes les annales de concours et les corrigés. Tu peux également accéder ici à toutes nos autres ressources mathématiques !