Tu veux savoir quelles formules retenir sur les variables à densité et enfin apprendre à tracer des fonctions de répartition et des densités les yeux fermés ? Alors, cet article est tout ce qu’il te faut ! Dedans, tu y trouveras les formules principales à connaître pour les variables à densité, suivies d’illustrations graphiques.
À noter : les examinateurs demandent très souvent de tracer des graphes de fonctions (surtout à l’oral !) et le tracé de densités ou de fonctions de répartition est donc très régulièrement demandé !
Soit \(X\) une variable aléatoire définie sur \( (\Omega, \mathcal{P}
(\Omega), \mathcal{A})\)
Loi uniforme continue
Soit \((a, b) \in \mathbb{R}^2 \)
On dit que \(X\) suit la loi uniforme sur \([a;b]\), noté \(X \hookrightarrow \mathcal{U}([a,b])\) si elle admet pour densité :
\[ f(x) = \begin{cases} \frac{1}{b-a} &\text{si} \; x \in [a;b] \\ 0 &\text{sinon} \end{cases} \]
Représentation graphique :
Espérance et variance
On a alors : \( E(X)=\frac{a+b}2\textrm{ et }V(X)=\frac{(b-a)^2}{12} \)
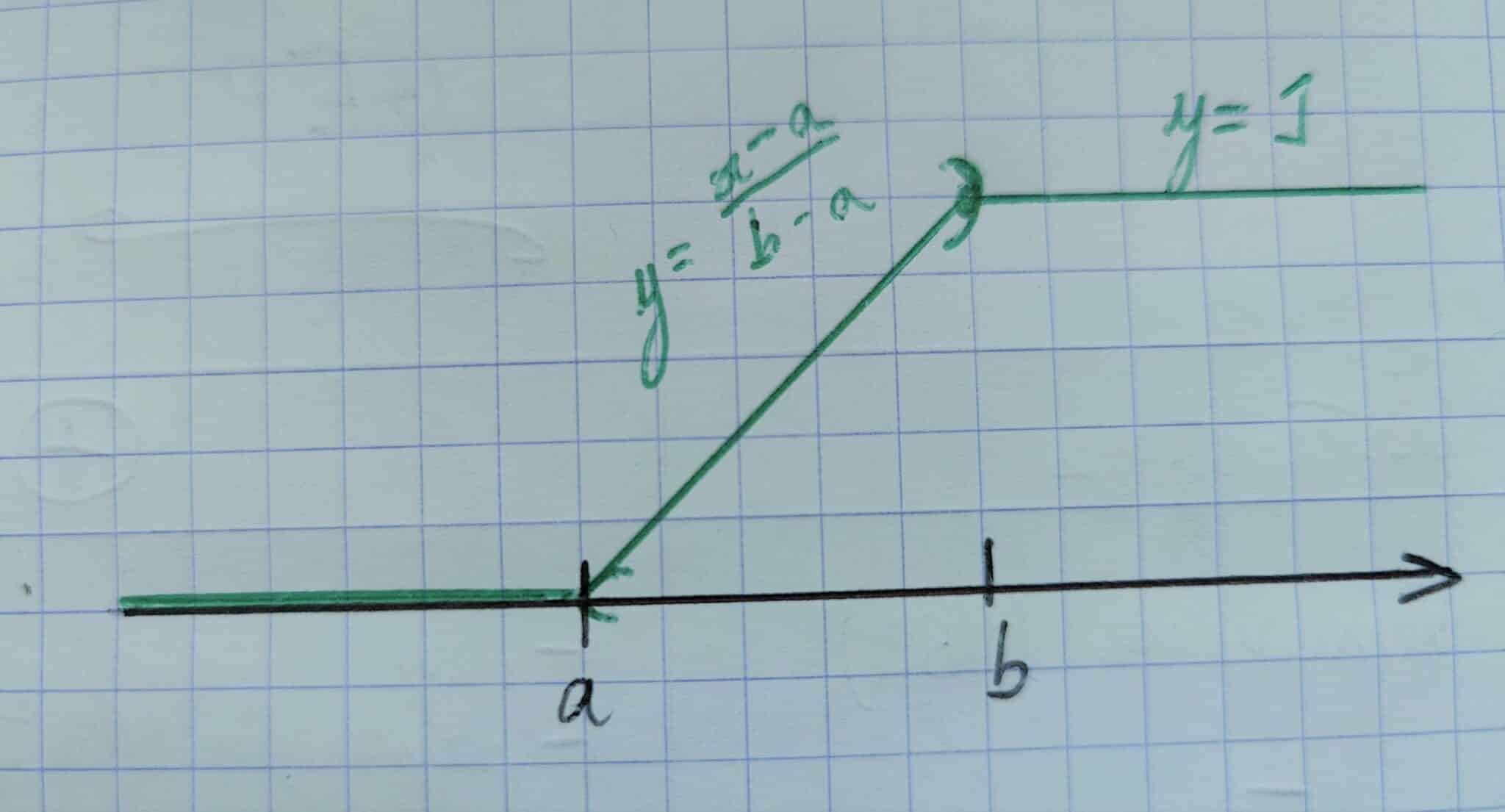
La fonction de répartition est donnée par :
\[ F(x) = \begin{cases} 0 &\text{si} \; x <a \\ \frac{x-a}{b-a} &\text{si} \; x \in [a;b] \\ 1 &\text{sinon} \end{cases} \]
Représentation graphique :
Loi exponentielle
Soit \(\lambda \in \mathbb{R}^{*}_{+} \)
On dit que \(X\) suit une loi exponentielle de paramètre \( \lambda > 0\), ce que l’on note \( X\hookrightarrow \mathcal E(\lambda)\) si elle admet pour densité :
\[ f(x)=\begin{cases} \lambda e^{-\lambda x}&\text{si }x\ge 0\\
0&\text{sinon.}
\end{cases} \]
Représentation graphique :

Espérance et variance
On a alors : \(E(X)=\frac {1}{\lambda}\textrm{ et }V(X)=\frac {1}{{\lambda}^2} \)
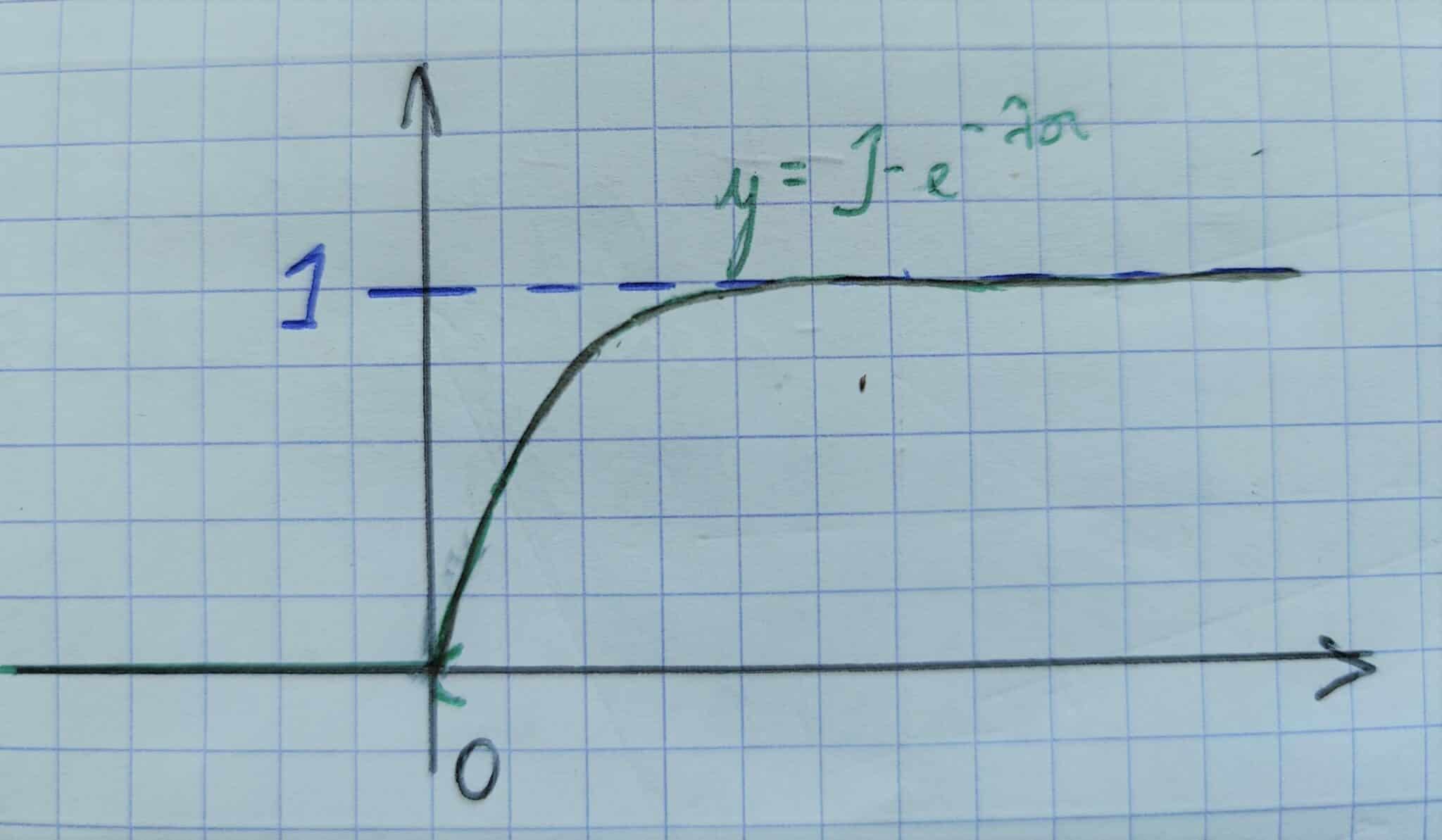
La fonction de répartition est donnée par :
\[ F(x) = \begin{cases} 1-e^{-\lambda x}&\text{si }x\ge {0}\\
0&\text{sinon.} \end{cases} \]
Représentation graphique :
Loi normale centrée réduite
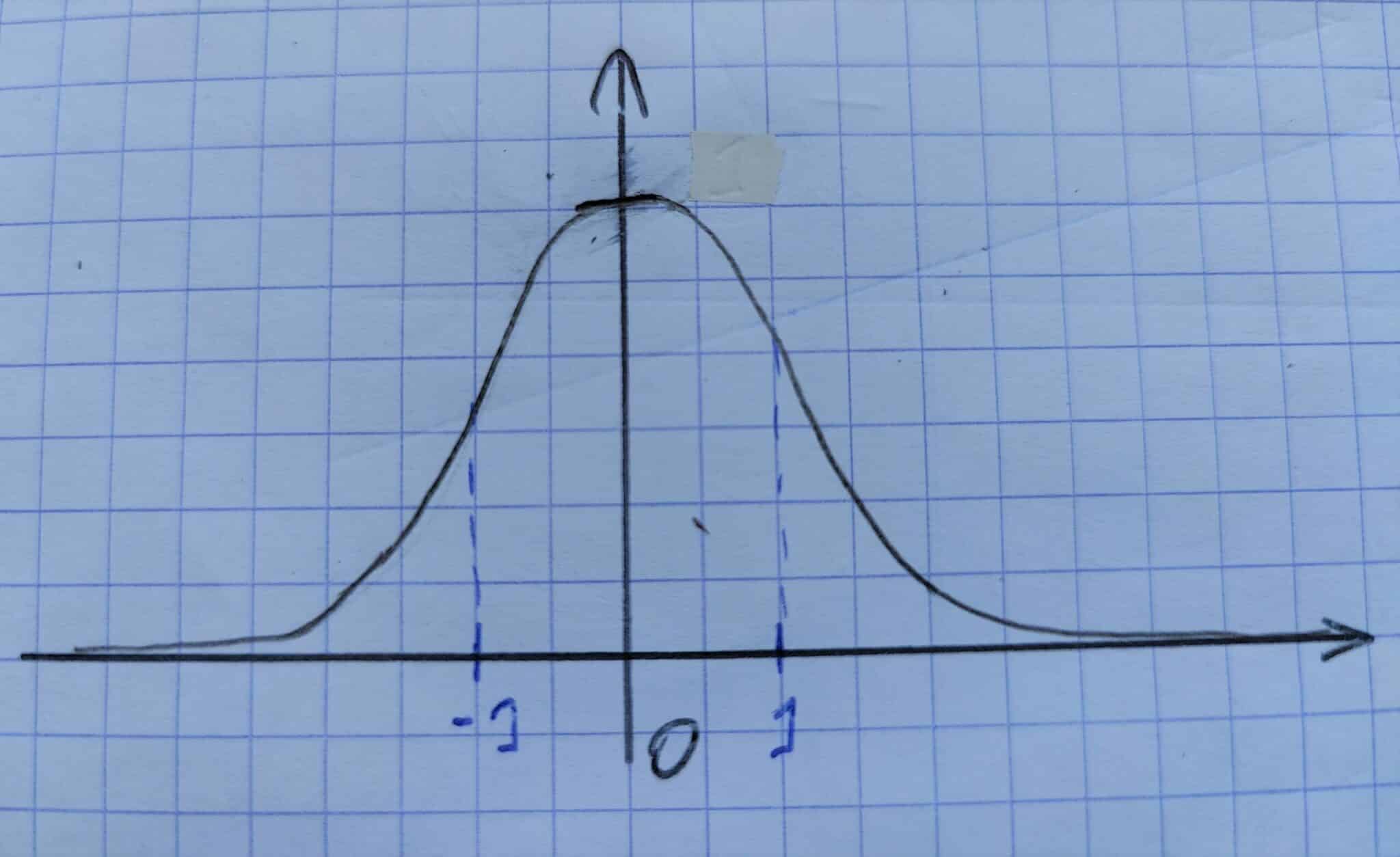
On dit que \(X\) suit une loi normale centrée réduite, ce que l’on note \( X\hookrightarrow \mathcal N(0,1) \) si elle admet pour densité :
\[ f(x)=\frac1{\sqrt{2\pi}}\exp\left(\frac{-x^2}2\right)\]
Représentation graphique :
Espérance et variance
On a alors : \( E(X)=0\textrm{ et }V(X)=1\)
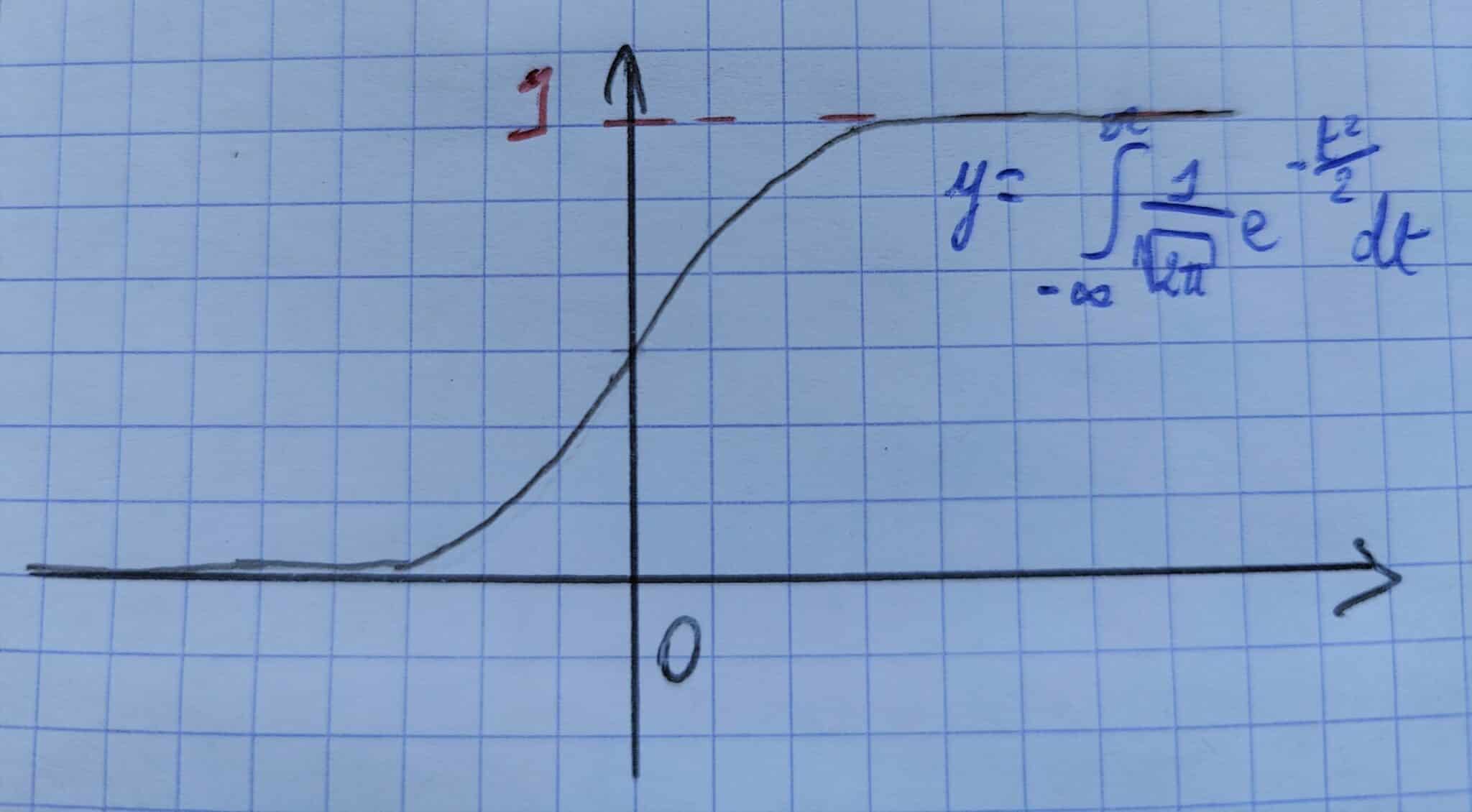
Représentation graphique de la fonction de répartition :
Loi normale – cas général
Soit \( (m, \sigma)\in \mathbb{R}^2 \) (où \( \sigma \ne 0 \) )
On dit que \(X\) suit une loi normale de paramètres \( m \; \textrm {et} \; \sigma\), ce que l’on note \(X\hookrightarrow \mathcal N(m,\sigma^2)\) , si \(X\) admet pour densité :
\[ f(x)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-m)^2}{2\sigma^2}\right)\]
Représentation graphique :
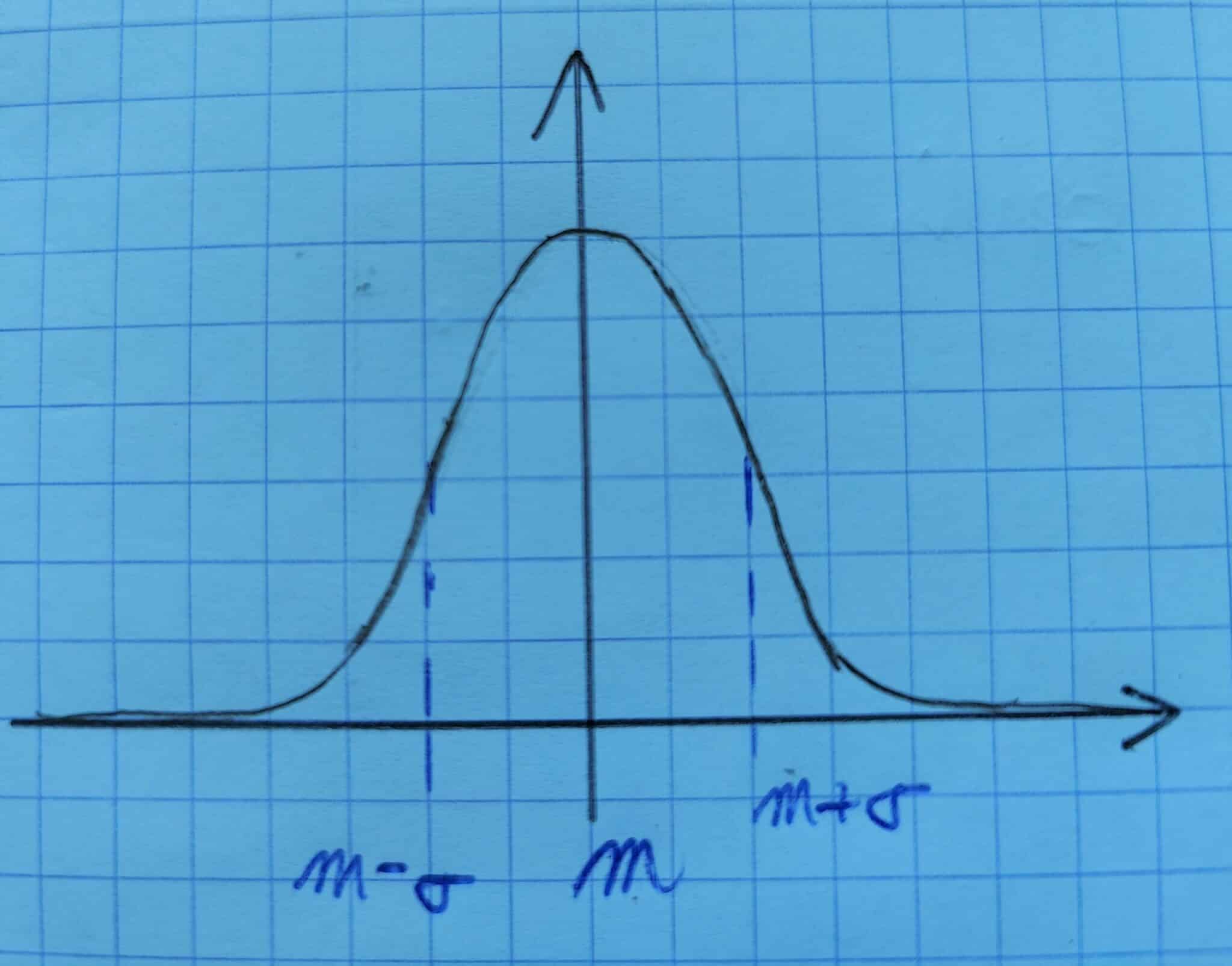
Espérance et variance
On a alors : \( E(X)=m\textrm{ et }V(X)=\sigma^2\).
Représentation graphique de la fonction de répartition :
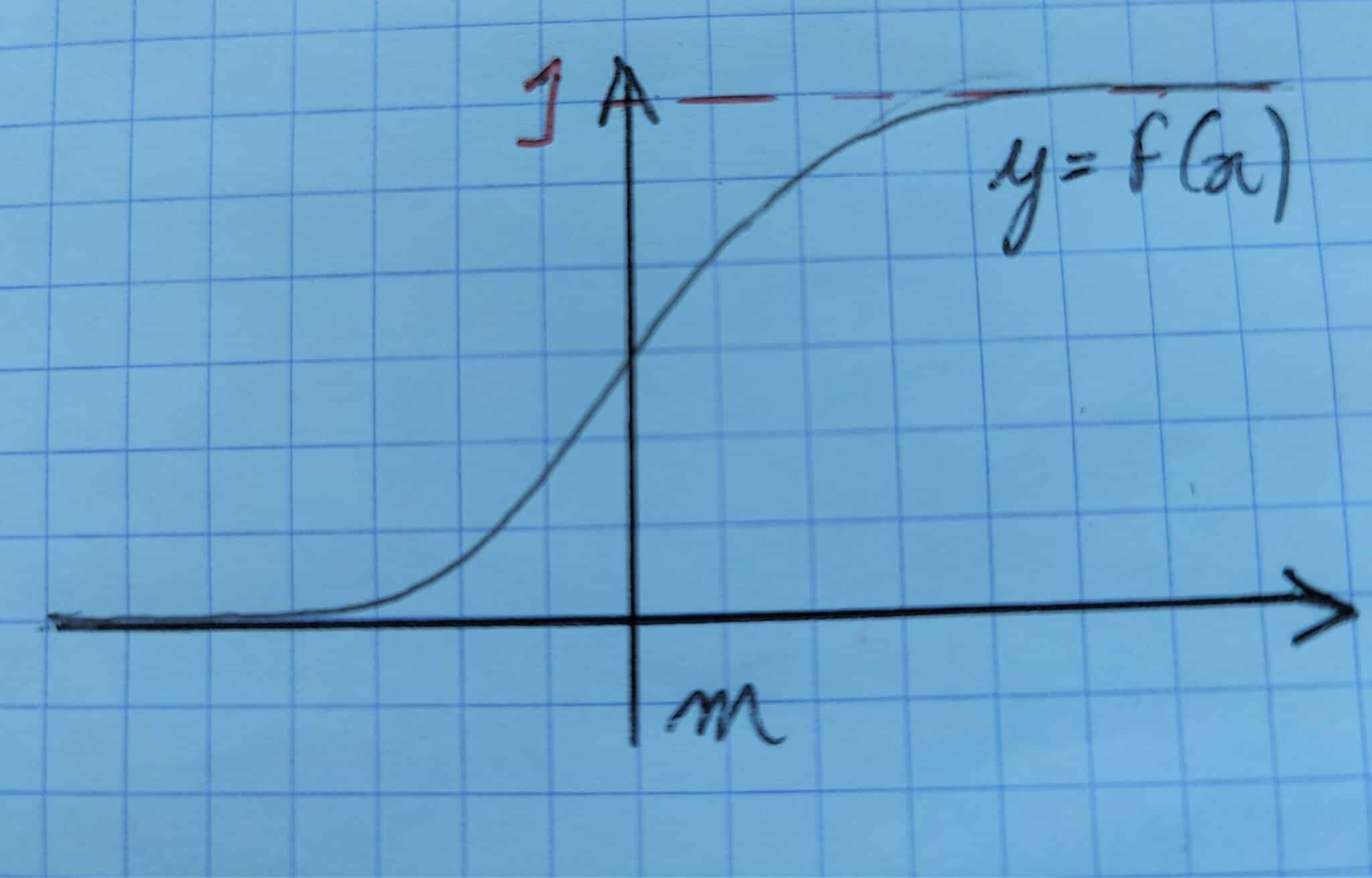
Voilà, tu as maintenant les formules principales sur les variables à densité à portée de main ! Un petit conseil : entraîne-toi à dessiner les graphes des fonctions de densité et des fonctions de répartition pour ne plus avoir de doutes (ça t’aidera aussi à vérifier tes formules). J’espère que cet article t’aura été utile en tout cas !
N’hésite pas à consulter toutes nos ressources en mathématiques ! Et retrouve ici notre fiche express 1.














