Comme tu le sais, l’analyse est une des branches en mathématiques étudiées en classe préparatoire ECG, et est donc importante. Dans cet article, je te propose une fiche récapitulative avec des illustrations graphiques des théorèmes centraux d’analyse que l’on retrouve le plus souvent dans les sujets de concours lorsqu’il s’agit d’étudier des fonctions.
Tu remarqueras que ces théorèmes ne concernent que les fonctions continues sur un intervalle.
Soit \(( a, b) \in \mathbb{R}^2\) tels que \( a< b \).
Pour les fonctions continues sur un segment
Théorème des valeurs intermédiaires
Le théorème des valeurs intermédiaires (c’est-à-dire le TVI) est très important en analyse et revient à de nombreuses reprises.
Énoncé
Soit \(f : [a,b]\to\mathbb R \) une fonction continue. Pour tout réel \( u \) compris entre \( f(a) \) et \( f(b) \), il existe au moins un réel \( c \) compris entre \( a \) et \( b \) tel que \( f(c)=u \).
Illustration
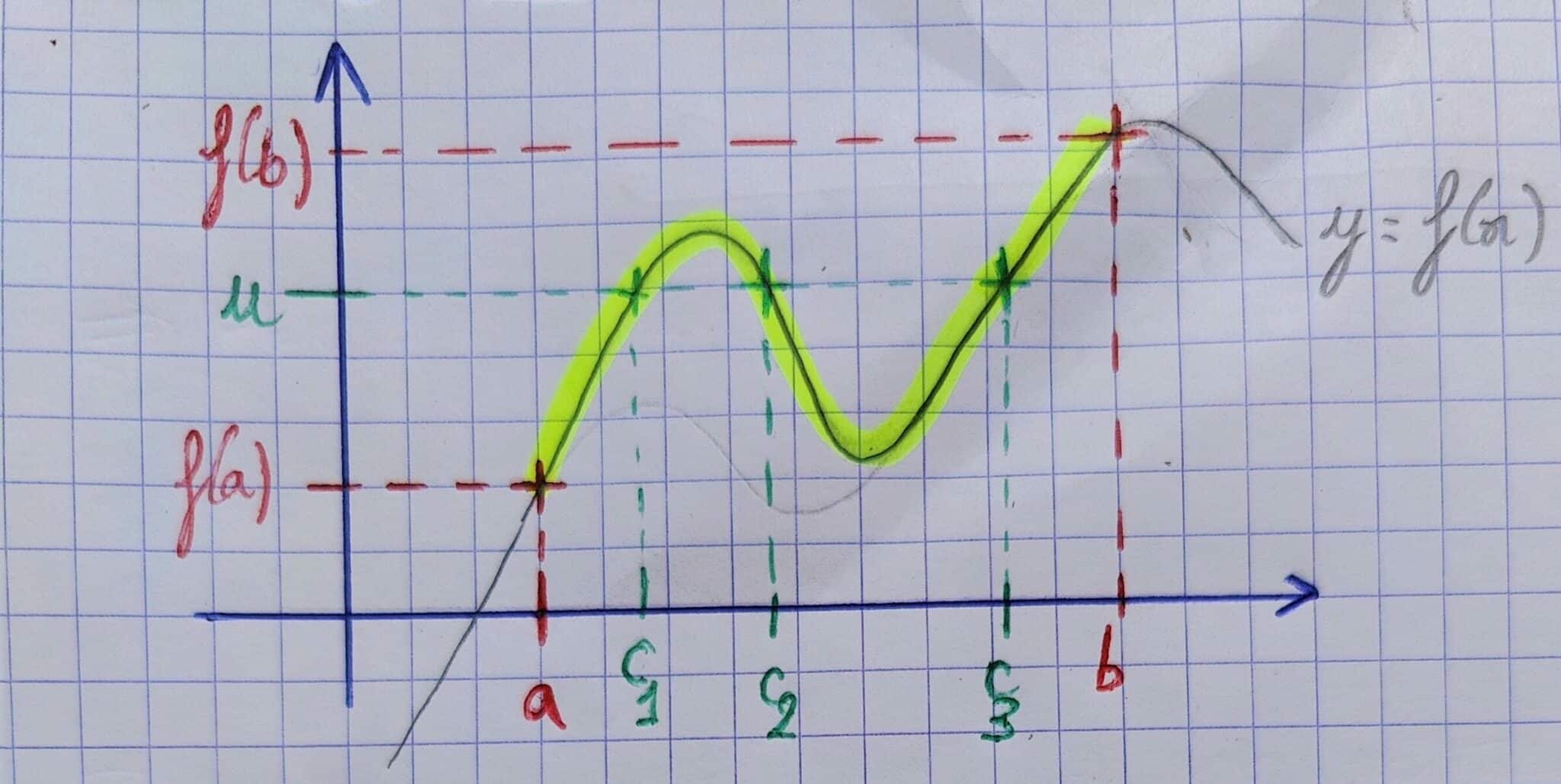
Remarque
Il ne faut pas oublier d’écrire que la fonction est continue sur un intervalle. C’est l’hypothèse clé de ce théorème !
Théorème de la bijection
C’est un corollaire (c’est-à-dire une proposition déduite) du théorème des valeurs intermédiaires. On ajoute ici l’hypothèse que la fonction soit strictement monotone sur l’intervalle \( [a,b] \).
Énoncé
Soit \( f : [a,b]\to\mathbb R \) une fonction continue et strictement monotone. Pour tout réel \( u \) compris entre \( f(a) \) et \( f(b) \), il existe un unique réel \( c \) compris entre \( a \) et \( b \) tel que \( f(c)=u \).
Illustration
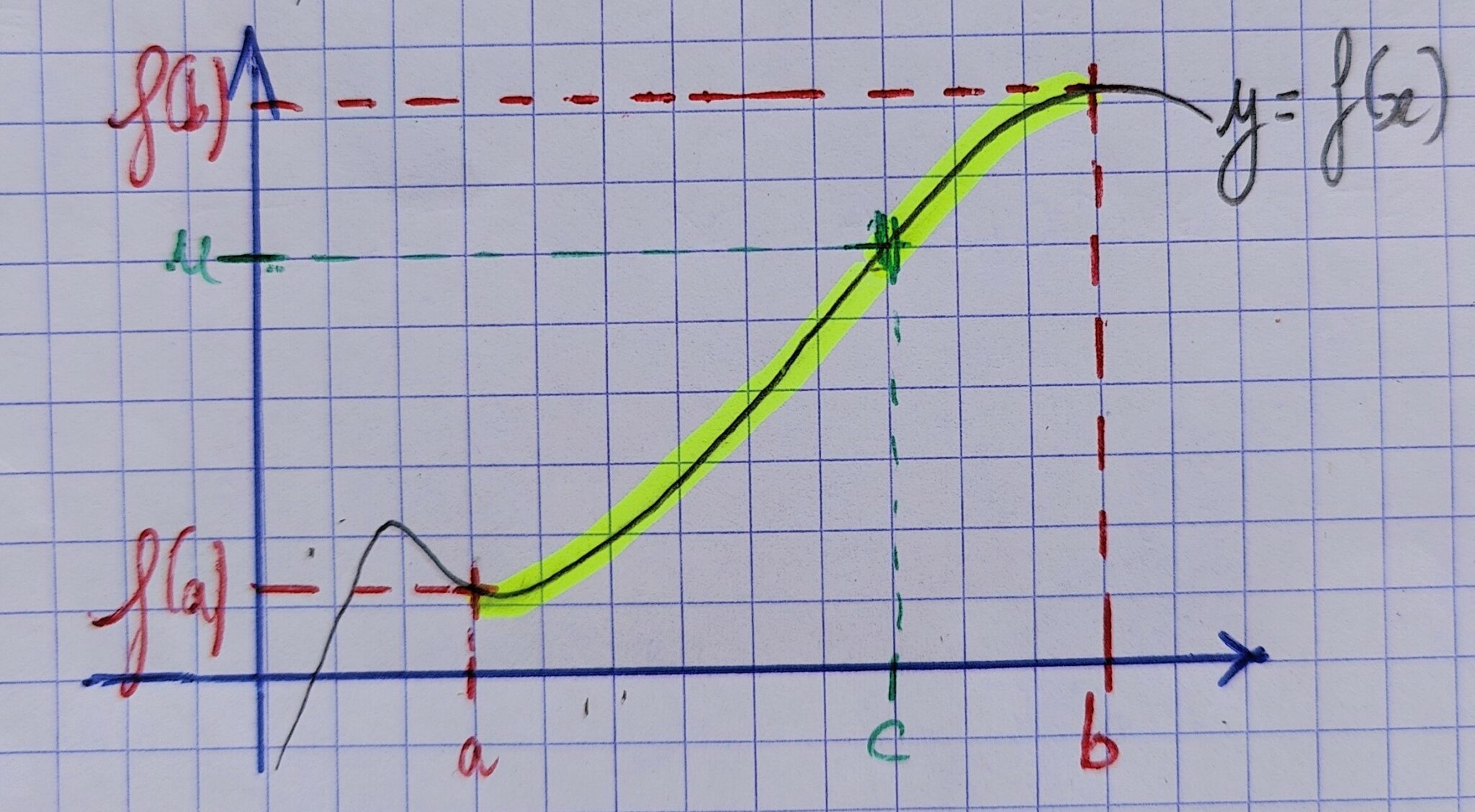
Remarque
Dans les conclusions du théorème, la différence par rapport au TVI est qu’il n’y a qu’un seul antécédent à \( u \) (on le voit dans l’illustration, où il n’y a plus qu’un seul \( c \) qui vérifie \( f(c)=u \) et non pas trois). C’est la stricte monotonie qui induit cela !
Théorème des bornes atteintes
Énoncé
Soit \( f : [a,b]\to\mathbb R \) une fonction continue. Alors \( f \) est bornée et atteint ses bornes.
Remarque
Ici, nous avons bien précisé que la fonction \(f\) est continue sur le segment \([a,b]\). Il s’agit bien d’un segment ! (Un intervalle n’est pas une condition suffisante du théorème.)
Pour les fonctions continues et dérivables sur un intervalle
Théorème des accroissements finis
Énoncé – version égalité
Soit \( f : [a,b]\to\mathbb R \) une fonction continue sur \( [a,b] \) et dérivable sur \( ]a,b[ \). Alors, il existe un \( c \) appartenant à \( [a,b] \) tel que :
\[ f(b)-f(a)=f'( c)(b-a) \]
ou autrement dit :
\[ \frac{f(b)-f(a)}{b-a}=f'( c) \]
Illustration
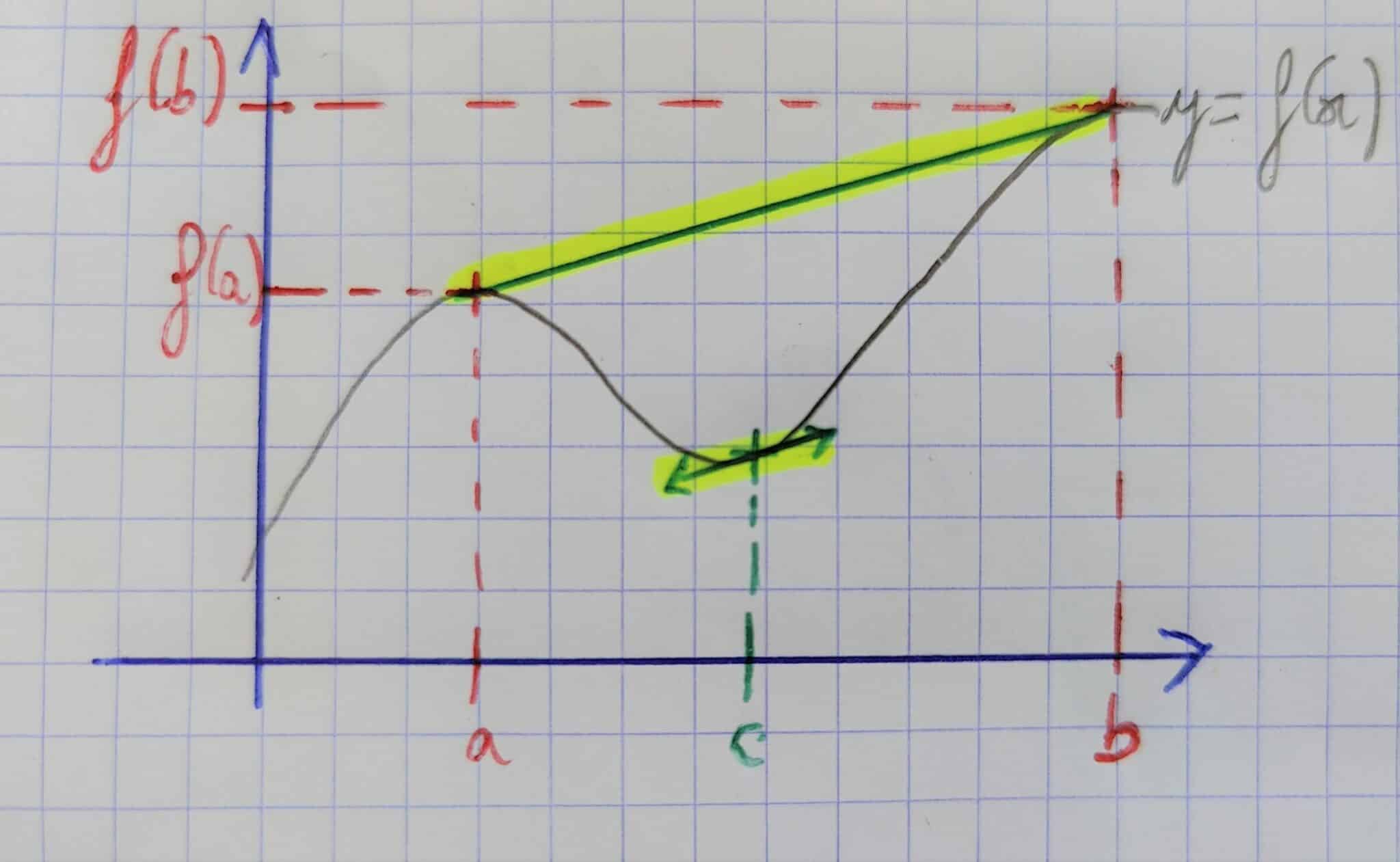
Remarques
- Il ne faut pas oublier l’hypothèse de dérivabilité de la fonction sur un intervalle ouvert (\( ]a,b[ \)).
- Le théorème énonce que la tangente à la courbe en \( c\) a la même inclinaison que la pente de la droite reliant \( f(a) \) à \( f(b) \).
- Le théorème de Rolle est un cas particulier de ce théorème. On ajoute en effet la condition que \( f(a) = f(b) \).
Énoncé – version inégalité
Soit \( f : [a,b]\to\mathbb R \) une fonction continue sur \( [a,b] \) et dérivable sur \( ]a,b[\). On suppose de plus qu’il existe \(M> 0\) tel que pour tout \( t \in ]a,b[ , |f′(t)|≤M\). Alors : \[|f(b)-f(a)|\leq M|b-a|\]
Théorème de Rolle
Énoncé
Soit \( f : [a,b]\to\mathbb R \) une fonction continue sur \( [a,b] \) et dérivable sur \( ]a,b[\). On suppose que \( f(a) = f(b) \).
Alors, il existe \( c \) appartenant à \( [a,b] \) tel que :
\[ f'(c)=0 \]
(En effet, d’après le théorème, on a : \( \frac{f(b)-f(a)}{b-a}= 0 = f'( c) \), car \( f(a) = f(b) \).
Illustration
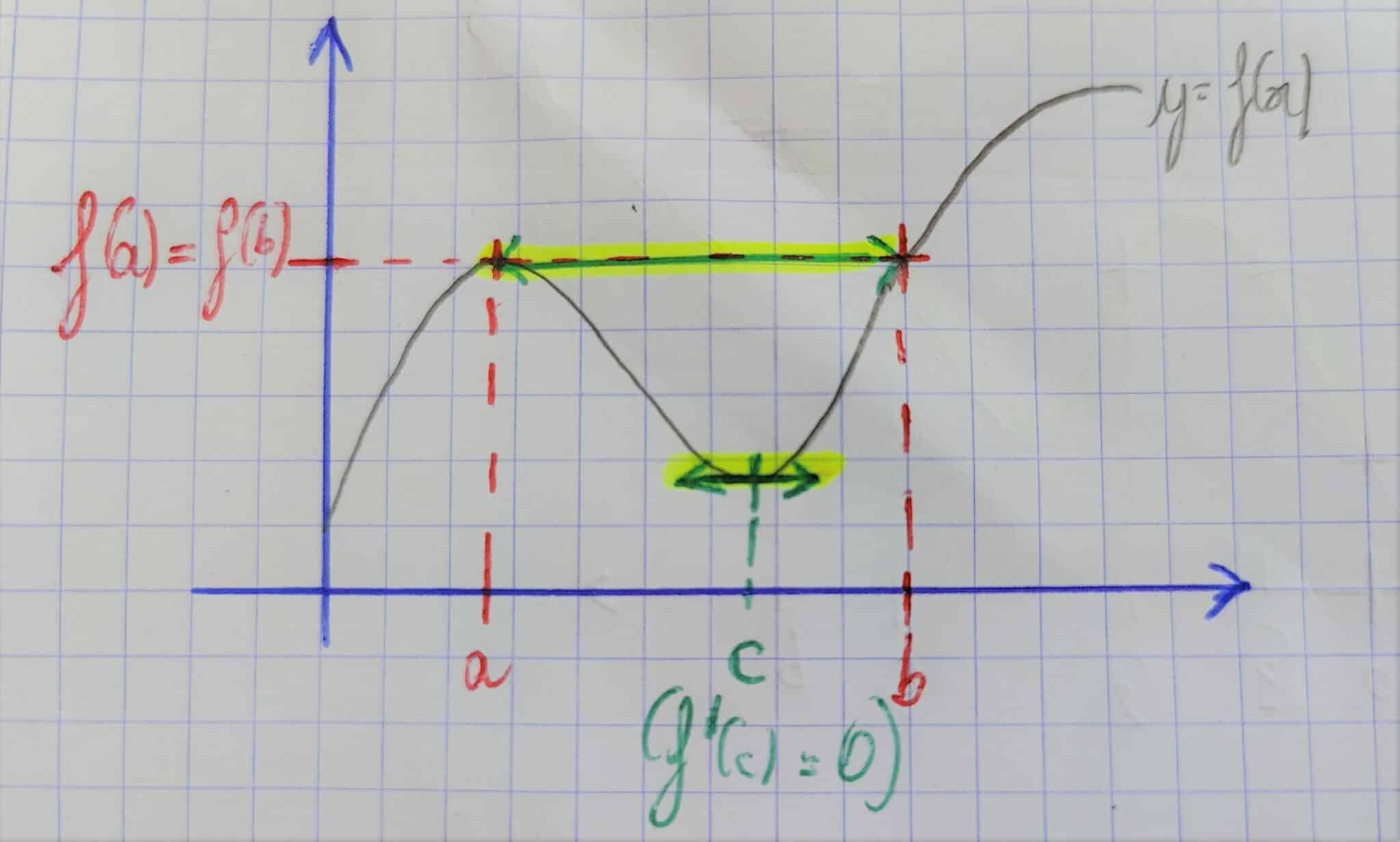
Remarques
- Sur le graphique, on voit bien qu’il s’agit d’un cas particulier du théorème des accroissements finis, puisque l’on parle également de l’inclinaison de la pente (c’est-à-dire du nombre dérivé) en \( c \).
- L’assertion \( f'(c)=0 \) signifie graphiquement que la tangente à la courbe de la fonction \( f\) en \( c \) est horizontale, c’est-à-dire parallèle à l’axe des abscisses.
Conseils généraux
Comme tu l’as sans doute remarqué, presque chaque énoncé de théorème est accompagné d’une illustration graphique. En effet, les concepteurs d’épreuves de concours aiment bien demander de faire des dessins de fonctions, notamment à l’oral.
Par ailleurs, savoir illustrer un théorème permet de mieux le comprendre ! C’est pourquoi je ne peux que t’inviter à t’entraîner à faire des dessins de fonctions pendant l’année ou à illustrer les théorèmes d’analyse, quand cela est possible.
En conclusion, j’espère que cet article t’aura aidé·e à avoir une vue d’ensemble des théorèmes essentiels en analyse fonctionnelle. Je te conseille de recopier cette fiche sur papier, ou une fiche équivalente, dans laquelle tu mets l’énoncé des théorèmes, accompagné de dessins.
Bien sûr, cette fiche n’est pas exhaustive, mais elle peut être très utile pour réviser la veille d’un DS ou d’un jour de concours. 😉
N’hésite pas à consulter toutes nos ressources en mathématiques.













