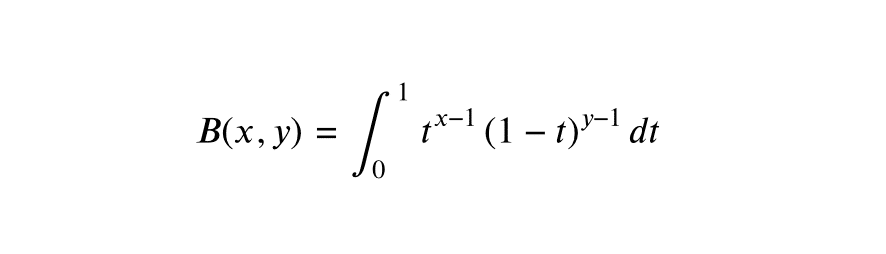La fonction bêta, souvent symbolisée par \(B(x, y)\), est un élément fascinant et crucial dans divers domaines des mathématiques, notamment en calcul intégral, en statistiques et en théorie des probabilités. Cet article vise à étudier cette fonction spéciale, en explorant sa définition, ses propriétés et ses applications, tout en fournissant des exemples pertinents pour les étudiants préparant les épreuves parisiennes et les oraux de mathématiques. Ainsi, bien que cette notion soit hors programme, elle est en relation avec la fonction gamma qui est au programme. Tu pourras donc être amené(e) à la rencontrer dans différentes épreuves.
Définition de la fonction bêta
La fonction bêta, également connue sous le nom de fonction d’Euler de première espèce, est définie par l’intégrale suivante pour tout \(x > 0\) et \(y > 0\) :
\[ B(x, y) = \int_0^1 t^{x-1} (1-t)^{y-1} dt \]
Cette intégrale représente le produit de deux fonctions puissance, dont l’une est élevée à \(x-1\) et l’autre à \(y-1\), avec \(t\) comme variable d’intégration variant de 0 à 1.
Exemple d’application
Considérons le calcul de \(B(2, 3)\) comme un exemple pratique :
\[ B(2, 3) = \int_0^1 t^{2-1} (1-t)^{3-1} dt = \int_0^1 t (1-t)^2 dt \]
En résolvant cette intégrale (en développant et en intégrant le polynôme obtenu), on obtient : \( \displaystyle B(2, 3) = \frac{1}{12} \)
Cet exemple illustre comment calculer la fonction bêta pour des valeurs spécifiques de \(x\) et \(y\), en utilisant la définition intégrale de la fonction.
Les propriétés de la fonction bêta
La fonction bêta possède plusieurs propriétés remarquables qui facilitent son utilisation et son étude.
Propriété de symétrie
\(B(x, y) = B(y, x)\). Cette propriété indique que l’ordre des arguments peut être inversé sans modifier la valeur de la fonction bêta.
Il est important de savoir démontrer cette propriété, car elle peut être l’une des questions posées dans un sujet de concours. Il faut pour cela réaliser un changement de variable dans l’intégrale ci-dessus en posant \(u= 1-t.\)
Autres expressions de la fonction bêta
La fonction bêta ne se limite pas à sa définition intégrale standard. Elle peut être exprimée sous différentes formes intégrales qui peuvent être plus pratiques selon le contexte. Un exemple notable est l’intégrale sur l’intervalle \([0, \displaystyle \frac{\pi}{2}]\) impliquant les fonctions sinus et cosinus :
\[ B(x, y) = 2 \int_0^{\frac{\pi}{2}} \sin^{2x-1}(\theta) \cos^{2y-1}(\theta) d\theta \]
Cette forme résulte d’un changement de variable \( t = \sin^2(\theta) \), et est particulièrement utile dans l’analyse des intégrales trigonométriques.
Une autre expression intéressante de la fonction bêta fait intervenir une intégrale impropre sur \([0, +\infty[\) :
\[ B(x, y) = \int_0^{+\infty} \frac{s^{y-1}}{(1 + s)^{x+y}} ds \]
Ce cas découle du changement de variable \( \displaystyle t = \frac{1}{1 + s} \). Cette forme est souvent rencontrée en théorie des probabilités.
Relation avec des équations fonctionnelles
La fonction bêta satisfait également des équations fonctionnelles qui mettent en lumière des relations intéressantes entre différentes valeurs de ses arguments. Voici quelques-unes de ces relations :
1. La première équation fonctionnelle exprime la relation entre \(B(x, y+1)\) et \(B(x, y)\) :
\[ B(x, y + 1) = \frac{y}{x + y} B(x, y) \]
Cela peut être dérivé directement de la définition de la fonction bêta et offre un moyen récursif de calculer \(B(x, y)\) en termes de \(B(x, y + 1)\). Ce qui peut être utile dans les simplifications algébriques ou encore pour établir une récurrence lorsqu’on travaille avec des entiers naturels.
2. Une autre relation profonde entre les valeurs de la fonction bêta est donnée par :
\[ B(x, y) B(x + y, 1 – y) = \frac{\pi}{x \sin(\pi y)} \]
Cette identité est particulièrement intéressante, car elle relie la fonction bêta à la fonction trigonométrique sinus, illustrant ainsi le lien entre les intégrales et les séries trigonométriques.
3. Enfin, nous avons une équation fonctionnelle qui relie la fonction bêta à elle-même pour des arguments symétriques :
\[ B(x, x) = 2^{1 – 2x} B\left(\frac{1}{2}, x\right) \]
Cela montre que la fonction bêta pour des arguments identiques peut être exprimée par une autre valeur de la fonction bêta. Ce qui peut réduire la complexité des calculs dans certains cas.
Relation avec la fonction gamma
La fonction bêta est étroitement liée à la fonction gamma (\(\Gamma\)), une autre fonction spéciale, par la relation suivante :
\[ \displaystyle B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} \]
Cette relation est particulièrement utile pour calculer des valeurs de la fonction bêta à l’aide de la fonction gamma, bien connue pour ses propriétés et ses valeurs spécifiques. De plus, la symétrie de la fonction bêta peut se déduire de cette relation grâce à la commutativité du produit dans \( \mathbb{R}. \)
Pour illustrer l’utilisation de la fonction bêta, considérons le calcul de \( \displaystyle B(\frac12, \frac12)\), qui a une importance particulière en mathématiques.
\[ B(\frac12, \frac12) = \int_0^1 t^{-\frac12} (1-t)^{-\frac12} dt \]
En utilisant la relation avec la fonction gamma, nous avons :
\[ B(\frac12, \frac12) = \frac{\Gamma(\frac12) \Gamma(\frac12)}{\Gamma(1)} \]
Sachant que \(\Gamma(\frac12) = \sqrt{\pi}\) et \(\Gamma(1) = 1\), nous obtenons :
\[ B(\frac12, \frac12) = \frac{\pi}{1} = \pi \]
Cet exemple montre comment la relation entre les fonctions bêta et gamma peut simplifier le calcul d’intégrales apparemment complexes.
Relation avec des factorielles et les coefficients binomiaux
Lorsque nous traitons avec la fonction bêta pour des entiers strictement positifs \( x \) et \( y \), nous pouvons établir un lien avec les coefficients binomiaux en passant par la fonction gamma.
Étant donné que la fonction gamma d’un entier positif \( n \) est simplement \( (n-1)! \), nous pouvons réécrire la fonction bêta comme :
\[ B(x, y) = \frac{(x-1)! (y-1)!}{(x+y-1)!} \]
Nous pouvons ensuite appliquer la fonction inverse des deux côtés, puis multiplier les deux membres de l’équation par \( \displaystyle \frac{x + y}{xy} \) pour obtenir :
\[ \frac{x + y}{xy} \cdot \frac{1}{B(x, y)} = \frac{x + y}{xy} \cdot \frac{(x+y-1)!}{(x-1)! (y-1)!} \]
En simplifiant, on trouve :
\[ \frac{x + y}{xyB(x, y)} = \frac{(x+y)!}{x! y!} = {{x + y}\choose{x}} \]
Généralisation avec la fonction bêta incomplète
La fonction bêta incomplète est une généralisation intéressante de la fonction bêta standard. Elle est définie pour des valeurs \( a \), \( b \) réelles positives et un paramètre \( x \) dans l’intervalle [0,1] par l’intégrale :
\[ B(x; a, b) = \int_0^x t^{a-1} (1 – t)^{b-1} dt \]
Ainsi, pour \( x = 1 \), la fonction bêta incomplète devient la fonction bêta complète.
Conclusion
La fonction bêta est un outil mathématique puissant et polyvalent, essentiel pour les étudiants qui préparent les épreuves parisiennes. Comprendre sa définition, ses propriétés et ses applications permet non seulement de résoudre des problèmes complexes, mais aussi d’approfondir sa compréhension des mathématiques appliquées.
Pour t’entraîner à manipuler des propriétés similaires à celles que nous venons d’observer, tu peux réaliser ces sujets :
- Maths I 2018 (mathématiques approfondies)
- Maths I 2005 (mathématiques approfondies)
Tu peux retrouver ici toutes nos autres ressources mathématiques !