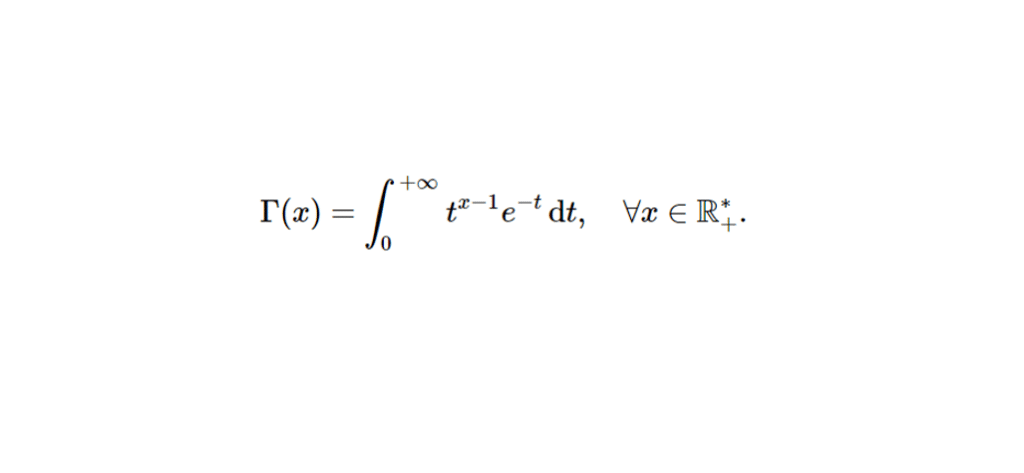La fonction gamma n’est pas au cœur du programme, mais tu dois connaître les démonstrations en lien avec cette fonction. Cela te permettra d’approfondir certaines méthodes et d’être prêt(e) le jour J. Major-Prépa est là pour t’aider.
Définition et propriétés de la fonction gamma
Pour tout réel \(x > 0\), la fonction gamma, notée \(\Gamma(x)\), est définie par l’intégrale suivante :
\[
\Gamma(x) = \int_{0}^{+\infty} t^{x-1} e^{-t} \, \mathrm{d}t, \quad \forall x \in \mathbb{R}_{+}^{*}.
\]
Cette fonction admet trois propriétés à connaître :
- \(\forall x \in \mathbb{R}_{+}^{*}, \Gamma(x+1) = x\Gamma(x)\)
- \(\forall n \in \mathbb{N}^{*}, \Gamma(n) = (n-1)!\)
- \(\Gamma(1/2)= \sqrt{\pi}\)
Les démonstrations de la fonction gamma
Démonstration de l’existence
Cette démonstration est une méthode classique pour prouver la convergence d’intégrales, il faut savoir la refaire !
La fonction \( x \mapsto t^{x-1} e^{-t} \) est continue sur \(\mathbb{R}_{+}^{*}\). Cependant, l’intégrale est impropre en \(0\) et \(+\infty\). Étudions l’intégrale à ses deux bornes.
En 0
Lorsque \( t \to 0 \), nous devons vérifier la convergence de l’intégrale :
\[\int_0^1 t^{x-1} e^{-t} \, \mathrm{d}t.\]
Or, on a :
\[
t^{x-1} e^{-t} \underset{0}\sim t^{x-1}.
\]
Donc,
\[
\int_0^1 t^{x-1} e^{-t} \, \mathrm{d}t \quad \text{et} \quad \int_0^1 t^{x-1} \, \mathrm{d}t
\]
sont de même nature.
Et pour \( x > 0 \) \(\int_0^1 t^{x-1} \, \mathrm{d}t \) converge et vaut \(\frac{1}{x}.\)
Par le critère de comparaison, les fonctions étant positives, l’intégrale\(\int_0^1 t^{x-1} e^{-t} \, \mathrm{d}t\) est aussi convergente.
En \(+\infty\)
Par croissances comparées, on a :
\[
\lim_{t \to +\infty} t^{x-1} e^{-t} = 0
\]
Donc, \(t^{x-1} e^{-t} \underset{t \to +\infty}= o(t^2). \)
Or,
\[
\int_{1}^{+\infty} t^2 \, \mathrm{d}t
\]
converge par le critère de Riemann.
Et par critère de comparaison, les fonctions étant positives, on peut conclure que
\[
\int_{1}^{+\infty} t^{x-1} e^{-t} \, \mathrm{d}t
\]
converge pour \( x \in \mathbb{R}_{+}^{*} \)
On a donc bien prouvé que :
\[
\fbox{\(\int_{0}^{+\infty} t^{x-1} e^{-t} \, \mathrm{d}t \text{ converge.}\)}
\]
Démonstration du point 1
Savoir faire une intégration par parties est une méthode à savoir, cette démonstration te permet de réviser la méthode !
Cette démonstration se fait par intégration par parties en prenant \( u(t) = t^x \) et \( v(t) = -e^{-t} \).
Soit \( x > 0 \) et \( A > 0 \).
\[
\int_{0}^{A} t^x e^{-t} \, dt = \left[ t^x (-e^{-t}) \right]_{0}^{A} – \int_{0}^{A} x t^{x-1} (-e^{-t}) \, dt
\]
\[
= -A^x e^{-A} + x \int_{0}^{A} t^{x-1} e^{-t} \, dt
\]
Or,
\[
\lim_{A \to +\infty} -A^x e^{-A} = 0
\]
Donc,
\[
\lim_{A \to +\infty} \int_{0}^{A} t^x e^{-t} \, dt = x \int_{0}^{+\infty} t^{x-1} e^{-t} \, dt
\]
On a donc bien prouvé que :
\[
\fbox{\(\forall x \in \mathbb{R}_{+}^{*}, \Gamma(x+1) = x \Gamma(x)\)}\]
Démonstration du point 2
Voilà une démonstration relativement facile qui te permet de réviser la méthode pour bien rédiger une récurrence.
Soit \( x > 0 \)
Par récurrence :
Lorsque n = 1
\begin{align}
\Gamma(1) &= \int_{0}^{+\infty} e^{-t} \, dt \\
&= lim_{A \to +\infty}\left[ -e^{-t} \right]_{0}^{A} \\
&= 1 \\
&= 0!
\end{align}
Donc, \[\Gamma(1)= 0!\] et la propriété est initialisée.
Soit \( n > 1 \). Supposons que la propriété soit vraie au rang n. Prouvons qu’elle l’est encore au rang n+1.
On a
\[\begin{align}
\Gamma(n+1) &= n \cdot \Gamma(n) \quad \text{(par la propriété de la fonction gamma)} \\
&= n \cdot (n-1)! \quad \text{(par hypothèse de récurrence)} \\
&= n!
\end{align}\]
Donc, la propriété est héréditaire.
On a bien prouvé que \[\fbox{\(\forall n \in \mathbb{N}^{*}, \Gamma(n) = (n-1)!\)}\]
Démonstration du point 3
Cette démonstration s’adresse à des étudiants qui visent le top 3. Les méthodes utilisées sont souvent présentes dans les maths I et maths II. Le changement de variable est plutôt difficile à voir, mais la méthode pour appliquer ce changement doit être connue de tous. Savoir ajouter des constantes pour obtenir une intégrale valant 1 est aussi une méthode à savoir pour les plus aguerris.
On veut calculer \[ \Gamma(1/2) = \int_{0}^{+\infty}t^{-1/2}e^{-t}\,dt\]
Soit \(A>0\)
On pose le changement de variable, car \(t = \frac{u^2}{2} \), car on veut se ramener à l’intégrale de la densité d’une loi normale centrée réduite, car c’est une intégrale de référence dans le programme. On utilisera aussi \( u = \sqrt{2t}\) et \(dt = udu\)
On a
\[
\begin{align}
\int_{0}^{A} t^{-1/2} e^{-t} \, dt &= \int_{0}^{\sqrt{2A}} \left( \frac{u^2}{2} \right)^{-1/2} e^{-u^2/2} u \, du \\
&= \int_{0}^{\sqrt{2A}} \sqrt{2} e^{-u^2/2} \, du \\
&= 2\sqrt{\pi} \int_{0}^{\sqrt{2A}} \frac{e^{-u^2/2} \, du}{\sqrt{2\pi}}
\end{align}
\]
Or, \[ 2\sqrt{\pi} \int_{0}^{\sqrt{2A}}\frac{ e^{-u^2/2} \, du}{\sqrt{2\pi}} = \sqrt{\pi} \int_{-\sqrt{2A}}^{\sqrt{2A}} \frac{e^{-u^2/2} \, du}{\sqrt{2\pi}}\] par parité de l’intégrande.
Donc, en faisant tendre A vers \(+\infty\) \[ \Gamma(1/2) = \sqrt{\pi} \int_{-\infty}^{+\infty} \frac{e^{-u^2/2} \, du}{\sqrt{2\pi}} = \sqrt{\pi}\] en reconnaissant la loi normale centrée réduite.
On a bien prouvé que\[\fbox{\(\Gamma(1/2) = \sqrt{\pi}\)}\]
La fonction gamma en Python
La fonction gamma est difficile à définir en Python puisque l’intégrale est impropre. Mais on peut utiliser la fonction gamma grâce au module scipy.special :
Il est cependant possible aussi de définir la fonction gamma, mais que sur les entiers naturels. Voici un programme qui utilise la récursivité :
Voici un programme qui utilise le lien avec la loi Gamma et les factorielles :
Il est important de noter que les deux derniers ne marchent que si un entier naturel strictement positif est pris en argument.
La loi Gamma
La fonction gamma permet aussi de définir la loi Gamma. On dit que \(X\) suit une loi Gamma de paramètre \(\nu > 0\) et on note \(X \hookrightarrow \gamma(\nu)\), lorsque la densité de \(X\) est
\[
f(x) =
\begin{cases}
0 & \text{si} \; x \leq 0, \\
\frac{x^{\nu-1} e^{-x}}{\Gamma(\nu)} & \text{sinon}.
\end{cases}
\]
Je te conseille d’approfondir grâce à notre article consacré à la loi Gamma.
La fonction gamma dans les sujets de concours
Bien que la fonction gamma ne soit pas au cœur du programme, elle apparaît beaucoup en probabilité. Voici une liste non exhaustive où la fonction et la loi Gamma apparaissent :
- Maths I HEC 2005 (centré sur la loi Gamma)
- Maths II 1999, 2001, 2006, 2008 et 2010 (centrés sur la loi Gamma)
- EML 2016 et 2024 (centrés sur la fonction gamma seule)
- EDHEC 2014 (centré sur la loi Gamma)
N’hésite pas à consulter toutes nos autres ressources mathématiques.