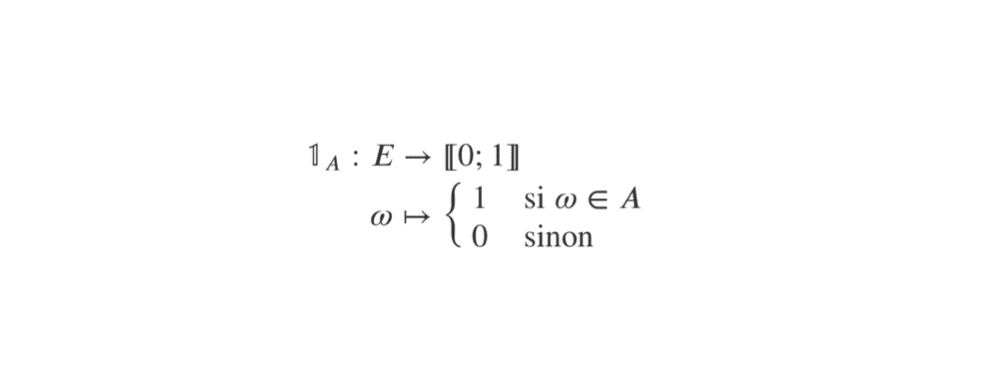Cet article te propose de décortiquer les fonctions indicatrices, une notion assez récurrente dans les sujets de concours. Pour mieux t’aider à la comprendre, tu trouveras ici des exemples, des schémas et une liste des propriétés intéressantes de cette notion afin d’être sensibilisé(e) et non pris(e) au dépourvu le jour J. Cela te simplifiera aussi la tâche pour ficher.
Les notions hors programme se destinent surtout aux candidats qui visent les trois Parisiennes.
La notion de fonction indicatrice expliquée en français
Soit \(E\) un ensemble et \(A\) un sous-ensemble de \(E\). La fonction indicatrice (parfois aussi appelée fonction caractéristique), notée \( \mathbb{1}_{A}\) (x) prend la valeur \(1\) si \(x\) appartient à l’ensemble \(A\) et la valeur \(0\) si \(x\) n’appartient pas à l’ensemble \(A\).
L’application probabiliste de la fonction indicatrice se dénomme la variable indicatrice. Il s’agit d’une variable aléatoire particulière.
L’utilité de la fonction indicatrice
La fonction indicatrice peut être utilisée pour différents objectifs. Elle peut servir à simplifier une fonction existante (qui vaut souvent 0 sur un intervalle donné et est non nulle ailleurs, comme certaines densités de probabilité), en multipliant une indicatrice par une constante.
Cette simplification est notamment faite dans le cadre d’exercices de probabilité.
On utilise également la fonction indicatrice dans le cadre de certaines démonstrations, comme celle de l’inégalité de Markov.
Exemple d’une fonction indicatrice et représentation graphique
Soit \(E = \mathbb{R} \) l’ensemble des réels et \(A = [-2 ; 3] \) un sous-ensemble de \(E\).
\( \mathbb{1}_{A}(x) = \mathbb{1}_{[-2 ; 3]}(x) =
\begin{cases} 1
&\text{si} \; x \in
[-2 ; 3] \\ 0 &\text{sinon}
\end{cases} \)
Par exemple, \( \mathbb{1}_{[-2 ; 3]}(4)=0 \) car \(4\) n’appartient pas à l’intervalle \([-2 ; 3]\).
En revanche, \( \mathbb{1}_{[-2 ; 3]}(1)=1 \) car \(1\) appartient à l’intervalle \([-2 ; 3]\).
Ainsi, on peut retrouver une représentation graphique de la fonction définie ci-dessus qui est la suivante :
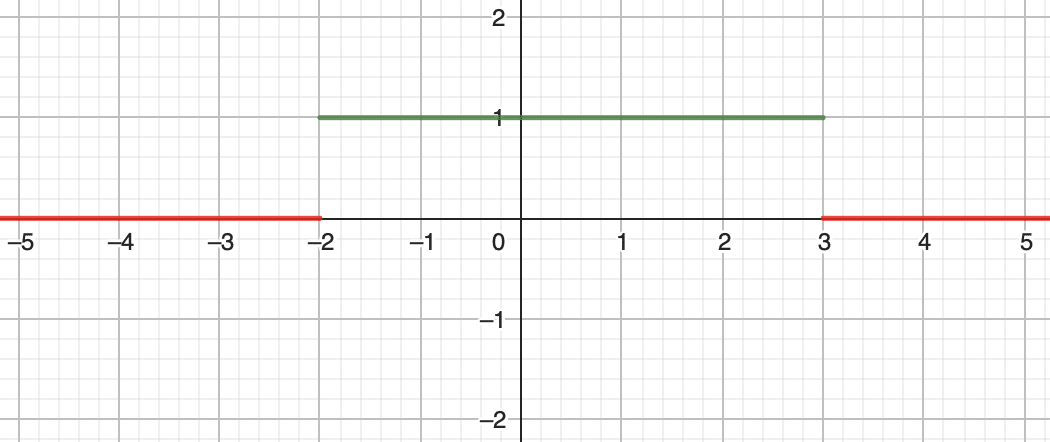
Définition mathématique d’une fonction indicatrice
\(
\begin{align}
\mathbb{1}_{A} &: E \to [\![0 ; 1]\!] \\
&: \omega \mapsto \begin{cases} 1
&\text{si} \; \omega \in
A \\ 0 &\text{sinon} \end{cases} \\
\end{align}
\)
Quelques propriétés sur les fonctions indicatrices et leurs démonstrations
\(A\) et \(B\) désignent ici deux sous-ensembles de \(E\)
- \( \mathbb{1}_{\emptyset}= 0 \)
- \( \mathbb{1}_{\Omega} = 1 \)
- \( ( \mathbb{1}_{A})^{2} = \mathbb{1}_{A} \)
La démonstration est simple, puisque les carrés de \(0\) et de \(1\) (les valeurs prises par la fonction indicatrice) sont respectivement \(0\) et \(1\).
- \( \mathbb{1}_{A} = \mathbb{1}_{B} \Leftrightarrow A=B \)
En effet, si \( \forall x \in \Omega, \mathbb{1}_{A}(x) = \mathbb{1}_{B}(x) \), alors cela signifie que les éléments de \(A\) et de \(B\) sont les mêmes, et donc \(\mathbb{1}_{A} = \mathbb{1}_{B} \Rightarrow A=B\).
Réciproquement, si \(A=B\), alors les éléments de \(A\) et de \(B\) sont les mêmes, et ainsi \( \forall x \in \Omega\), si \(\mathbb{1}_{A}(x)\) prend la valeur \(1\), alors \( \mathbb{1}_{B}(x)\) prendra la valeur \(1\). Ailleurs, ces deux fonctions indicatrices seront nulles et on aura bien \(A=B \Rightarrow \mathbb{1}_{A} = \mathbb{1}_{B} \).
Au total, on a bien \( \mathbb{1}_{A} = \mathbb{1}_{B} \Leftrightarrow A=B \).
- Soient \(A\) et \(B\) tels que \( A \subset B \), alors \( \forall x \in E, \mathbb{1}_{A}(x) \le \mathbb{1}_{B}(x) \).
Démonstration
Premier cas : Soit \( x \in B \) mais \( x \notin A \), alors on a \( \mathbb{1}_{B}(x)=1\) et \( \mathbb{1}_{A}(x)=0 \), ce qui donne bien\( \mathbb{1}_{A}(x) \le \mathbb{1}_{B}(x) \).
Deuxième cas : Soit \( x \in A\), alors comme \(A \subset B\), on a aussi \(x \in B \) et donc \( \mathbb{1}_{A}(x)=1=\mathbb{1}_{B}(x) \), ce qui donne bien à nouveau \( \mathbb{1}_{A}(x) \le \mathbb{1}_{B}(x) \).
Troisième cas : Soit \( x \notin B \), alors comme \(A \subset B\), on a aussi \( x \notin A \) et donc \( \mathbb{1}_{A}(x)=0=\mathbb{1}_{B}(x) \), d’où \( \mathbb{1}_{A}(x) \le \mathbb{1}_{B}(x) \).
Au total, si \( A \subset B \), alors \( \forall x \in E, \mathbb{1}_{A}(x) \le \mathbb{1}_{B}(x) \).
- \( \mathbb{1}_{A \cap B}(x) = \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) \).
Démonstration :
Premier cas : Soit \( x \in B \) et \( x \in A \), alors \( \mathbb{1}_{A \cap B}(x)=1 \) (car \(x \in A \cap B \)), mais aussi \( \mathbb{1}_{B}(x) = 1 \) (car \( x \in B \)) et \( \mathbb{1}_{A}(x) = 1 \) (car \( x \in A \)) donc \( \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x)=1 \), d’où \( \mathbb{1}_{A \cap B}(x) = \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) \).
Deuxième cas : Soit \( x \in B \) mais \( x \notin A \), alors \( \mathbb{1}_{A \cap B}(x)=0 \) (car \(x \notin A\)), et on a \( \mathbb{1}_{B}(x) = 1 \) (car \( x \in B \) ) mais en revanche on a \( \mathbb{1}_{A}(x) = 0 \) (car \( x \notin A \)), ce qui donne donc \( \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x)=0\) et on peut en conclure que \( \mathbb{1}_{A \cap B}(x) = \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) \).
Troisième cas : Soit \( x \in A \) mais \( x \notin B \), on a alors la même démonstration que dans le cas précédent en interchangeant \(A\) et \(B\).
Quatrième cas : Soit \( x \notin B \) et \( x \notin A \), alors on a \( \mathbb{1}_{A \cap B}(x)=0 \) mais aussi \( \mathbb{1}_{B}(x) = 0 \) et \( \mathbb{1}_{A}(x) = 0 \) donc \( \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x)=0 \) et donc \( \mathbb{1}_{A \cap B}(x) = \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) \).
Remarque : On peut voir qu’à chaque fois, on a aussi l’égalité avec \( \min{(\mathbb{1}_{A},\mathbb{1}_{B})} \)
- \( { \mathbb{1}_{A \cup B}(x) =\mathbb{1}_{A}(x) + \mathbb{1}_{B}(x) \text – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) } \).
Démonstration
Premier cas : Soit \( x \in A \) et \( x \in B \), alors on a \( x \in (A \cup B) \), et donc \( \mathbb{1}_{A \cup B}(x)=1\). Par ailleurs, on a \( \mathbb{1}_{A}(x)=1 \) (car \( x \in A \)) et \( \mathbb{1}_{B}(x)=1 \), d’où \(\mathbb{1}_{A}(x) + \mathbb{1}_{B}(x) – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) = 1+1-1 =\mathbb{1}_{A \cup B}(x) \).
Deuxième cas : Soit \( x \in A \) et \( x \notin B \), alors on a \( x \in (A \cup B) \), et donc \( \mathbb{1}_{A \cup B}(x)=1\). Par ailleurs, on a \( \mathbb{1}_{A}(x)=1 \) (car \( x \in A \)) et \( \mathbb{1}_{B}(x)=1 \) (car \( x \notin B \)), d’où \(\mathbb{1}_{A}(x) + \mathbb{1}_{B}(x) – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) = 1+0-0 =\mathbb{1}_{A \cup B}(x) \).
Troisième cas : Soit \( x \in B \) mais \( x \notin A\), on a alors la même démonstration que dans le cas précédent en interchangeant \(A\) et \(B\).
Quatrième cas : Soit \( x \notin B \) et \( x \notin A \), alors \(x \notin (A \cup B)\) et donc \( \mathbb{1}_{A \cup B}(x)=0 \). Par ailleurs, on a \( \mathbb{1}_{A}(x)=0 \) (car \( x \notin A \)) et \( \mathbb{1}_{B}(x)=0 \) (car \( x \notin B \)), d’où \(\mathbb{1}_{A}(x) + \mathbb{1}_{B}(x) – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) = 0+0-0 =\mathbb{1}_{A \cup B}(x) \).
Remarque : On peut voir qu’à chaque fois, on a aussi l’égalité avec \( \max{(\mathbb{1}_{A},\mathbb{1}_{B})} \)
- \( \mathbb{1}_{\overline{A}}(x)=1-\mathbb{1}_{A}(x) \)
Démonstration :
Premier cas : Soit \(x \in A\) (donc \( x \notin \overline{A}\) ), alors on a \( \mathbb{1}_{A}(x)=1\ \) et \( \mathbb{1}_{\overline{A}}(x)=0= 1 – \mathbb{1}_{A}(x) \).
Deuxième cas : Soit \(x \notin A\) (donc \(x \in \overline{A}\), alors on a \( \mathbb{1}_{A}(x)=0 \) et \( \mathbb{1}_{\overline{A}}(x)=1= 1 – \mathbb{1}_{A}(x) \).
- \( \mathbb{1}_{A\backslash B}(x)=\mathbb{1}_{A}(x) – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x) \)
Démonstration
Utilisation des deux propriétés précédentes :
\(
\begin{align}
\mathbb{1}_{A\backslash B}(x) &= \mathbb{1}_{A \cap \overline {B} }(x)\\
&= \mathbb{1}_{A}(x) \times \mathbb{1}_{\overline{B}}(x) \\
&=\mathbb{1}_{A}(x) \times (1 – \mathbb{1}_{B}(x)) \\
&= \mathbb{1}_{A}(x) – \mathbb{1}_{A}(x)\times \mathbb{1}_{B}(x)
\end{align}
\)
- \(\displaystyle \sum_{x \in \Omega } \mathbb{1}_{A}(x) = card(A) \)
En effet, à chaque fois qu’un élément \(x \in A \), la fonction indicatrice prendra la valeur \(1\), sinon elle prendra la valeur \(0\) et cela permettra donc de dénombrer le nombre d’éléments dans A.
Sujet de concours avec la notion de fonction indicatrice
N’hésite pas à consulter toutes nos ressources mathématiques.